
Функции / Линии второго порядка / Линии второго порядка.Построение
.docЛинии второго порядка
Все кривые второго порядка: окружность, эллипс, гипербола и парабола в некоторой системе координат могут быть записаны с помощью уравнения
![]() ,
причем
,
причем ![]()
Если при этом:
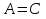 ,
то уравнение задает окружность;
,
то уравнение задает окружность;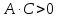 –
уравнение
определяет эллипс;
–
уравнение
определяет эллипс;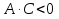 – уравнение
определяет гиперболу;
– уравнение
определяет гиперболу;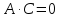 ,
то линия является параболой.
,
то линия является параболой.
В практических задачах встречается параллельный перенос эллипса:
Уравнение
![]() задаёт эллипс с большой полуосью «а»,
малой полуосью «в» и центром симметрии
в точке
задаёт эллипс с большой полуосью «а»,
малой полуосью «в» и центром симметрии
в точке ![]() .
.
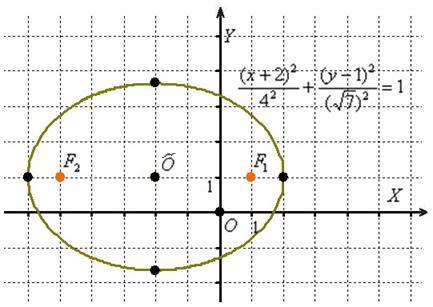
Изобразим
на чертеже эллипс
![]() .
.
Согласно
формуле: ![]() ,
то есть наш подопытный эллипс «переехал»
в точку
,
то есть наш подопытный эллипс «переехал»
в точку ![]() :
:
 Значения
Значения
![]() остались
прежними, а вот фокусы, разумеется,
мигрировали, и формулы их координат
придётся находить с поправкой на
соответствующие сдвиги:
остались
прежними, а вот фокусы, разумеется,
мигрировали, и формулы их координат
придётся находить с поправкой на
соответствующие сдвиги:
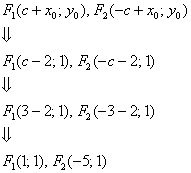
Здесь всё обходится значительно проще, чем при повороте, и если по условию не нужно приводить уравнение к каноническому виду, то лично я предпочту оставить его в виде .
Что делать, если нужно приводить?
«Чайникам»
в большинстве случаев простят фразу:
«Осуществим параллельный перенос
эллипса в начало координат и перепишем
уравнение
в
каноническом виде: ![]() ».
».
Но академический подход предполагает параллельный перенос не самой фигуры, а системы координат!
Поэтому
людям, изучающим высшую математику по
профилю и/или углублённо, гораздо лучше
завернуть примерно следующее: «С помощью
параллельного переноса исходной системы
координат перейдём к новой прямоугольной
системе координат
![]()
с
началом в точке
и
запишем уравнение эллипса в каноническом
виде ![]() ».
».
Задание.
Определить тип линии и построить
![]()
Преобразуем выражение , выделив полные квадраты.
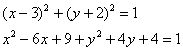
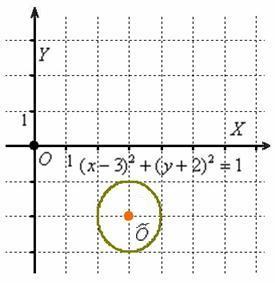
Уравнение
![]() задаёт окружность
радиуса
задаёт окружность
радиуса ![]()
с центром в точке .
Таким образом, в практических задачах часто предварительно нужно выполнить обратное действие – выделить полные квадраты. Данный приём подробно разобран на уроках о геометрических преобразованиях графиков и интегрировании дробей. Хотя следующий простой пример не должен вызвать у вас затруднений даже без отработки данного метода:
Задание. Записать каноническое уравнение гиперболы (x-5)2 + y2 = 5(x-1)2.
Решение. Преобразуем уравнение к каноническому виду.
х2 - 10х + 25 + у2 = 5х2 - 10х + 5, получим: 4х2 - у2 = 20.
Разделим
обе части уравнения на 20:
![]()
Это
каноническое уравнение гиперболы. Из
него видно, что действительная полуось
равна а=![]() ,
а мнимая b=
,
а мнимая b=![]() .
.
