Функции / Линии второго порядка / Задачи с решениями. Кривые второго порядка

Задачи с решениями. Кривые второго порядка.

Написать уравнение окружности с центром в точке C(2, -3) и радиусом, равным 6.

Решение.

По уравнению

(x - a)² + (y - b)² = r²,

полагая в нем a = 2, b = -3, r = 6, сразу имеем (x - 2)² + (y + 3)² = 36, или x² + y² - 4x + 6y - 23 = 0.

Найти координаты центра и радиус окружности x² + y² - x + 2y - 1 = 0.

Решение.

Преобразуем уравнение к виду

(x - a)² + (y - b)² = r².   (1)

Соберем члены, содержащие только x и только y:

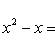
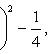
y² + 2y = (y + 1)² - 1.

Заданное уравнение перепишется в виде

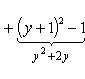
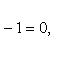
или

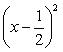
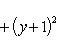
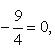
и окончательно в виде

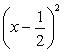
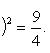
Следовательно, из сравнения с уравнением (1) заключаем, что центр окружности находится в точке  , а радиус равен  .

Составить простейшее уравнение эллипса, зная, что:  а) его полуоси a = 6, b = 4;  б) расстояние между фокусами 2c = 10, а большая полуось 2a = 16;  в) большая полуось a = 12, а эксцентриситет e = 0,5;  г) малая полуось b = 8, а эксцентриситет e = 0,6;  д) сумма полуосей a + b = 12, а расстояние между фокусами  .

Решение.

а) Простейшее уравнение эллипса имеет вид  . Подставляя сюда a = 6, b = 4, получим

б) Имеем 2c = 10; c = 5; 2a = 16; a = 8.

Чтобы написать уравнение эллипса, следует найти малую полуось b. Между величинами a, b и c у эллипса существует зависимость a² - b² = c², или b² = a² - c². В нашем случае b² = 64 - 25 = 39, и уравнение эллипса будет иметь вид

в) a = 12; e = 0,5; известно, что  ; в этой формуле неизвестно c. Для его определения получаем уравнение

отсюда c = 6.

Теперь, зная, что a = 12, c = 6, пользуясь отношением a² - c² = b², найдем, что b² = 144 - 36 = 108; a² = 144.

Уравнение будет  .

г) b = 8; e = 0,6;  , отсюда  . Напишем соотношение a² - c² = b² и подставим в него c = 0,6a; b = 8. Получим a² = 0,36a² = 64; 0,64a² = 64; a² = 100.

Уравнение эллипса будет иметь вид

д) a + b = 12,  .

Для определения уравнения эллипса надо знать a и b. Нам известно, что  ; c² = 18; a² - b² = c².

Поэтому (a + b)(a - b) = 18. Подставляя сюда a + b = 12, найдем, что a - b = 1,5.

Решая систему уравнений

получим, что a = 6,75, b = 5,25. Уравнение эллипса запишется в виде

Найти длины осей, координаты фокусов и эксцентриситет эллипса 4x² + 9y² = 144.

Решение.

Преобразуем это уравнение к простейшему виду  . Разделив обе части заданного уравнения на 144, получим  .

Отсюда заключаем, что a² = 36, b² = 16. Значит, a = 6, 2a = 12; b = 4, 2b = 8. Зная a и b, из соотношения a² - c² = b² найдем c. Подставим a = 6; b = 4 и получим, что  . Координаты фокусов будут   и  . Эксцентриситет эллипса

Составить простейшее уравнение гиперболы, если расстояние между ее вершинами равно 20, а расстояние между фокусами 30.

Решение.

Вершины параболы лежат на ее действительной оси. По условию 2a = 20; 2c = 30. Значит, a = 10; c = 15; a² = 100; c² = 225.

Величины a, b, c у гиперболы связаны соотношением

a² + b² = c²;

отсюда b² = c² - a² = 225 - 100; b² = 125.

Значит, уравнением гиперболы будет

Гипербола проходит через точк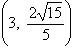и   и  . Найти уравнение гиперболы.

Решение.

Уравнение гиперболы

может быть записано так

b²x² - a²y² = a²b².     (1)

Определению подлежат a² и b². Подставим в это уравнение координаты первой точки и получим

45b² - 12a² = 5a²b².

Подставляя в уравнение гиперболы (1) координаты второй точки, получим

20b² - 9a² = a²b².

Решим систему уравнений

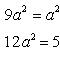
Умножая первое уравнение на 4, а второе на 3 и вычитая из второго первого, получим a² = 5. Подставим a² = 5 в первое уравнение и получим 20b² - 45 = 5b², откуда b² = 3. Подставляя найденные значения a² и b²в (1), получим, что искомое уравнение имеет вид

3x² - 5y² = 15.

Уравнения асимптот гиперболы y = x/2 и y = -x/2, а расстояние между фокусами 2c = 10. Найти уравнение гиперболы.

Решение.

Уравнения асимптот гиперболы имеют вид

Из условия задачи следует, что: 1)   и a = 2b; 2) c = 5. Подставляя в соотношение a² + b² = c² значения a = 2b и c = 5, получим (2b)² + b² = 25; b² = 5; a = 2b, а потому a² = 4b² = 20.

Искомым уравнением гиперболы будет  .

Парабола y² = 2px проходит через точку A(2, 4). Определить ее параметр p.

Решение.

Подставляем в уравнение параболы вместо текущих координат координаты точки A (2, 4). Получаем

4² = 2p*2; 16 = 4p; p = 4.

Составить уравнение параболы, зная, что вершина ее находится в начале координат а расстояние от фокуса до вершины равно 4 единицам длины, а осью симметрии служит ось Ox.

Решение.

Так как осью симметрии параболы служит ось Ox, а вершиной - начало координат, то парабола может быть определена одним из уравнений y² = 2px и y² = -2px. Параметр параболы p есть расстояние от директрисы параболы до фокуса. Расстояние от фокуса до вершины равно половине параметра. Значит, у нас  . Подставляя это значение p в каждое из только что написанных уравнений, получим

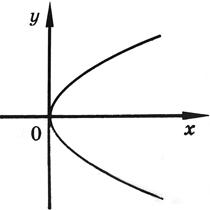
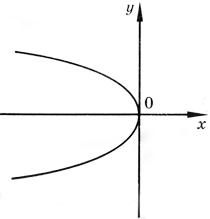
y² = 16x и y² = -16x.

Эскизы парабол указаны на рисунках