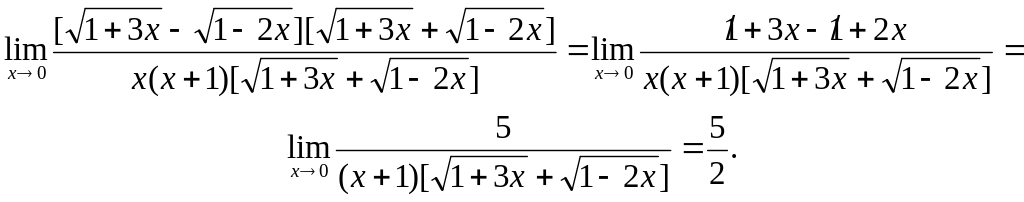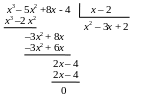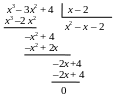Функции / Предел и непрерывность / Пределы вида 0делить на 0 Примеры решения задач

Вычисление пределов функций y = f(x), значение которых в точке при х = х₀ определено f(x) = А не вызывает затруднений:

Затруднения возникают, когда в точке х = х₀ при вычислении значения функции получаем неопределенности вида В этом случае для вычисления пределов нужно преобразовать исходную функцию, чтобы неопределенность исчезла, либо в результате преобразования привести исходную функцию к первому или второму замечательному пределу.

Пример 1.

Вычислить 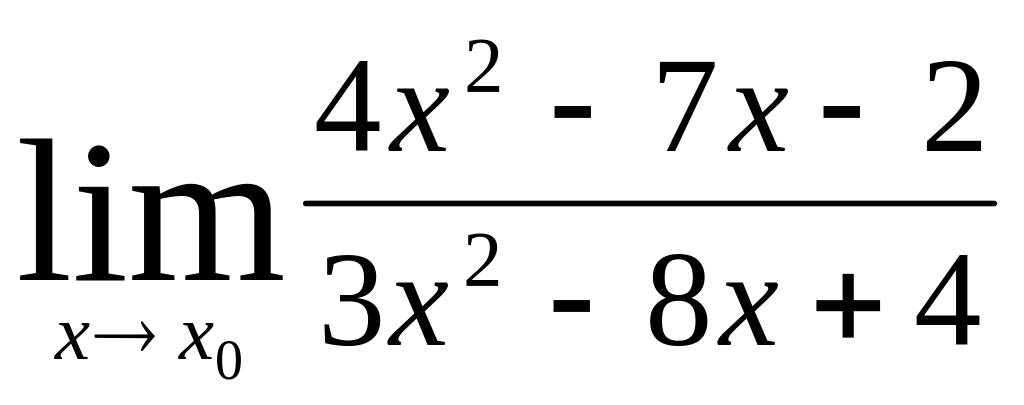при

Решение. Так как определена в точке , то предел функции в точке равен значению функции в этой точке, т. е.

;

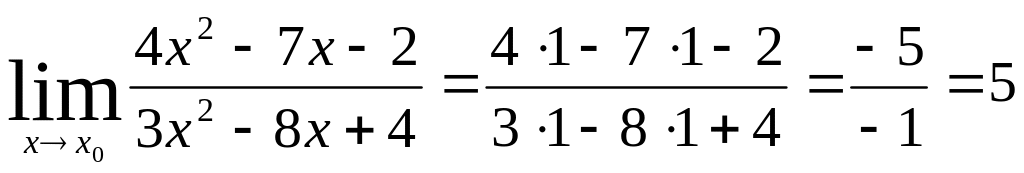Пример 2.

Вычислить при

Решение. В точке функция также определена. Тогда получим:

.

Пример 3.

Вычислить при .

Решение. При получили неопределенность . Для решения разложим числитель и знаменатель на множители, сократим дробь:

; ; ;

.

; ; ;

;

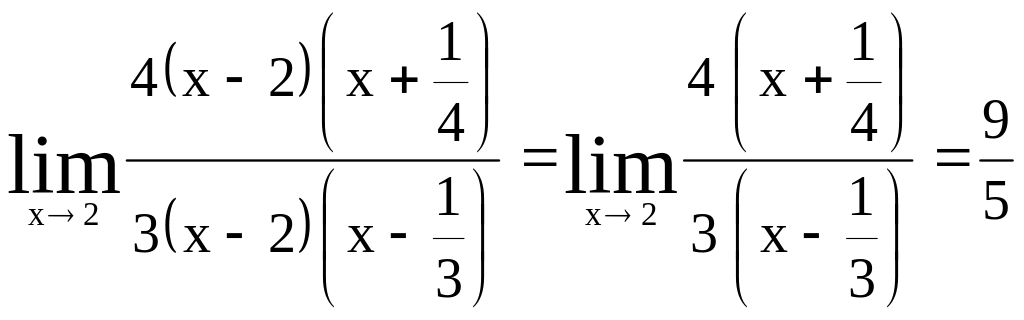После сокращения дроби опять в предел подставляем и вычисляем предел.

Пример 4.

Найти предел:

Решение. .

Избавимся от иррациональности в знаменателе, умножив и разделив дробь на выражение , сопряженное знаменателю, и применим формулу

.

Выделим множитель и сократим на него дробь.

Примечание.

Аналогично избавляются от иррациональности в числителе.

Пример 5.

Вычислить предел:

Решение. При непосредственной подставке х = –1 получаем неопределенность . Для ее исключения проведем преобразование функции:

При х = –1 знаменатель обращаться в ноль за счет сомножителя х + 1. разделим числитель на этот сомножитель:

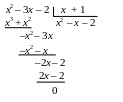
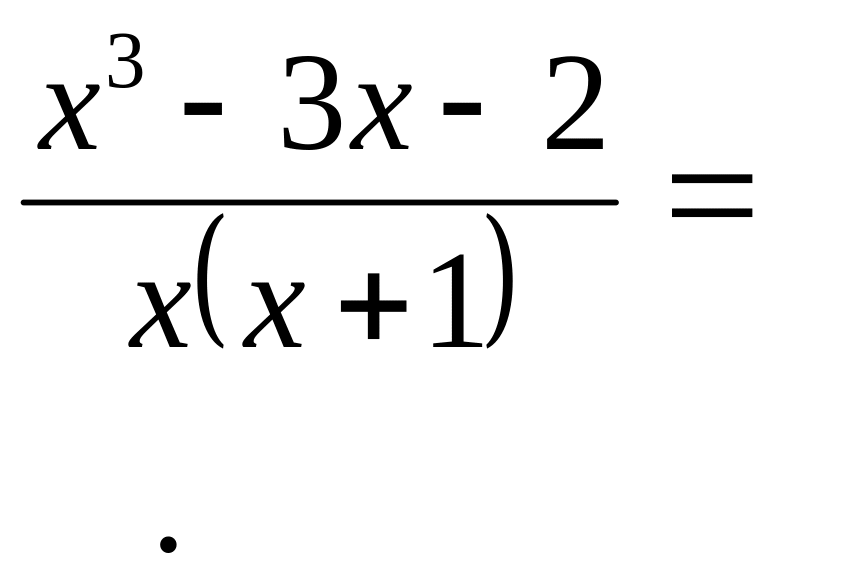
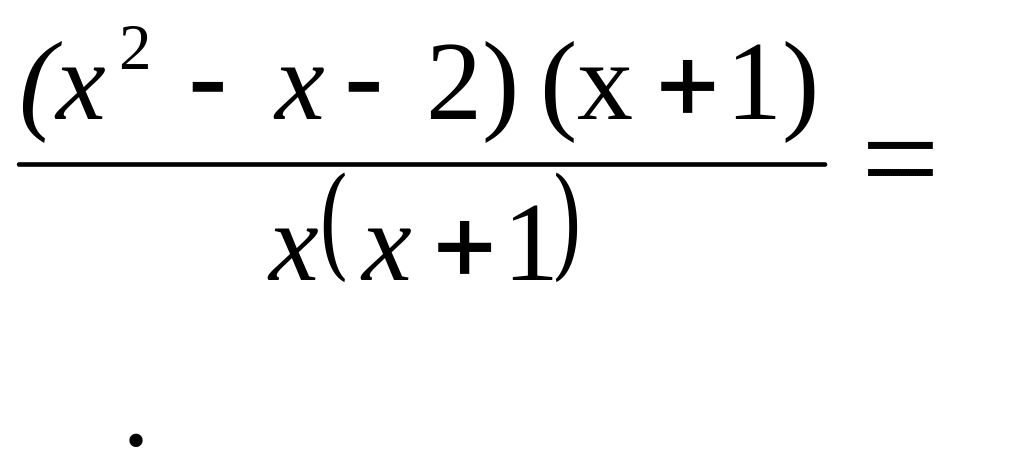
В результате предел преобразуется к виду:

Пример 6.

Вычислить предел:

Решение. При непосредственной подставке х = –2 получаем неопределенность . Для устранения неопределенности разложим числитель и знаменатель на сомножители. Так как и числитель, и знаменатель при х = 2 обращаются в ноль, то они содержат общий сомножитель х – 2. найдем вторые сомножители числителя и знаменателя:

В результате разложения на сомножители числителя и знаменателя предел преобразуется к виду:

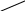
При подстановке х = 2 опять получаем неопределенность . Еще раз разделим числитель и знаменатель на х – 2 и в результате получим:

Пример 7.

Вычислить предел:

Решение. При непосредственной подстановке х = 0 получаем неопределенность . Для ее устранения умножим числитель и знаменатель дроби на выражение, сопряженное числителю, на

В результате мы избавимся от иррациональности в числителе: