Функции / Предел и непрерывность / Исследовать на непрерывность (1)

Задача.

Исследовать на непрерывность, выяснить характер точек разрыва и изобразить графически следующие функции

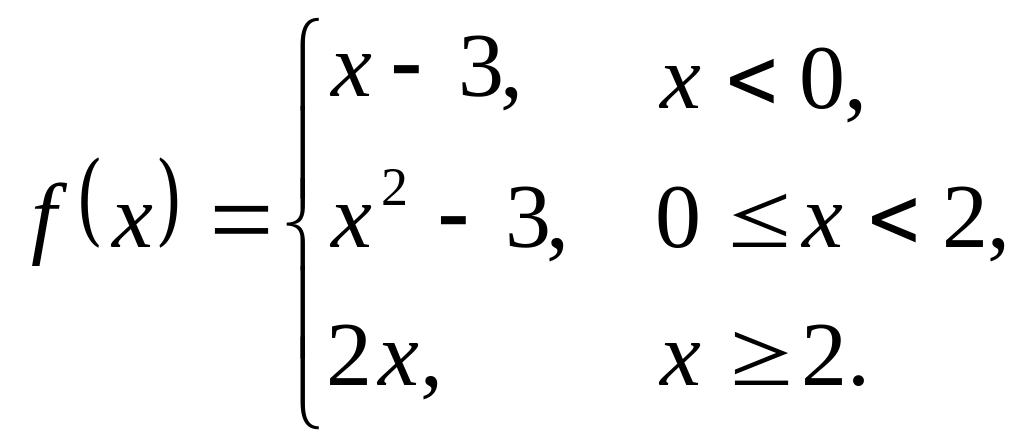
Решение:

а) Построим график данной функции, составляющими которой являются линейная функция , квадратичная функция (на промежутке ) и линейная функция .

4

1

0 2 х

_-3

Исследуем функцию на непрерывность. К точкам, в которых возможно функция терпит разрыв, относятся точки (точки, где функция меняет свое аналитическое задание).

Для того, чтобы функция в точке была непрерывна необходимо и достаточно, чтобы

Проверим это условие для точки :

Условие выполнено, значит, функция в точке непрерывна.

Аналогичным образом исследуем на непрерывность в точке .

Функция в точке терпит разрыв I рода.