Функции / Предел и непрерывность / Замечательные пределы (1)

Замечательные пределы.

При вычислении пределов функций при х → х₀ или х → ∞ часто возникают проблемы из-за того, что функция не определена при х → х₀ (х → ∞).

Первым примером такой функции является функция .

Первым замечательным пределом называется предел этой функции при х → 0:

(1)

Пример 1.

Вычислить предел функции при х → 0.

Решение. Подставляя значение аргумента х = 0 в заданную функцию, видим что функция в заданной точке не определена (имеет неопределенность вида ). Для нахождения предела заданной функции попробуем привести ее к первому замечательному пределу. Используя формулу преобразования тригонометрических функций , получим:

дальнейшие преобразования проведем с использованием основных теорем о пределах.

Второй сомножитель в полученном выражении совпадает с формулой (1). Первый сомножитель так же эквивалентен формуле (1) так как может быть записан в виде: , где z = 2х.

Пример 2.

Найти:

Задание: найти пределы, используя первый замечательный предел и эквивалентность бесконечно малых величин:

=

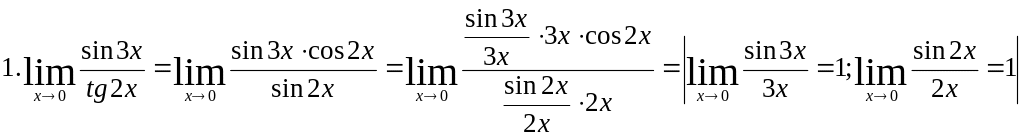2.

3.

4.

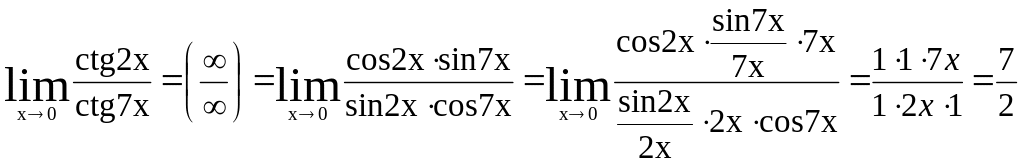
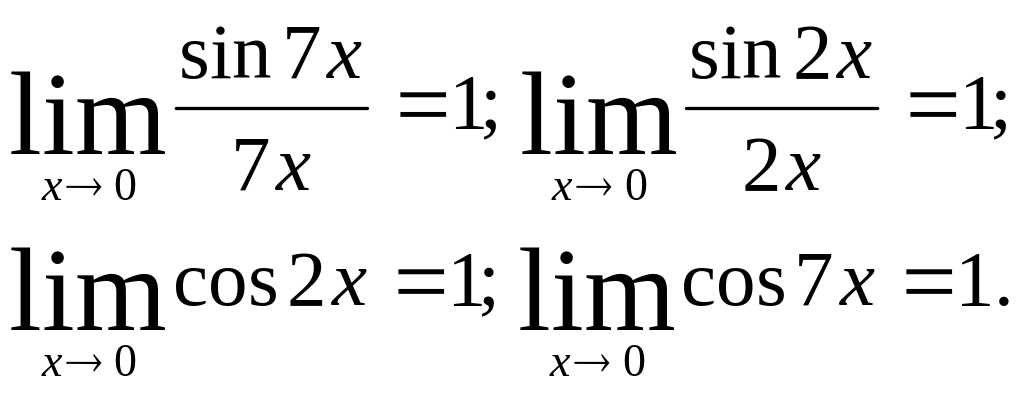
Второй замечательный предел.

Рассмотрим числовую последовательность: .

Если вычислять значения членов последовательности при натуральных значениях номера n числовой последовательности, то получим:

у₁ = 2; у₂ = 2,25; у₃ = 2,37; у₄ = 2,441; у₅ = 2,488; ... ... у₁₀ = 2,59; ... у₅₀ = 2,69; у₁₀₀ = 2,71.

Из приведенных значений видно, что числовая последовательность является монотонной неубывающей. Это обусловлено увеличением показателя степени при увеличении номера n числовой последовательности. Если рассматриваемую последовательность представить (по формуле бинома Ньютона) в виде (n + 1) слагаемых, то можно показать, что эта последовательность ограничена сверху.

Ограничение возрастания рассматриваемой числовой последовательности обусловлено стремлением к единице основания степени при увеличении номера n числовой последовательности.

Данная числовая последовательность имеет предел:

. (2)

Формулу (2) называют вторым замечательным пределом.

Число е в математике еще называют числом Эйлера, неперовым числом. Число е является иррациональным и с точностью до шестой значащей цифры оно равно

е = 2,71828….

Если рассматривать числовую последовательность как значения некоторой функции при x = n, то получим другую запись второго замечательного предела:

(3)

Причем этот предел равен е при х → +∞ и при х → –∞, и формулу (3) можно записать в виде:

(4)

Если в формуле (3) произвести замену независимой переменной (при х → ∞, z → 0) получим еще одну форму записи второго замечательного предела:

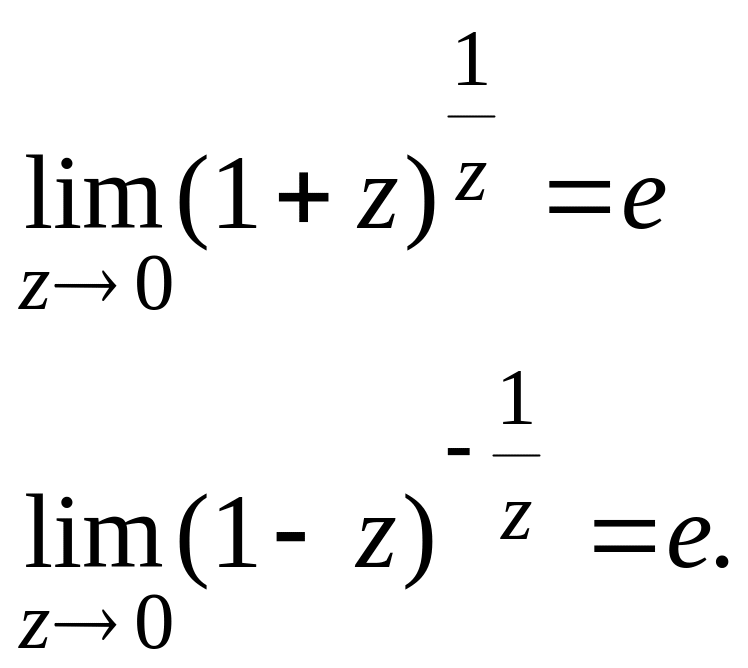(5)

Пример 3.

Вычислить предел функции .

Решение. Для решения приведем данный предел ко второму замечательному пределу в записи формулы (4).

1. Умножим числитель и знаменатель дроби на 2 и числитель почленно разделим на знаменатель:

.

2. Сделаем замену переменной и решим по формуле (5):

.
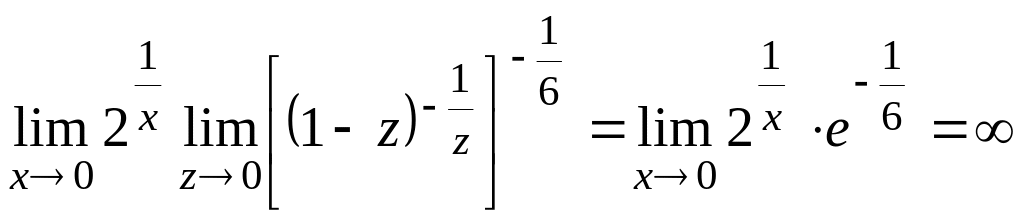