
Функции / Предел и непрерывность / Вычисление пределов №4
.docВычисление пределов.
При разложении многочлена на множители применяются формулы:
![]()
![]()
![]() ,
где
,
где
![]() и
и
![]() -
корни квадратного трехчлена.
-
корни квадратного трехчлена.
Найти пределы функций, не пользуясь правилом Лопиталя.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
|
Решение:
а)
Имеем неопределенность
вида
![]() .
Для ее раскрытия разложим квадратные
трехчлены на линейные множители по
формуле
.
Для ее раскрытия разложим квадратные
трехчлены на линейные множители по
формуле
![]()
Имеем:

Сократив общий
множитель
![]() ,
получим:
,
получим:
![]()
б)
Имеем неопределенность
вида
.
Для ее раскрытия умножим, и числитель,
и знаменатель данной дроби на выражение,
сопряженное числителю (знаменателю), а
именно:
![]() .
Имеем:
.
Имеем:
![]()
Для упрощения числителя воспользуемся формулой:
|
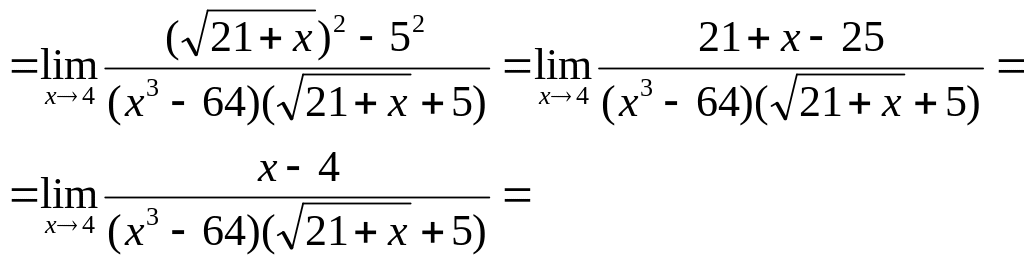
-
Разложим первый сомножитель знаменателя по формуле:
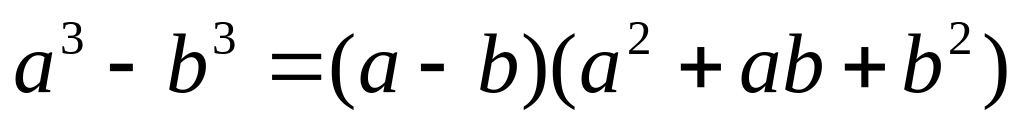 ,
где
,
где


в)
Если числитель и
знаменатель дроби представляют собой
алгебраические многочлены и имеется
неопределенность вида
![]() ,
то для ее раскрытия и числитель, и
знаменатель делят на х в старшей степени.
В данном случае старшая степень 3,
поэтому, и числитель, и знаменатель
делим на
,
то для ее раскрытия и числитель, и
знаменатель делят на х в старшей степени.
В данном случае старшая степень 3,
поэтому, и числитель, и знаменатель
делим на
![]() ,
имеем:
,
имеем:
![]()

(по теореме о пределе частного, имеем)

(по теореме о пределе суммы, имеем)

г)
Имеем также неопределенность вида .
Старшая степень
х равна 5. Поэтому делим и числитель, и
знаменатель на
![]() .
Имеем:
.
Имеем:

т.к. предел числителя равен 2, а знаменателя 0.
д)
Для вычисления данного предела, и числитель, и знаменатель дроби делим на , имеем:

е)
Имеем неопределенность
вида:
![]() .
.
Для ее раскрытия воспользуемся вторым замечательным пределом:
![]() или
или
![]()
![]()

ж)
Имеем неопределенность
вида
.
Для ее раскрытия будем использовать
первый замечательный предел:
![]()
Для этого сделаем следующие преобразования:
![]()



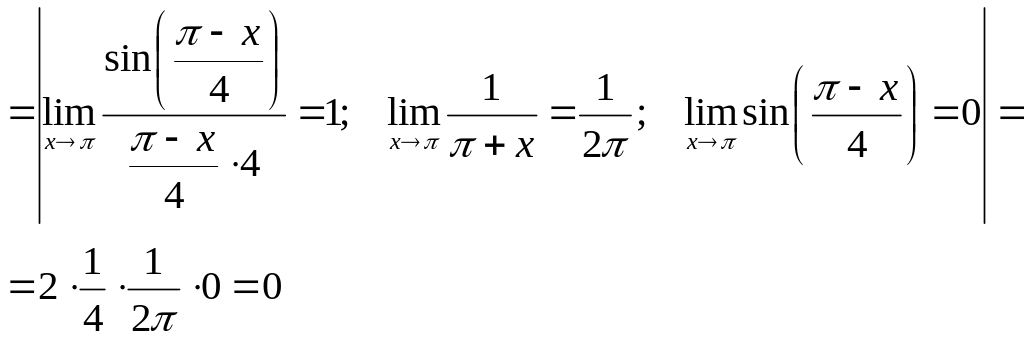
Пример
Найти
предел ![]()
Решение.
Подставляем
значение:
![]()
Пришли к степенной неопределенности.
Преобразуем
исходный предел:

Таким
образом, решение сводится к пределу 

В преобразованиях была использована замена логарифма на эквивалентную бесконечно малую функцию.
Таким
образом, исходный предел равен ![]()
Этот же предел можно было вычислить с использованием второго замечательного предела:


Таким образом, решение свелось к пределу

Далее решите самостоятельно!.

