Вектора / Решение задач

Векторы   лежат в одной плоскости и образуют попарно друг с другом углы 2π/3. Разложить вектор   по векторам   и  ,

Если   .

Решение.

Найдем единичные векторы, направленные, как и векторы   и   

(см. рисунок):   или  .

Тогда    и  .

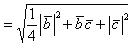
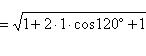
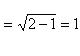Следовательно, вектор   - единичный.

Так как   , то угол между векторами   и   равен 180°,

т. е. эти векторы противоположно направлены;

поэтому   .

Задача 15.

Найти равнодействующую двух сил   и  , модули которых равны

 F₁ = 5, F₂ = 7, угол между ними θ = 60^°. Определить также углы α и β, образуемые равнодействующей с силами   и  .

Решение.

По формуле

(теорема косинусов для треугольника)

находим

Или

Углы   и   находим из треугольника ABC, пользуясь теоремой синусов

( ):

Но

и тогда

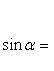
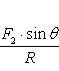
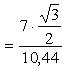
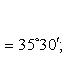
Контроль: ( ).

Задача 16.

На точку действуют три силы  ,   и  , проекции которых на оси прямоугольной системы координат таковы:

X	2	4	-5
Y	1	-3	4
Z	5	1	2

Найти величину и направление равнодействующей.

Решение.

Равнодействующая   . Обозначим проекции равнодействующей через X, Y, Z, а проекции сил  ,  ,   - соответственно через X₁, Y₁, Z₁, X₂, Y₂, Z₂ и X₃, Y₃, Z₃.

По формулам:  проекция суммы векторов на какую-нибудь ось равна алгебраической сумме проекций этих векторов на ту же ось

a_x = a_1x + a_2x + a_3x + ... + a_nx;           a_y = a_1y + a_2y + a_3y + ... + a_ny;      a_z = a_1z + a_2z + a_3z + ... + a_nz.          

Имеем

X = X₁ + X₂ + X₃;  X = 1, Y = Y₁ + Y₂ + Y₃;  Y = 2, Z = Z₁ + Z₂ + Z₃;  Z = 8.

По формуле длины вектора

величина равнодействующая R будет равна корню квадратному из суммы квадратов проекций   на координатные оси:

По формулам

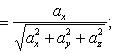
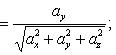
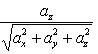
находим направляющие косинусы равнодействующей

Задача 17.

Дана сила   и точка ее приложения A(2, -1, 3). Найти момент силы относительно начала координат и углы, составляемые им с координатными осями.

Решение.

Момент силы относительно начала координат равен векторному произведению радиуса-вектора точки A приложения силы на силу  ,

т. е.  .

Если вектор имеет начало в начале координат,

а его конец A имеет координаты x, y и z, то тогда его проекции на координатные оси равны координатам его конца:

a_x = x; a_y = y; a_z = z.

В этом случае вектор называется радиусом-вектором точки A.

Радиус-вектор точки обозначается обыкновенно через (см. рисунок):

     

а модуль радиуса-вектора точки A(x, y, z) вычисляется по формуле

     

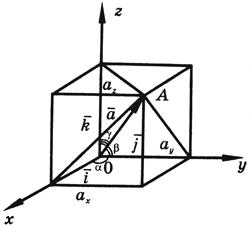
Проекция радиуса-вектора точки A на координатные оси равны координатам точки A :

r_x = x = 2;  r_y = y = -1;  r_z = z = 3;

Проекции X, Y, Z силы   на координатные оси нам также известны из условия задачи:

X = 3;  Y = 4;  Z = -2,

Выражение векторного произведения через проекции векторов и на координатные оси прямоугольной системы координат дается формулой

     

и тогда для нашего случая 

Отсюда

m_x = -10;  m_y = 13;  m_z = 11;

и модуль момента

Направляющие косинусы вектора   равны

а углы, составляемые моментом силы с координатными осями, следующие:

Контроль: должно быть  .

У нас  .