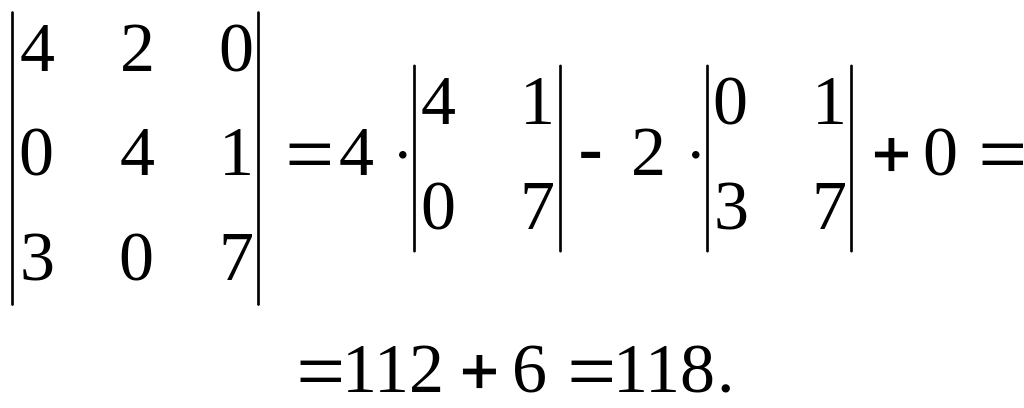Вектора / Решение задач

Решение задач

Задача 1.

При каких значениях α и β  вектор   перпендикулярен вектору  , если  ?

Решение.

Так как  , то  =3;

откуда β = ±2.

Векторы   и   перпендикулярны, тогда, когда  ,

т. е. 3·2 + (-1)·β + α·1 = 0; откуда α = β - 6.

При β = 2, имеем α = 2 - 6 = -4;

при β = -2, имеем α = -2 - 6 = -8.

Задача 2.

Два вектора   и   определены своими проекциями  {7, 2, -1} и

  {1, 2, -3}. Найти скалярное произведение этих векторов и угол между ними.

Решение.

По формуле

подставляя сюда проекции данных векторов, получим

по формуле

откуда

Таким образом, для определения   нам осталось определить модули векторов   и  .

По  формуле длины вектора (модуль вектора)

Отсюда

получаем, что

Задача 3.

Определить угол между векторами   и  , заданными своими проекциями  {2, 1, -2},  {1, -4, 2}.

Решение.

По формуле угла между векторами

     

Все величины, стоящие в числителе этой дроби, известны из условия задачи. Неизвестными являются модули векторов   и 

Подставляя в      числа, получим  ;

Задача 4.

Найти площадь параллелограмма, построенного на векторах 

.

Решение.

По определению векторного произведения двух векторов модуль векторного произведения равен площади параллелограмма, построенного на этих векторах. Поэтому для решения задачи найдем сначала векторное произведение   , а потом его модуль.

Векторное произведение   равно

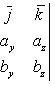
имеем

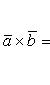
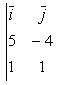
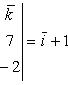
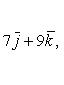
а модуль (длина) этого вектора

Искомая площадь параллелограмма

S = 19,26 кв. ед.

Замечание.

Векторное произведение   можно было определить по формуле

в которой следует взять

a_x = 5;  a_y = -4;  a_z = 7;

b_x = 1;  b_y = 1;  b_z = -2.

Задача 5.

Векторы    и    определены координатами своих концов: 

A(2, 4, 5);  B(-1, -3, -2);  C(4, 1, 7);  D(-2, 3, 10).

Найти: 1) векторное произведение  ;

2) его модуль;

3) направляющие косинусы векторного произведения.

Решение.

1) Найдем прежде всего проекции векторов   и   на координатные оси по формулам

a_x = x₂ - x₁;  a_y = y₂ - y₁;  a_z = z₂ - z₁,

Итак,   .

Тогда по формуле 

2) Модуль этого векторного произведения по его известным проекциям найдем:

3) Направляющие косинусы векторного произведения найдем по формулам (13).

Углы, образуемые вектором с координатными осями Ox, Oy и Oz, определяются из формул

           

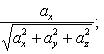
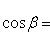
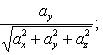      (13)

           

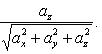
Задача 6.

Даны два вектора:   и  .

Найти проекции на координатные оси суммы и разности этих векторов.

Решение.

Составим сумму и разность этих векторов:

Ответ:  ;

Задача 7.

Вектор   задан координатами своих концов A и B: 

A(2, 1, -4); B(1, 3, 2). Найти проекции вектора   на координатные оси и его направляющие косинусы.

Решение.

Проекции вектора   на координатные оси находим по формулам

a_x = x₂ - x₁; a_y = y₂ - y₁; a_z = z₂ - z₁,

a_x = -1; a_y = 2; a_z = 6;

Направляющие косинусы определяем по формулам

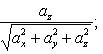
Задача 8.

Найти площадь треугольника, координаты вершин которого известны: A(-2, 1, 2); B(3, -3, 4); C(1, 0, 9).

Решение.

Рассмотрим векторы   и  . Площадь треугольника ABC есть половина площади параллелограмма, построенного на векторах   и  . Площадь параллелограмма, построенного на векторах   и  , есть модуль векторного произведения  , а потому площадь треугольника ABC есть

Надо найти векторное произведение  , а потом половину его модуля.

Проекции векторов   и   на координатные оси найдем по формулам. 

Если для вектора известны координаты его начала A(x₁, y₁, z₁) и координаты его конца B(x₂, y₂, z₂), то проекции вектора на координатные оси определяются по формулам

a_x = x₂ - x₁; a_y = y₂ - y₁; a_z = z₂ - z₁,     

По формуле (27)   

для векторного произведения векторов найдем, что

Модуль вектора   найдем по формуле (4):

S_ABC = 19,787 кв. ед.

Задача 9.

Дан треугольник с вершинами А(-1;1;2); В(0;2;3); С(1;1;0). Вычислить площадь треугольника.

Решение: Вычислим площадь параллелограмма, используя формулу: , где - векторы, на которых построен параллелограмм. В качестве векторов и используем и .

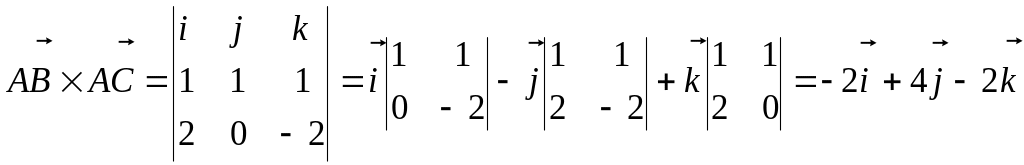
Задача 10.

Найти векторное произведение векторов , .

Решение:

Составляем матрицу:

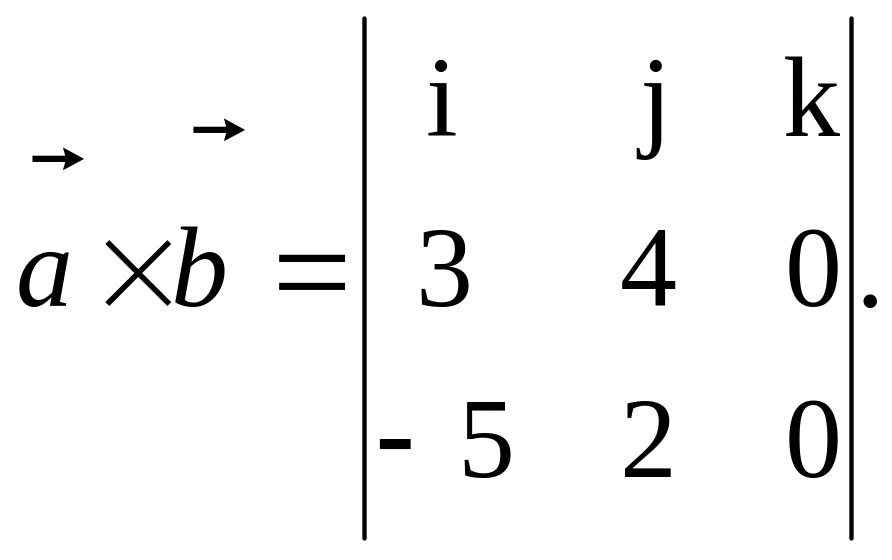
Находим координату х_с; у_с; z_c векторного произведения :

.

Записываем координаты вектора :

.

Задача 11.

Найти площадь треугольника с вершинами в точках А(1, 3, 0); В(2, 5, 0); D(-4, 3, -2).

Решение. Воспользуемся определением векторного произведения.

Введем вектора:

Длина вектора равна площади параллелограмма построенного на векторах Площадь треугольника S_ABD равна половине площади параллелограмма, поэтому:

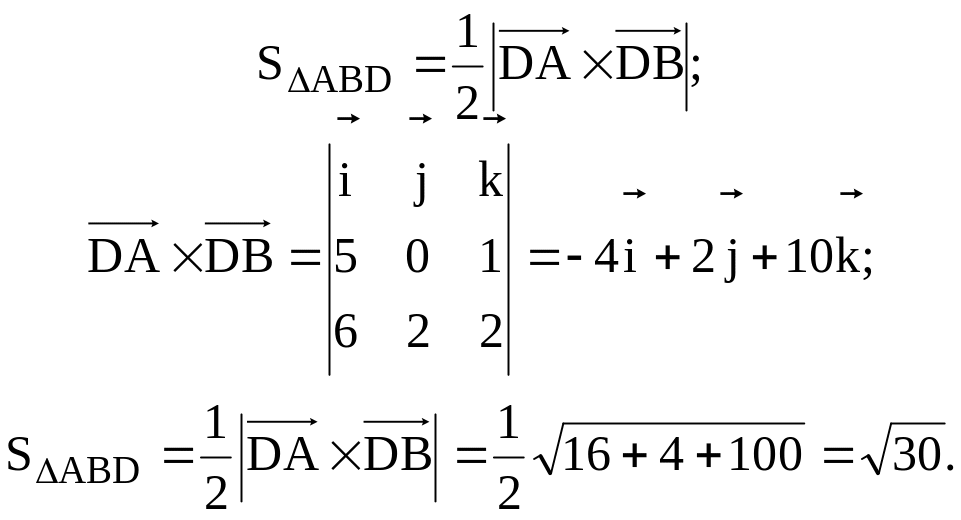
Задача 12.

Вычислить объем параллелепипеда построенного на векторах ; ; .

Решение. Вычислим смешанное произведение векторов . Для этого запишем и вычислим определитель третьего порядка

y z x	Вычисленное значение определителя в соответствии с графическим представлением смешанного произведения векторов будет равно объему параллелепипеда, построенного на векторах (рис. 1)
Рис. 1

Задача 13.

Даны координаты вершин пирамиды A₁(5, 1, -4), A₂(1, 2, -1), A₃(3, 3, -4) и A₄(2, 2, 2). Определить ее объем.

Решение.

Рассмотрим три вектора:  ,   и  . Поступая так же, как и при решении задачи, по формуле (32) нам надо знать проекции векторов на оси прямоугольной системы координат. Записывая проекции вектора рядом с его названием, получаем  ; и тогда

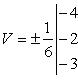
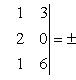
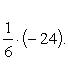
V = 4 куб. ед.

В правой части выбран знак минус, так как определитель равен -24 (отрицателен).

Задача 14.