Вектора / Векторы

     (25)

или

     (26)

Основные свойства векторного произведения:

1) Векторное произведение равно нулю, если векторы и коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):

Векторное произведение не обладает свойством переместительности.

3) (распределительное свойство).

Выражение векторного произведения через проекции векторов и на координатные оси прямоугольной системы координат дается формулой

     (27)

Векторное произведение можно записать с помощью определителя

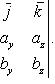      (28)

Проекции векторного произведения на оси прямоугольной системы координат вычисляются по формулам

     (29)

и тогда на основании (4)

     (30)

Механический смысл векторного произведения состоит в следующем: если вектор - сила, а вектор есть радиус-вектор точки приложения силы, имеющий свое начало в точке O, то момент силы относительно точки O есть вектор, равный векторному произведению радиуса-вектора точки приложения силы на силу , т. е.

19. Векторно-скалярное произведение трех векторов , и или смешанное их произведение вычисляется по формуле

      (31)

Абсолютная величина векторно-скалярного произведения (смешанного произведения) равна объему параллелепипеда, построенного на векторах , и .

Объем пирамиды, построенной на векторах , и , получим по формуле

     (32)

причем знак перед определителем должен быть выбран так, чтобы объем V был положительным (предполагается, что векторы , и не лежат в одной плоскости).

20. Три вектора , и называются компланарными, если они лежат в одной плоскости или параллельны одной и той же плоскости.

Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.

 = 0   

21. Фиксированная тройка некомпланарных векторов с общим началом в фиксированной точке О называется афинной системой координат или базисом (на плоскости два неколлинеарных вектора). Координаты вектора – это проекции вектора на векторы базиса.

В случае декартовой прямоугольной системы базисные векторы принято обозначать буквами . Каждый из векторов имеет длину, равную единице, причем эти три вектора взаимно ортогональны и образуют правую тройку.

22. Пусть

Длина вектора (33)

23. Пусть

Угол φ между векторами и определяется по формуле:

(34)

24. Скалярное произведение

Найдем скалярные произведения тройки базисных векторов:

Скалярное произведение векторов в координатной форме равно сумме произведений их соответствующих координат

(35)

Необходимым и достаточным условием ортогональности двух векторов и является равенство

(36)

25. Векторное произведение обозначают

Модуль векторного произведения равно площади параллелограмма, построенного на приведенных к общему началу векторах и

Векторное произведение векторов в координатной форме

. (37)

Если векторы коллинеарны, то координаты их пропорциональны, т.е.

(38)

26. Смешанное произведение равно объему параллелепипеда, построенного на приведенных к общему началу векторах , и , взятому со знаком плюс, если тройка векторов правая, и со знаком минус, если тройка левая.

Поэтому = V параллелепипеда.

Если три вектора , и определены своими декартовыми прямоугольными координатами то смешанное произведение этих векторов равно определителю, строки которого соответственно равны координатам перемноженных векторов, т.е.:

27. Необходимым и достаточным условием компланарности трех векторов является рвенство нулю определителя, строками которого служат координаты этих векторов:

28. Основные задачи, связанные с векторным и смешанным произведением векторов.

1. Определение площади треугольника АВС

2. Определение объема тетроэдра:

3. Определение высоты тетроэдра: