Вектора / 6. Векторный базис на плоскости и в пространстве

Векторный базис на плоскости и в пространстве.

45. Любые два неколлинеарных вектора попарно образуют векторный базис на плоскости.

Два вектора на плоскости ( а₁; а₂) и (b₁; b₂) коллинеарны, если координаты этих векторов пропорциональны:

=

46. Любые три некомпланарных вектора образуют векторный базис в пространстве.

Необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя, строками которого служат координаты этих векторов (смешанное произведение векторов ):

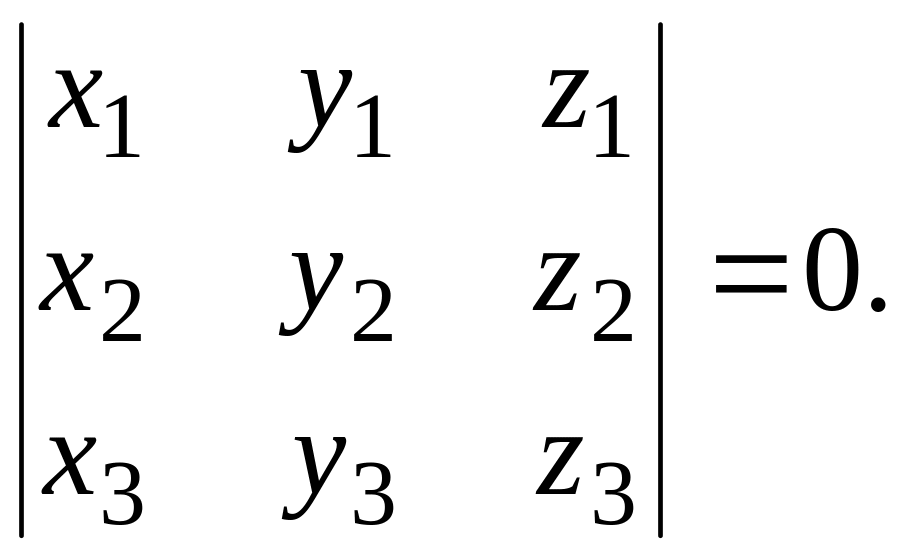
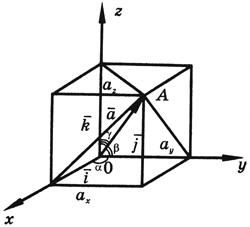
47. Фиксированная тройка некомпланарных векторов с общим началом в фиксированной точке О называется афинной системой координат или базисом в пространстве.

В случае декартовой прямоугольной системы в пространстве базисные векторы принято обозначать буквами . Каждый из векторов имеет длину, равную единице, причем эти три вектора взаимно ортогональны и образуют правую тройку. Направление векторов совпадает соответственно с направлением осей координат.

- векторы, по модулю равны единице и направлены по координатным осям Ox, Oy и Oz.

Разложение вектора с координатами ( а₁; а₂; а₃)

по трем координатным осям выражается формулой

48. Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю.

49. Скалярное произведение тройки базисных векторов:

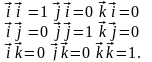
49. Если какой-либо вектор можно представить в виде линейной комбинации других векторов, то говорят о линейной зависимости данного вектора от элементов комбинации.

50. Определение. Если векторы образуют базис линейного пространства L, и вектор из L линейно выражается через векторы в виде , то числа называются координатами вектора x в базисе .

51.Определение. Векторы , … векторного пространства R называются линейно зависимыми, если существуют такие действительные числа λ₁; λ₂; … λ_n не равные одновременно нулю, при которых выполняется равенство:

Если равенство не выполняется, данные вектора , … являются линейно независимыми.