Вектора / 5. Смешаное произведение векторов

Часть 5

38. Векторно-скалярное произведение трех векторов , и или смешаное их произведение , где заданы координаты этих векторов (а_х; а_у; а_z) , (b_x; b_y; b_z) и (c_x; c_y; c_z), вычисляется по формуле:

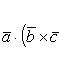
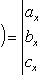
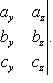
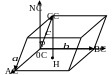
39. Абсолютная величина векторно-скалярного произведения (смешаного произведения) равна объему параллелепипеда, построенного на приведенных к общему началу векторах , и .

Результат вычисления определителя надо взять со знаком плюс, (тройка векторов правая), и со знаком минус (тройка левая), объем параллелепипеда величина положительная.

40. Объем пирамиды, построенной на векторах , и , получим по формуле

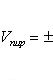
причем знак перед определителем должен быть выбран так, чтобы объем V был положительным (предполагается, что векторы , и не лежат в одной плоскости).

41. Три вектора , и называются компланарными, если они лежат в одной плоскости или параллельны одной и той же плоскости.

42. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.

= 0

43. Основные задачи, связанные с векторным и смешанным произведением векторов.

1. Определение площади треугольника АВС

2. Определение объема тетраэдра:

3. Определение высоты тетраэдра:

44. Свойства смешанного произведения векторов.

1. Свойства круговой переместительности

2. .

3. .

4. .

Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.