
Вектора / 4. Векторная алгебра Векторное произведение
..doc
![]()
![]()
![]()
![]()
Векторная алгебра. Часть 4Векторное произведение векторов.
33.
Векторным
произведением
векторов
![]() и
и
![]() называется
вектор
называется
вектор
![]() ,
который определяется следующими
условиями:
,
который определяется следующими
условиями:
1) Его модуль ( длина вектора) равен =
где
![]() -
угол между векторами
и
.
-
угол между векторами
и
.
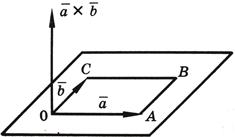
2) Вектор перпендикулярен к плоскости, определяемой перемножаемыми векторами и
3) Вектор направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы и , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки — система векторов в этом случае называется правой тройкой векторов.(см. рисунок).
Векторное произведение векторов и обозначается символом
![]() ;
;
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]() - площадь
параллелограмма, построенного на
векторах
и
численно равна модулю векторного
произведения
- площадь
параллелограмма, построенного на
векторах
и
численно равна модулю векторного
произведения
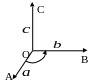
Правая
система векторов
![]() ,
,![]() ,
,
![]() .
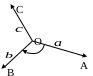
Левая
система векторов
,
,
.
.
Левая
система векторов
,
,
.
34. Основные свойства векторного произведения:
Свойства.
1.
![]()
2.
![]() .
.
3.
![]() .
.
4.
![]()
5. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
Достаточность:
Пусть вектора
![]() и
и
![]() коллинеарны. Тогда угол между ними φ=
00
и, следовательно, sinφ
= 0 и, в силу определения, векторное
произведение равно 0.
коллинеарны. Тогда угол между ними φ=
00
и, следовательно, sinφ
= 0 и, в силу определения, векторное
произведение равно 0.
Необходимость:
Так
как
и
ненулевые векторы, то
![]() тогда равенство
тогда равенство
![]() и из определения векторного произведения
следует, что sinφ
= 0, т.е. вектора
и
коллинеарны.
и из определения векторного произведения
следует, что sinφ
= 0, т.е. вектора
и
коллинеарны.
35. Выражение векторного произведения через проекции векторов (аx; аy; аz) и (bx; by; bz) на координатные оси прямоугольной системы координат задается формулой
![]()
![]()
![]()
![]()
![]()
![]()
Векторное произведение можно записать с помощью определителя
![]()
![]()
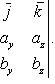
Для вычисления площади параллелограмма, построенного на векторах, надо вычислить векторное произведение и найти модуль векторного произведения. В этом заключается геометрический смысл векторного произведения.
36. Проекции векторного произведения на оси прямоугольной системы координат вычисляются по формулам
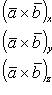
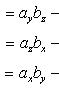
![]()
Длина вектора (модуль векторного произведения):
![]()
![]()
![]()
37.
Механический
смысл векторного произведения
состоит в следующем: если вектор
![]() -
сила, а вектор
-
сила, а вектор
![]() есть
радиус-вектор точки приложения силы,
имеющий свое начало в точке O,
то момент силы
относительно
точки O
есть
радиус-вектор точки приложения силы,
имеющий свое начало в точке O,
то момент силы
относительно
точки O
![]()
![]() есть
вектор, равный векторному произведению
радиуса-вектора
точки
приложения силы на силу
,
т. е.
есть
вектор, равный векторному произведению
радиуса-вектора
точки
приложения силы на силу
,
т. е.
![]()
![]()
![]()
Задача 1. Найти площадь параллелограмма, построенного на векторах
![]()
![]()
![]()
![]() .
.
Решение.
По
определению векторного произведения
двух векторов модуль векторного
произведения равен площади параллелограмма,
построенного на этих векторах. Поэтому
для решения задачи найдем сначала
векторное произведение
![]() по
формуле
по
формуле
![]()
![]()
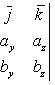
имеем:
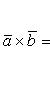
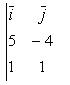
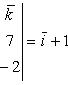
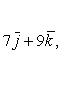
Определитель студенту вычислить самостоятельно.
Вычислим теперь модуль векторного произведения по формуле длины вектора.
Модуль
(длина)
этого вектора
![]()
![]()
![]()
![]()
![]() Искомая
площадь параллелограмма S=
19,26 кв. ед.
Искомая
площадь параллелограмма S=
19,26 кв. ед.
