
Вектора / 3. Векторная алгебра Скалярное произведение векторов
.docВекторная алгебра Часть 3
Скалярное произведение векторов.
24.
Скалярным
произведением
двух векторов
![]() и
и
![]() называется
число,
равное произведению модулей этих
векторов на косинус угла между ними.
называется
число,
равное произведению модулей этих
векторов на косинус угла между ними.
Скалярное
произведение векторов
и
обозначается
символом![]() .
Если обозначить угол
между векторами
и
через
.
Если обозначить угол
между векторами
и
через
![]() ,
для скалярного произведения будем иметь
,
для скалярного произведения будем иметь
![]() =
=![]()
![]()
![]()
25.
Пусть
даны векторы
и
в
пространстве с
координатами
![]()
Скалярное произведение векторов в пространстве и в координатной форме равно сумме произведений их соответствующих координат
![]()
26.
Угол
φ между векторами
![]() и
и
![]() определяется по формуле:
определяется по формуле:
![]()
В знаменателе дроби стоит произведение длин векторов и , а в числителе дроби - скалярное произведение этих векторов.
27. Скалярное произведение векторов на плоскости
(х1; у1) и (х2; у2) в координатной форме равно сумме произведений их соответствующих координат
![]()
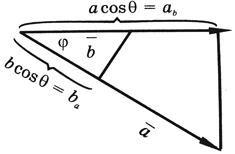
28. Из формулы = можно выразить скалярное произведение двух векторов и иначе - это произведение модуля одного из них на проекцию второго на направление первого вектора (см. рисунок):
![]()
![]()
![]()
откуда
![]()
![]()
![]()
![]() .
.
29.
Скалярное произведение двух перпендикулярных
векторов равно нулю,
так как в этом случае
![]()
![]()
![]() .
.
30. Скалярное произведение имеет свойства, аналогичные свойствам произведений чисел:
Свойства:
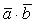
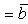
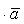 (переместительное
свойство);
(переместительное
свойство);(α ) = α( ) (сочетательное свойство относительно числового множителя α);
( + )
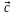 =
+
(распределительное свойство относительно
суммы векторов);
=
+
(распределительное свойство относительно
суммы векторов);> 0, если - ненулевой вектор, и = 0, если - нулевой вектор.
Скалярный квадрат вектора
 .
.Необходимым и достаточным условием ортогональности двух ненулевых векторов является равенство нулю их скалярного произведения.
Достаточность:
Пусть вектора и ортогональны, φ - угол между ними равен 90 градусов. Тогда cos φ = 0 и в силу определения скалярное произведение равно 0.
Необходимость:
Так
как
и
ненулевые вектора, то
![]() тогда из равенства
тогда из равенства
![]()
![]() =
0 и из определения
следует, что cos
φ
= 0, т. е. векторы
и
ортогональны, т.к. угол между векторами
должен в этом случае равняться 900.
=
0 и из определения
следует, что cos
φ
= 0, т. е. векторы
и
ортогональны, т.к. угол между векторами
должен в этом случае равняться 900.
31. Если векторы и заданы проекциями на координатные оси
![]()
![]()
![]()
![]()
![]()
![]() ,
то
их скалярное произведение вычисляется
по формуле
,
то
их скалярное произведение вычисляется
по формуле
![]()
![]()
![]()
а косинус угла между этими векторами определяется по формуле
![]()
![]()
Если векторы и перпендикулярны (ортогональны), то их скалярное произведение равно нулю, и тогда
axbx + ayby + azbz = 0
или
![]()
![]()
![]()
![]()
![]()
![]()
32.
Если углы, образуемые вектором
с
координатными осями, обозначить через
![]()
![]() ,
а углы, образуемые вектором
с
координатными осями, - через
,
а углы, образуемые вектором
с
координатными осями, - через
![]()
![]() ,
то
косинус
угла
между
векторами
и
определяется
по формуле
,
то
косинус
угла
между
векторами
и
определяется
по формуле
![]()
![]()
![]()
![]()
![]()
![]()
![]() Задача
1.
Даны
два вектора
Задача
1.
Даны
два вектора
![]()
![]() и
и
![]()
![]() . Найти
скалярное произведение этих векторов.
. Найти
скалярное произведение этих векторов.
Решение: (2; 3; -4) и
![]() (-3; 2; 5),
=
2*(-3) + 3* 2 — 4*5= -20
(-3; 2; 5),
=
2*(-3) + 3* 2 — 4*5= -20
Задача
2.
При каких значениях α
и
β
вектор
![]() перпендикулярен вектору
перпендикулярен вектору
![]() ,
если
,
если
![]() ?
?
Решение.
Так
как
,
то по формуле длины (модуля) вектора
![]() =3;
=3;
( ) 2 = 3 2, Находим β 2 =9 -4 -1 откуда β = ±2.
Векторы
![]() и
перпендикулярны, тогда, когда
и
перпендикулярны, тогда, когда
![]() ,
,
при и произведение должно быть равным нулю
3·2 + (-1)·β +α·1 = 0; откуда α= β - 6.
1) при β = 2, имеем α = 2 - 6 = -4;
2) при β = -2, имеем α = -2 - 6 = -8.
Ответ: 1) (3; -1; -4) и (2; 2; 1) взаимно перпендикулярны.
Проверка: = 3*2 -1*2 -4*1 =0
![]()
![]() 2) (3;
-1; -8) и (2; -2; 1) взаимно перпендикулярны.
2) (3;
-1; -8) и (2; -2; 1) взаимно перпендикулярны.
Проверка 3*2- 1*(-2) - 8*1 =0
![]() Задача
3.
Коммерческий
банк, участвующий в строительстве
Задача
3.
Коммерческий
банк, участвующий в строительстве
многоэтажных автомобильных стоянок в Калининграде, предпринял
усилия для получения кредитов в трех коммерческий банках: «ВТБ»,
«Альфа-банк», «Сбербанк». Каждый из них предоставил кредиты
в размерах соответственно 20, 30 и 40 млрд. руб. под годовую ставку
40, 25 и 30 %.
Решение. В данном примере речь идет о двух векторах:
трехмерном векторе кредитов (20; 30; 40)
и векторе процентных
ставок
![]() (40;
25; 30).
(40;
25; 30).
Используя простой расчет, управляющий коммерческим банком
может определить, сколько придется платить по истечении года на
кредиты, взятые у трех банков, применяя скалярное произведение.
В конце года банку ВТБ придется вернуть 20 млрд. руб и еще и 40% от этой суммы (20 + 20* 0,4 =20(1 + 0,4) = 20 *1,4= 28).
Аналогично и другим банкам.
Вектор заменяем на вектор (1,40; 1, 25; 1,30).
Выплатить по кредиту надо:
=20 *1, 40 + 30 *1,25 + 40 *1,30 = 28 +37,5 + 52 =117, 5 млрд. р
