Вектора / 2. Векторная алгебра Проекции

Векторная алгебра. Часть 2.

9. Расстояние между точками A(x₁, y₁, z₁) и B(x₂, y₂, z₂) в пространстве =

Если вектор задан координатами точек А(х_а ; у_а) и В(х_в ; у_в ) на плоскости, то длина вектора (модуль вектора) определяется по формуле = =

Для вектора в пространстве, если известны координаты его начала A(x₁, y₁, z₁) и координаты его конца B(x₂, y₂, z₂), модуль вектора (длина вектора) определится по формуле

= =

10. Единичным вектором, или ортом данного вектора, называется вектор, совпадающий по направлению с данным вектором и имеющий модуль (длину), равный единице.

11. Проекцией вектора на ось называется длина отрезка A'B', заключенного между проекциями конца и начала вектора на эту ось. Этой длине приписывается знак плюс, если направление отрезка A'B' совпадает с направлением оси, и знак минус, если его направление противоположно направлению оси.

Проекция вектора на ось есть скалярная величина, равная произведению модуля проецируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).

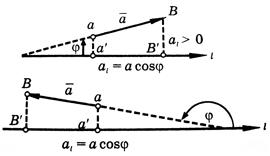
Проекция вектора на ось обозначается через a_l или , а угол между осью и вектором будем обозначать ,

=

12. Проекция вектора на вектор находится по формуле

Проекция вектора на вектор находится по формуле

=

13. Если углы, образованные вектором (а _x; а_y; а_z) с координатными осями Ox, Оy и Oz, то для вектора в пространстве проекции вектора на координатные оси Ox, Oy и Oz прямоугольной системы координат будут равны:

14. Модуль вектора (длина вектора) через его проекции на оси прямоугольной системы координат вычисляется по формуле

=

Например, для вектора (2; 3; 4) = =

15. Если векторы (a_1x; a_1y ; a_1z) и ( a_2x; a_2y; a_2z) равны, то равны и их проекции: a_1x = a_2x; a_1y = a_2y; a_1z = a_2z.

16. Если для вектора в пространстве известны координаты его начала A(x₁, y₁, z₁) и координаты его конца B(x₂, y₂, z₂), то проекции вектора на координатные оси определяются по формулам

a_x = x₂ - x₁; a_y = y₂ - y₁; a_z = z₂ – z₁,

( x₂ – x₁; y₂ - y₁; z₂ – z_1).

17. Вектор равен нулю, если все три его проекции равны нулю (этим положением пользуются, например, в механике при выводе необходимых и достаточных условий равновесия тела под действием системы сил, проходящих через одну точку).

Задача 1. Векторы и определены координатами своих концов: A(2; 4; 5), B (-1; -3; -2), C(4; 1; 7) и D(-2; 3; 10). Найти:

1) длину вектора 2) проекции вектора на координатные оси:

1)

2) а_х =-2 -4 = -6; а_у= 3 -1 = 2; а_z=10 – 7 = 3 (-6 ; 2 ; 3)

18. Проекция суммы векторов на какую-нибудь ось равна алгебраической сумме проекций этих векторов на ту же ось. Из векторного равенства следуют такие три скалярные равенства:

a_x = a_1x + a_2x + a_3x + ... + a_nx; a_y = a_1y + a_2y + a_3y + ... + a_ny; a_z = a_1z + a_2z + a_3z + ... + a_nz.

19. Если - векторы, по модулю равные единице и направленные по координатным осям Ox, Oy и Oz, то разложение вектора по трем координатным осям выражается формулой

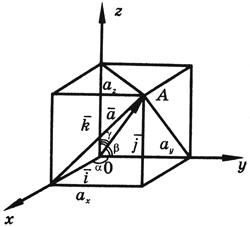
Где a_x, a_y и a_z - проекции вектора на координатные оси - называются координатами вектора.

Например, вектор из задачи 1. можно записать

(-6 ; 2 ; 3) = -6 +2 + 3

20. Если вектор имеет начало в начале координат, а его конец A(x; y; z) имеет координаты x, y и z, то тогда его проекции на координатные оси равны координатам его конца:

a_x = x; a_y = y; a_z = z.

В этом случае вектор называется радиусом-вектором точки A. Радиус-вектор точки обозначается обыкновенно через (см. Рисунок): , а модуль радиуса-вектора точки A(x; y; z) вычисляется по формуле длины вектора

21. Углы, образуемые вектором с координатными осями Ox, Oy и Oz, определяются из формул:

с осью Ох

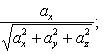
с осью Оу

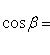
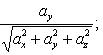
с осью Oz

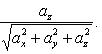
Косинусы, определяемые по этим формулам, называются направляющими косинусами вектора .

Для направляющих косинусов вектора имеет место формула

т. е. сумма квадратов косинусов углов, образуемых вектором с тремя взаимно перпендикулярными осями, равна единице.

22. Если , т. е. если - единичный вектор, обозначаемый обыкновенно , то его проекции на координатные оси вычисляются по формулам

т. е. проекции единичного вектора на оси прямоугольной системы координат Ox, Oy и Oz равны соответственно направляющим косинусам этого вектора.

Имеет место формула:

23. Если даны два вектора и

То сумма векторов, заданных координатами, равна