Основные сведения из векторной алгебры.

1. Вектор обозначается графически отрезком прямой, на котором ставится стрелка, указывающая направление вектора .

Вектор можно обозначать , где т. A - начало и т. B - конец вектора.

Можно обозначать вектор одной буквой с черточкой над ней, например, , а модуль этого вектора обозначается .

2. Вектор считается заданным, если известна его длина и направление.

Вектор можно задать координатами начала и конца А(х₁ ; у₁) и В(х₂ ; у₂ ). На рис. 1 приведен вектор , начальная точка которого имеет координаты А(2; 5) , а конечная точка В(6; 7).

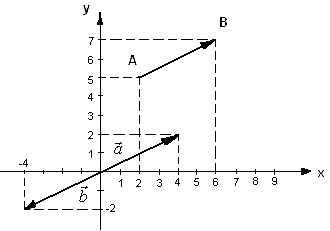
Рис. 1

Вектор можно задать координатами. Для задания координат вектора нужно из координат конечной точки вычесть координаты начальной точки: (х₂ -х₁; у₂ -у₁).

Для , начальная точка которого имеет координаты А(2; 5) , а конечная точка В(6; 7), (6 - 2; 7- 5), т. е. (4; 2)

На рис. 1 приведен вектор (4; 2) равный вектору , так как он без изменения длины и направления получен параллельным переносом начала вектора в начало координат.

3. Для задания вектора в трехмерном пространстве должны быть определены три его координаты (x; y; z)

На рис. 2 показан вектор в трехмерном пространстве с координатами (2; 3; 4).

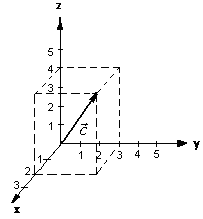
Рис. 2

4. Вектор равен нулю, если его модуль (длина) равен нулю. Такой вектор называется нулевым.

5. Два вектора и называются равными, если равны их модули, они лежат на параллельных прямых (коллинеарные) и направлены в одну и ту же сторону.

Два вектора с равными модулями, лежащие на параллельных прямых, но противоположно направленные, называются противоположными.

Вектор, противоположный вектору , обозначается через .

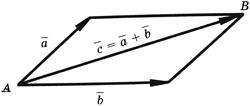
6. Сложение векторных величин, заданных графически, производится по одному из двух правил.

Правило параллелограмма: сумма двух векторов и , приведенных к общему началу, есть третий вектор , длина которого равна длине диагонали параллелограмма, построенного на векторах и , а направлен он от точки A( начала векторов , и ) к точке B.

Правило треугольников.

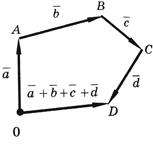
Сумму нескольких векторов, например , , и , строят так: берут произвольную точку O плоскости и из нее строят вектор , равный вектору ; из точки A проводят вектор , равный вектору , из точки B - вектор , равный вектору и, наконец, из точки C строят вектор , равный вектору .

Вектор , замыкающий полученную ломаную линию OABCD, и будет суммой векторов , , и (см. рисунок):

По такому же правилу строится и сумма любого числа векторов.

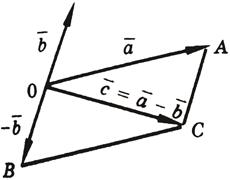
7. Разностью двух векторов и называется такой третий вектор , который равен сумме векторов и (см. рисунок). Вектор параллелен вектору , равен ему по модулю, но противоположно направлен:

8. При умножении вектора на скаляр k получается вектор , модуль которого равен модулю вектора , умноженному на k, т. е.

= k .

Направления векторов и совпадают, если k > 0, и они противоположны, если k < 0.

9. Два вектора, лежащие на параллельных прямых, независимо от того, направлены они одинаково или противоположно, называются коллинеарными.

Если два вектора в пространстве коллинеарны, то координаты их пропорциональны, т.е.

Если два вектора на плоскости (х₁ ; у₁) и (х₂ ; у₂ ), коллинеарны, то координаты их пропорциональны, т.е.

.