Матрицы / Обратная матрица

Обратная матрица

Матрица называется обратной квадратной матрице А, если при умножении этой матрицы на матрицу А как справа, так и слева получается единичная матрица:

Пример 1. Проверить является ли матрица обратной по отношению к матрице .

Вычислим произведение матриц:

.

Так как выполняется условие , то матрица В является обратной матрице АВ = Е.

Для существования обратной матрицы необходимо и достаточно чтобы ее определитель не равнялся нулю.

Если определитель матрицы равен нулю, то матрица называется вырожденной и для нее не существует обратной матрицы. Матрица, определитель которой не равен нулю |А| ≠ 0, называется невырожденной.

Алгоритм нахождения обратной матрицы.

1. Находим определитель исходной матрицы А. Если |А| = 0, то матрица является вырожденной и обратной матрицы не существует. Если |А| ≠ 0, то обратная матрица существует.

2. Находим алгебраические дополнения А_ij всех элементов матрицы А, составляем промежуточную матрицу из этих алгебраических дополнений и транспонируем промежуточную матрицу:

3. Составляем обратную матрицу по формуле:

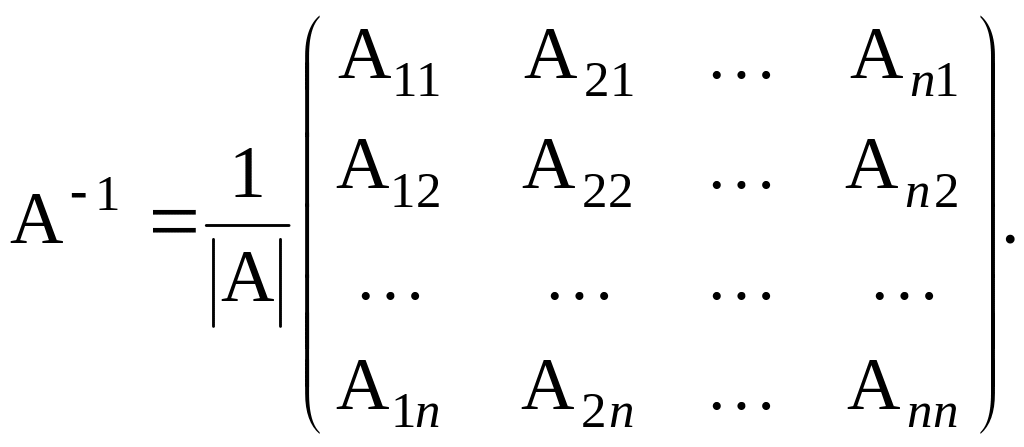
Пример2 .Найти матрицу обратную матрице А:

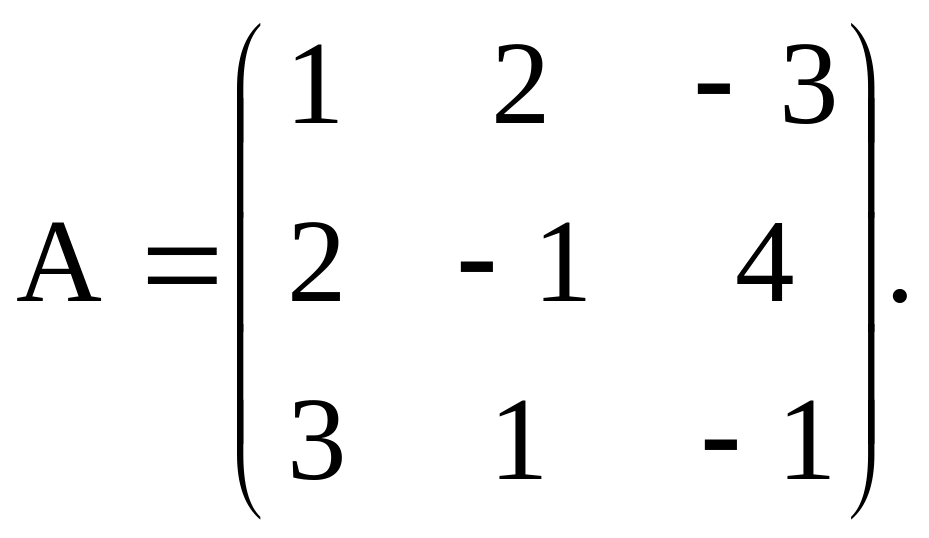
Решение.

1. Определитель матрицы А

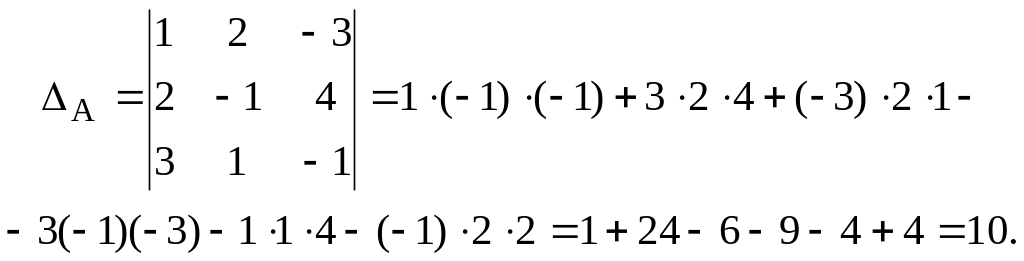
Матрица А невырожденная.

2.Находим алгебраические дополнения А_ij всех элементов матрицы А:

.

3.Составляем обратную матрицу по формуле

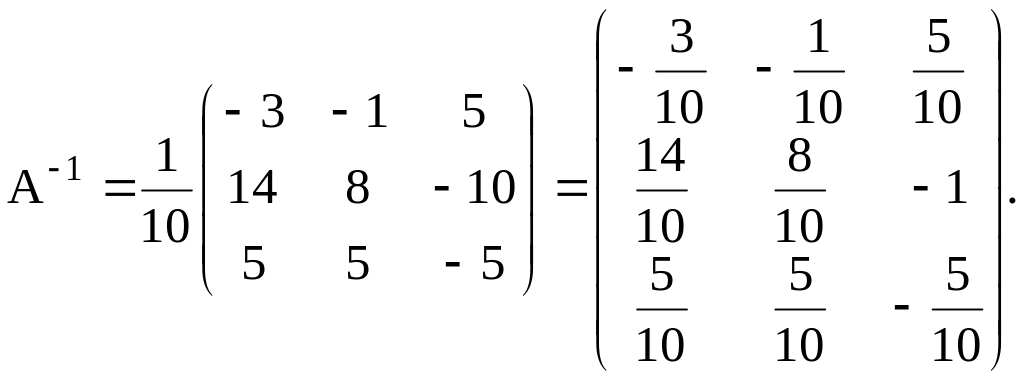
4. Проверяем правильность вычисления обратной матрицы по формуле :