Матрицы

Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Так же, волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.^[1]

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами.

Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество т строк и некоторое количество п столбцов.

Числа тип называются порядками матрицы.

В случае, если то m = п (количество строк матрицы равно количеству столбцов), матрица называется квадратной, а число

m = п — ее порядком.

В случае квадратной матрицы

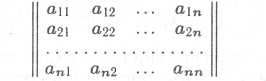
В для записи матрицы применяются либо сдво­енные черточки, либо круглые скобки:

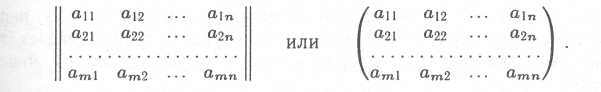
Для краткого обозначения матрицы будем использо­вать одну большую латинскую букву (например, А),

Числа, входящие в состав данной матрицы, называются ее элементами.

В записи aij первый индекс i означает номер строки,

а второй индекс j — номер столбца.

Основные операции над матрицами и их свойства.

Две матрицы считаются равными, если эти матрицы имеют одинаковые порядки и все их соответствующие элементы совпа­дают.

а) Сложение матриц.

Суммой двух матриц А и В называется матрица С =cij тех же порядков m и п, элементы которой равны

Ci =aij + bij (i = 1, 2,..., m ; j = 1, 2,..., n).

б) Умножение матрицы на число.

Произведением мат­рицы А на действительное число К (умножением матрицы на это число К) называется матрица С, каждый элемент которой равен произведению соответствующего элемента матриц А на это число К.

Для обозначения произведения матрицы на число используется запись С = К А

Разность С двух матриц А и В одних и тех же порядков m и п может быть получена по правилу С = А + (-1)B.

в) Перемножение матриц.

Матрицу А можно умножить не на всякую матрицу В.

Для умножения матрицы А на матрицу В необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В.

Правило: элемент Cij, стоящий на пересечении i-й строки и j-го столбца матрицы С = АВ, равен сумме попарных произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.

Произведение двух матриц не подчиняется переместительному закону. АВВА.

Умножение матриц

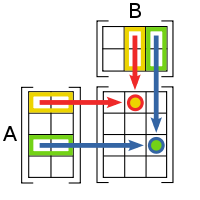
Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Задание 1. Найти произведение матриц А и В,

А= ; В= ,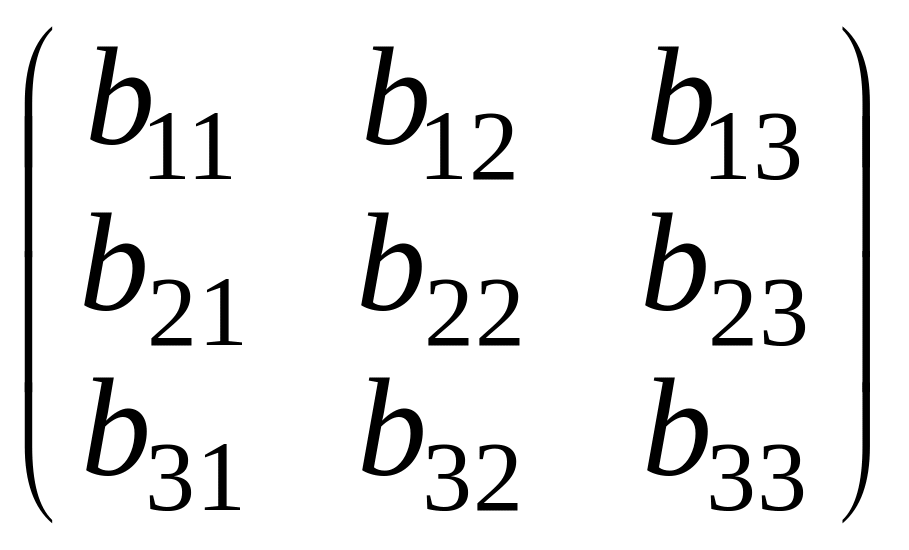

если , .

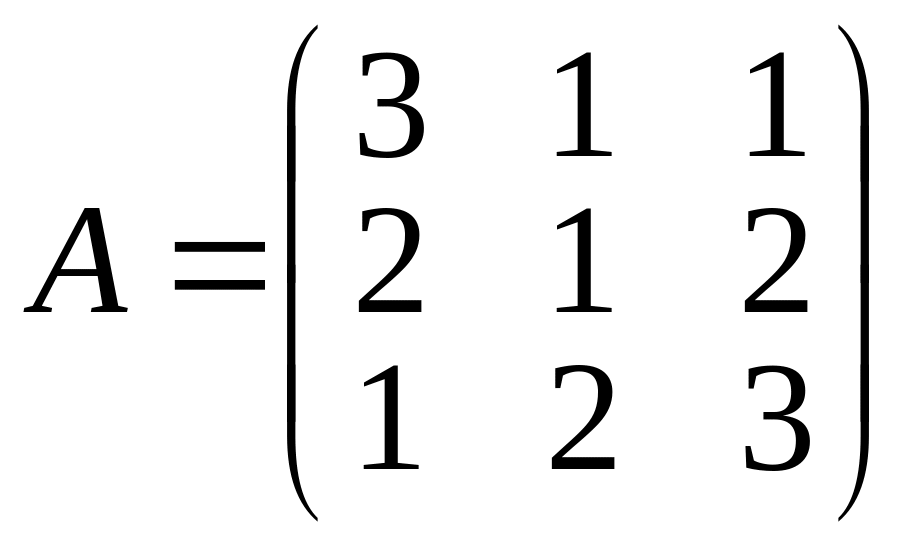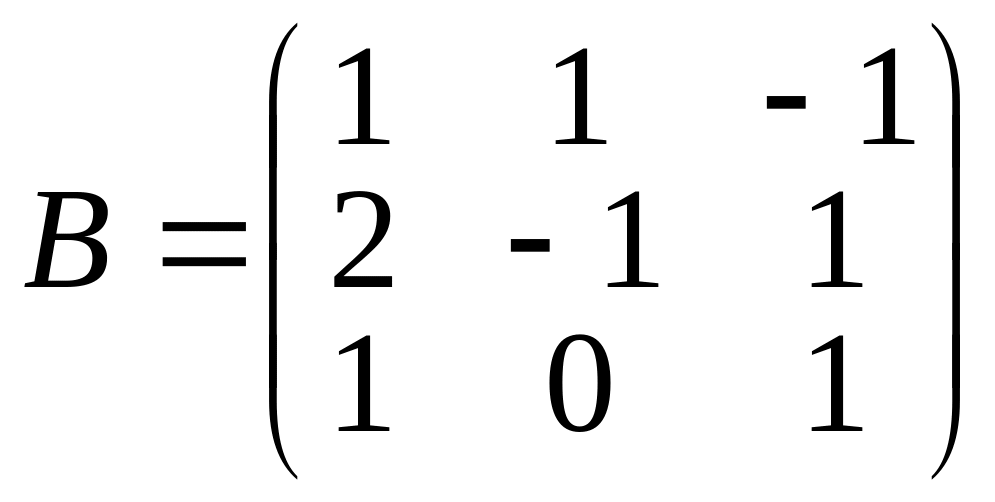Решение. Найдем каждый элемент матрицы-произведения:

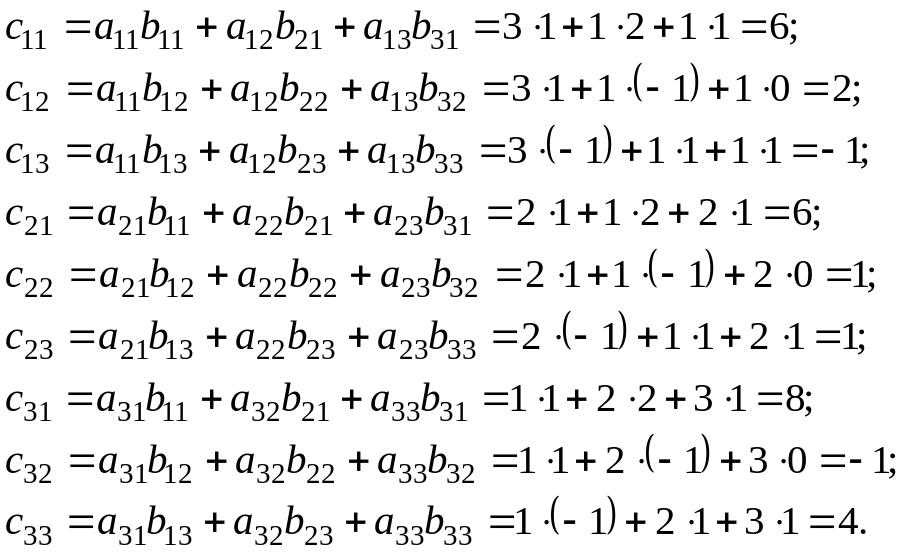
Следовательно,

.

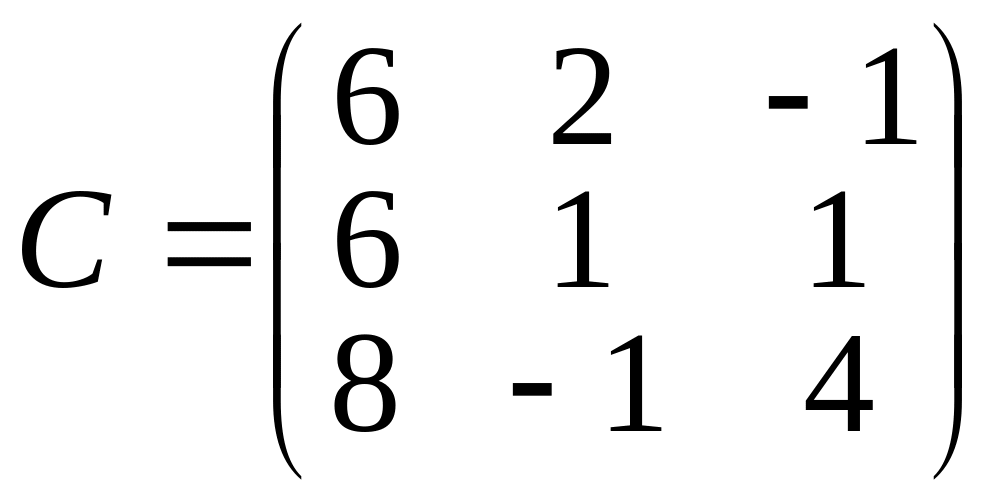Матрица, элементы главной диагонали которой равны единице, называется единичной матрицей п-го порядка и обозначается символом Е.

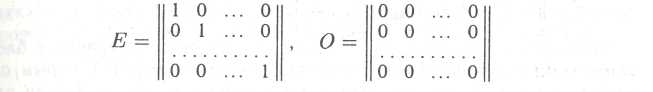
Матрица, элементы главной диагонали которой равны нулю, называется нулевой матрицей n-го порядка и обозначается символом О.

АЕ = ЕА и АО = О А.

Очевидно, что АЕ = ЕА = А, АО = ОА = О.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть A + Θ = A

Все элементы нулевой матрицы равны нулю.

Транс­понированием любой матрицы или определителя называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования.

В результате транспонирования матрицы А получается матрица, называемая транспонированной по отношению к матрице А и обозначаемая символом A^T.

Для некоторых квадратных матриц можно найти так называемую обратную матрицу.

Обратная матрица A ^{- 1} такова, что если умножить матрицу на неё, то получится единичная матрица:

AA ^{− 1} = E

Обратная матрица существует не всегда. Матрицы, для которых обратная существует, называются невырожденными (или регулярными), а для которых нет обратной матрицы  — вырожденными (или сингулярными).

Матрица невырождена, если все ее строки (столбцы) линейно независимы как векторы. Максимальное число линейно независимых строк (столбцов) называется рангом матрицы.

Квадратная матрица вырождена тогда и только тогда, когда ее определитель равен нулю.

Элементарные преобразования матриц

Элементарными преобразованиями строк матрицы называются следующие преобразования:

1. Умножение строки на число отличное от нуля,

2. Прибавление одной строки, умноженной на число, к другой строке,

3. Перестановка местами двух строк.

Элементарные преобразование столбцов матрицы определяются аналогично. При элементарных преобразованиях ранг матрицы не меняется.

Матричные операции

Сложение и вычитание допускается только для матриц одинакового размера.

Возводить в степень можно только квадратные матрицы.

• Ассоциативность сложения: A + (B + C) = (A + B) + C.

• Коммутативность сложения: A + B = B + A.

• Ассоциативность умножения: A(BC) = (AB)C.

• Умножение матриц некоммутативно: .

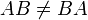• Дистрибутивность умножения относительно сложения:

A(B + C) = AB + AC;

(B + C)A = BA + CA.