
ЛР2 / Отчёт по ЛР2
.docxМинистерство науки и высшего образования РФ
ФГБОУ ВО «Кубанский Государственный Технологический Университет»
Кафедра электротехники и электрических машин
Лабораторная работа №2
«Модель асинхронного двигателя в неподвижной системе координат»
Выполнил:
ст. гр.
Проверил:
Автайкин И.Н.
Краснодар 20
Исходные данные:
P2ном = 3 кВт
U1ном = 220 В
f1ном = 50 Гц
p2 = 2
J = 0,1 кг ∙ м2
ηн = 0,82
cos φ = 0,83
Xm = 2,2 Ом
R1g = 0,078 Ом
X1g = 0,079 Ом
R2g = 0,053 Ом
X2g = 0,13 Ом
m = 3
n1 = 1500 об/мин
Скрипт для расчета параметров:
In1=(P2n)/(3*U1n*KPD*cosf); %stator rated phase current
X1t=(2*Xm0*X1g)/(Xm0+sqrt((Xm0^2)+4*Xm0*X1g)); %inductance T-shaped equivalent circuit
c=X1g/X1t; %conversion factor
R1t=R1g/c; %stator winding resistance (T-shaped)
R2t=R2g/(c^2); %rotor winding resistance (T-shaped)
X2t=X2g/(c^2); %rotor winding inductance (T-shaped)
Zbaz=U1n/In1; %Base resistance
R1=R1t*Zbaz; %stator winding resistance
R2=R2t*Zbaz; %rotor winding resistance
Xm=Xm0*Zbaz; %Inductive Magnetization Resistance
X1s=X1t*Zbaz; %Stator Scatter Resistance
X2s=X2t*Zbaz; %Rotor Scatter Resistance
X1=X1s+Xm; %Stator impedance
X2=X2s+Xm; %Rotor impedance
Lm=Xm/w0; %Magnetization loop inductance
L1s=X1s/w0; %Stator Inductance
L2s=X2s/w0; %Rotor Inductance
L1=Lm+L1s; %Total stator inductance
L2=Lm+L2s; %Total rotor inductance
sig=1-((Lm^2)/(L1*L2)); %scattering coefficient
T2=L2/R2; %Electromagnetic Rotor Time Constant
L2st=L1-((Lm^2)/L2); %The coefficient of the mathematical model
k2=Lm/L2;
r=R1+(k2^2)*R2;
T1=L2st/r;
Рисунок
1 – Модель асинхронного двигателя в
неподвижной системе координат в MATLAB
Simulink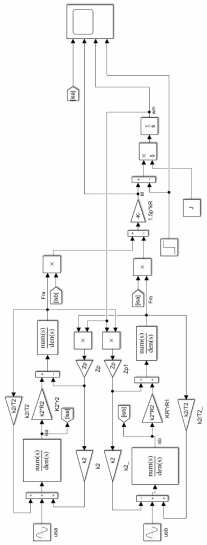

Рисунок
2 – Осциллограммы тока статора,
электромагнитного момента, скорости
ротора и момента сопротивления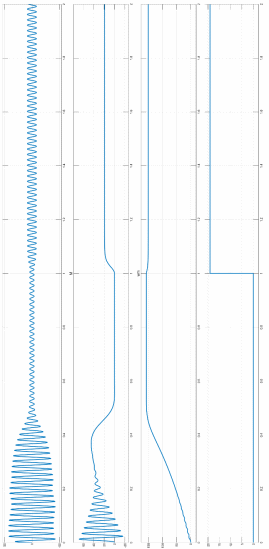
Вывод: в ходе работы в пакете MATLAB Simulink была реализована математическая модель асинхронного двигателя в неподвижной системе координат αβ. Полученные осциллограммы позволяют провести исследование переходных процессов при изменении режима работы электродвигателя.
