ЛР2 / Лабораторная работа2 (2)
.docxМОДЕЛЬ АД В НЕПОДВИЖНОЙ СИСТЕМЕ КООРДИНАТ
Основные уравнения математической
модели АД с КЗ ротором во вращающейся
с произвольной скоростью
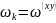 системе координат - xy
:
системе координат - xy
:
1. уравнения Кирхгофа для цепей статора и ротора:
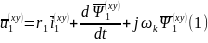
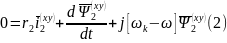
2. уравнения потокосцеплений статора и ротора:
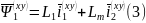
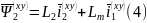
3. уравнение электромагнитного момента
в координатах (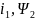 )
)
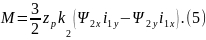
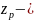 число
пар полюсов машины;
число
пар полюсов машины;
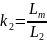
Уравнение равновесия моментов на валу машины:
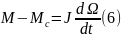
где: J (кгм2)- момент инерции на валу машины,
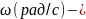 угловая частота вращения вала (ротора)
машины с количеством пар полюсов
угловая частота вращения вала (ротора)
машины с количеством пар полюсов
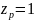 ;
;
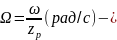 угловая частота вращения вала (ротора)
машины c определенным
количеством пар полюсов
угловая частота вращения вала (ротора)
машины c определенным
количеством пар полюсов
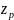 ;
;
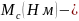 момент
сопротивления рабочего механизма
момент
сопротивления рабочего механизма
Для реализации модели АД в программном
комплексе Mathlab simulink
необходимо уравнения (1-2) выразить
относительно какой-то одной произвольной
пары векторов (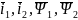 ).
Так как в рассматриваемом случае
уравнение момента (5) разрешено относительно
тока статора
).
Так как в рассматриваемом случае
уравнение момента (5) разрешено относительно
тока статора
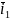 и потокосцепления ротора
и потокосцепления ротора
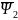 то методом исключения добьемся
поставленной задачи.
то методом исключения добьемся
поставленной задачи.
В последующих преобразованиях будем
опускать верхний индекс системы координат
- (xy). Преобразуем
уравнения (1), (2) через
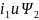 методом исключения. Для этого из уравнения
(4) выразим
методом исключения. Для этого из уравнения
(4) выразим
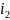
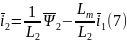
Подставим в уравнение (3):
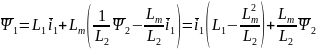
Введем коэффициенты
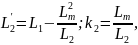
тогда
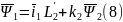
Из уравнения (2) исключим
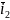 .
Для этого подставим (7) в (2).
.
Для этого подставим (7) в (2).
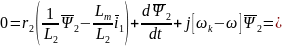
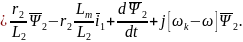
Обозначим
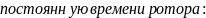
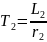
тогда:
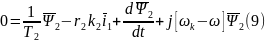
Из уравнения (9) выразим
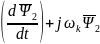 , которое в дальнейшем подставим в
уравнение (1).
, которое в дальнейшем подставим в
уравнение (1).
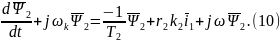
Подставим в (1) уравнение (6)
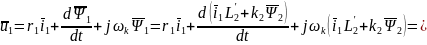
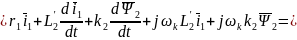
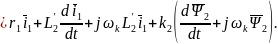
С учетом (8)
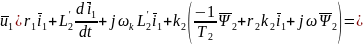
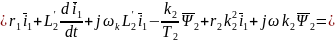
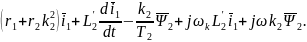
Обозначим
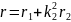 , тогда:
, тогда:
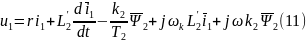
Полученные уравнения напряжений ротора
(9) и статора (11), выраженные через
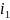 и
и
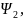 запишем в систему
запишем в систему
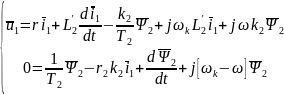
Вещественную ось обозначим x, а мнимую через y. Пространственные векторы в этом случае раскладываются по осям:
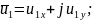
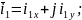
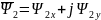 .
.
Подставим эти значения в уравнения (9), (11)
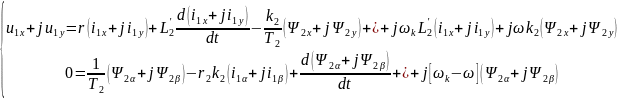
Разделив отдельно вещественные и мнимые части, получим:
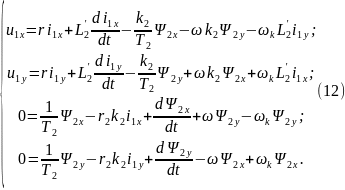
Преобразуем (12) в операторную форму,
заменив
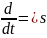 :
:
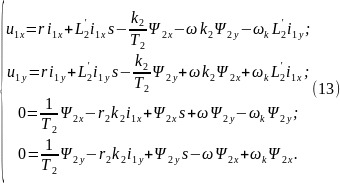
Для создания модели, из системы уравнений (13) выражаются токи и потокосцепления и система уравнений, для произвольно-вращающейся системы координат с учетом электромагнитного момента и уравнения вращения, примет вид:
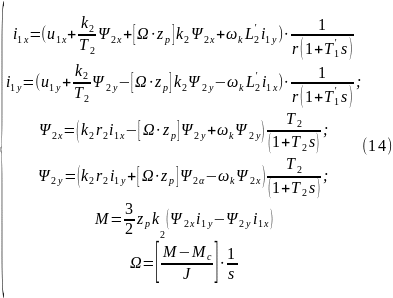
где:
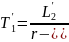 постоянная
времени статора;
постоянная
времени статора;
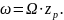
Математическую модель АД, представленную
в СК xy,
(14) можно преобразовать для любых других
СК, подставив соответствующие значения
частоты вращения СК -
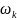 :
:
- для СК (αβ)
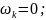
- для СК - (dq)
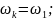
- для СК - (uv)
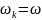 .
.
Реализация математической модели АД в Mathlab simulink
Наибольший интерес представляют модели АД в СК - αβ. Преобразуем систему уравнений (13) для СК - αβ.
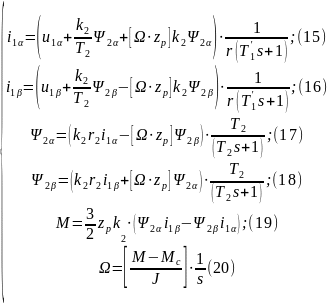
Структурные схемы
Реализация ситемы уравнений (15)-(20) осуществляется среде Simulink в виде структурных схем
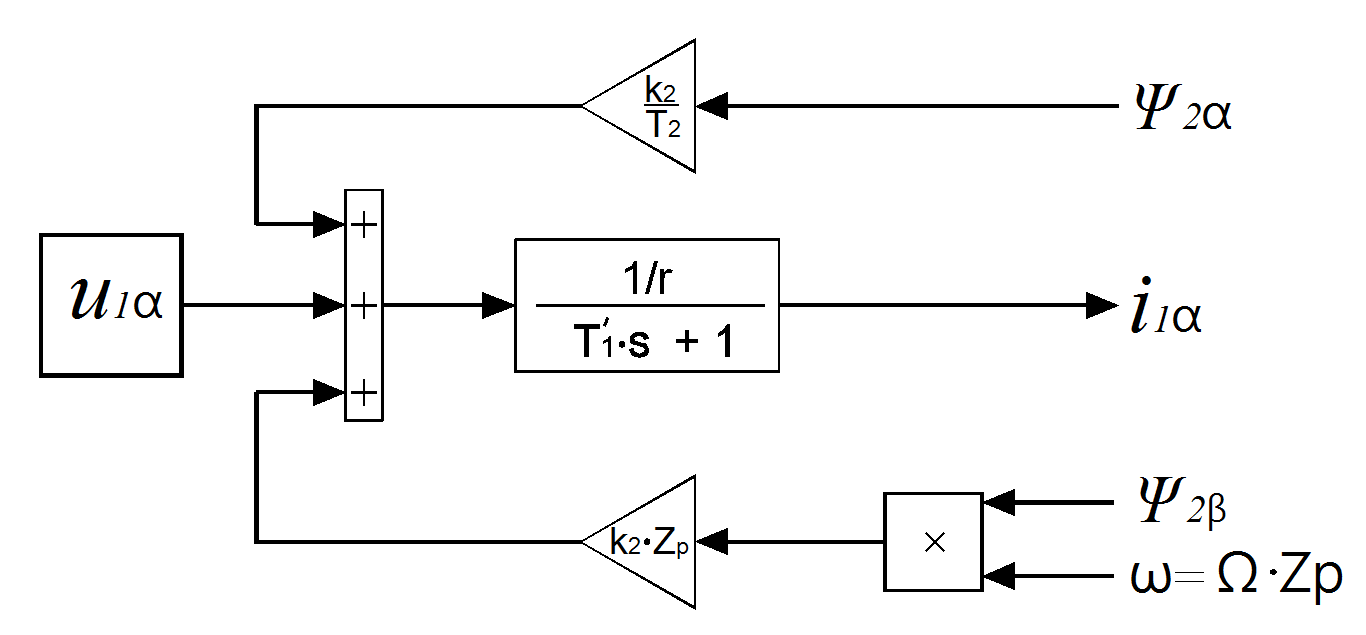
Рисунок 1 - Структурная схема определения
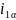 для уравнения (15)
для уравнения (15)
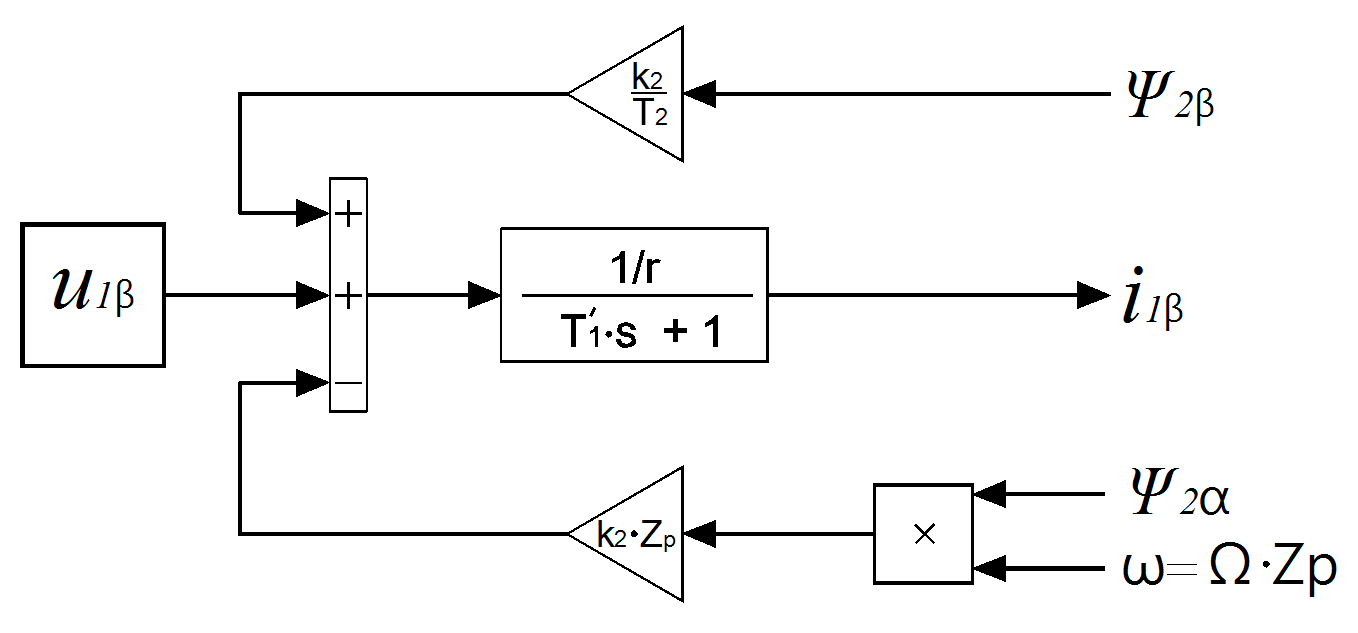
Рисунок 2 - Структурная схема определения
 для уравнения (16)
для уравнения (16)
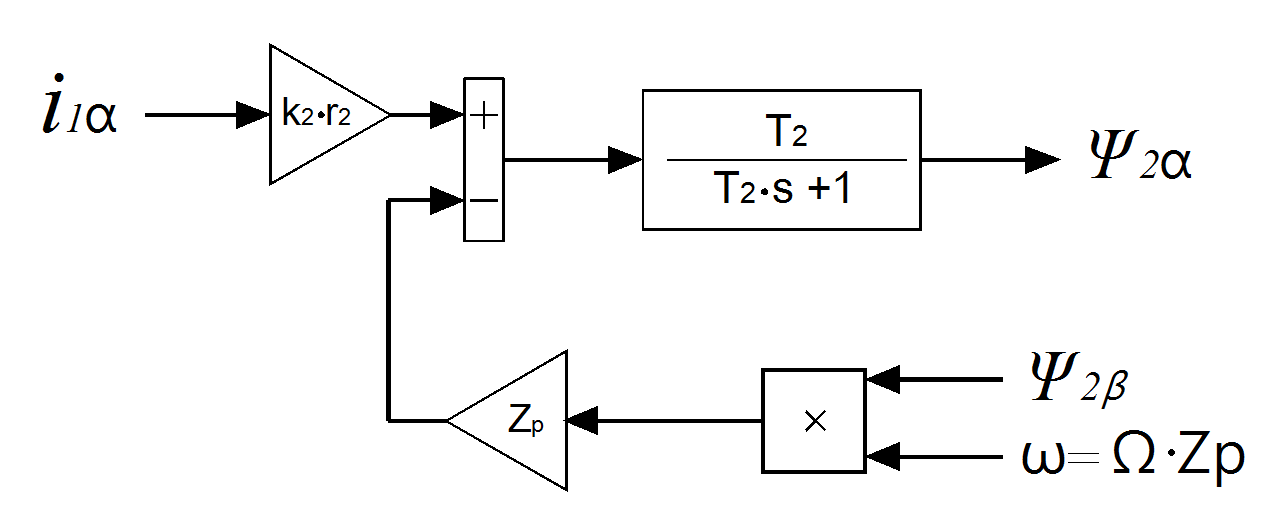
Рисунок 3 - Структурная схема определения
 для уравнения (17)
для уравнения (17)
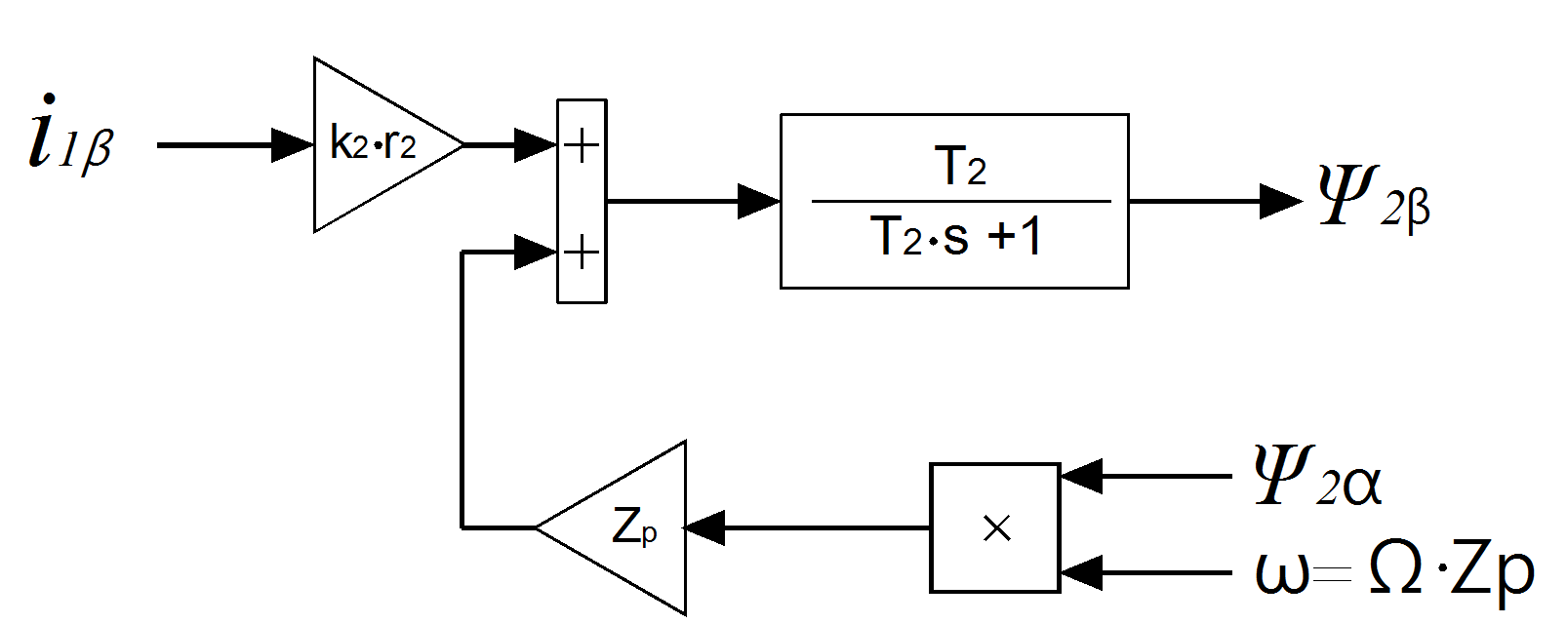
Рисунок 4 - Структурная схема определения
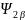 для уравнения (18)
для уравнения (18)
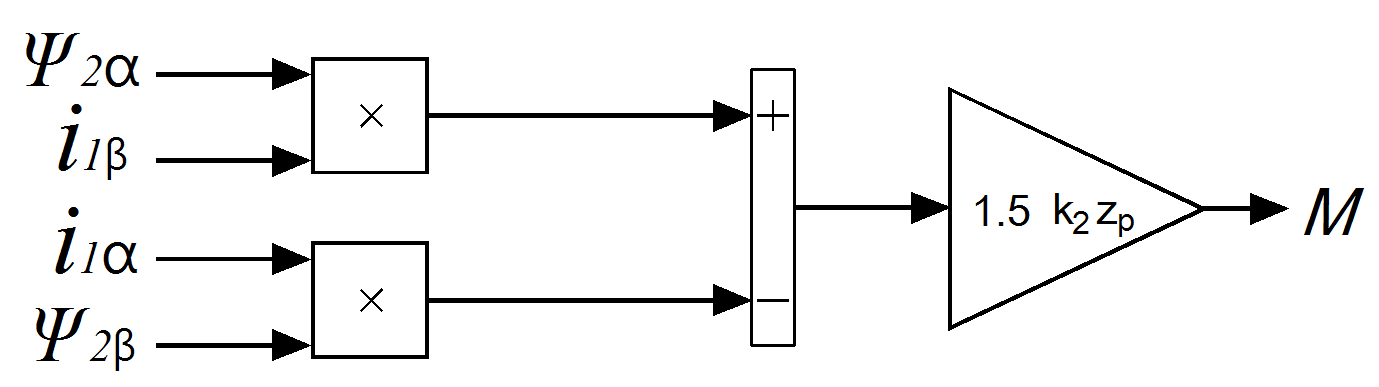
Рисунок 5 - Структурная схема определения
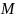 для уравнения (19)
для уравнения (19)
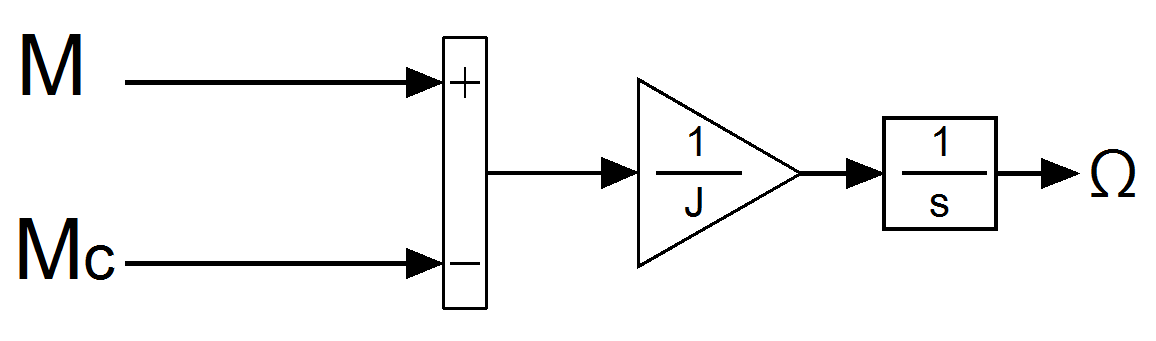
Рисунок 6 - Структурная схема определения
 для уравнения (20)
для уравнения (20)
|
Блоки |
Настраиваемые параметры |
1 |
u1α, u1β
|
Название блока - Sine Wave (Sources) Amplitude
- амплитуда сигнала, для данной схемы
Frequency
– угловая частота колебаний, для
данной схемы равная
Phase
– начальная фаза ( |
2 |
|
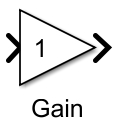
Название блока - Gain (Math Operations) - осуществляет умножение входного сигнала на постоянную величину, значение которой задаётся в настройке блока. Gain
– коэффициент усиления
|
3 |
|
Название блока - Sum (Math Operations) - суммирует поступающие на него сигналы. Iconshape – форма изображения (круг или прямоугольник), Listofsigns – список входов и их знаки. |
4 |
|
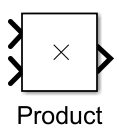
Название блока - Product (Math Operations) - выполняет умножение (деление) входных сигналов. Numberofinputs – количество входов, Multiplication – тип способа умножения |
5 |
|
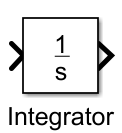
Название блока - Integrator (Continuous) - представляет идеальное интегрирующее звено. Он позволяет осуществить интегрирование поступающего на него сигнала в непрерывном времени. |
6 |
|
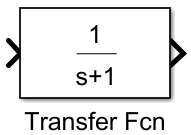
Название блока - Transfer Fcn (Continuous) - реализует звено введённой в него передаточной функции:
Numerator
– числитель, для данной схемы числовое
значение результата деления -
Denominator [Ti 1] – знаменатель, для данной схемы первое значение - Ti (постоянная времени), а второе - 1.
|
7 |
|
Название блока - Scope (Sinks) Numberofaxes – количество осей, Timerange – интервал времени, Ticklabels – метки осей.
|
8 |
|
Название блока - Step (Sources). Моделирует ступенчатую нагрузку на валу машины. Step time - время перехода от начального значения к финальному; Initial value - начальное значение (нагрузки); Final value - финальное значение (нагрузки).
|
9 |
|
Название блока - Goto Блок передачи сигнала (Signal Routing). Блок выполняет передачу сигнала к блоку From. Использование блока Goto совместно с блоком From обеспечивает передачу сигнала без линии связи. Tag – Идентификатор сигнала. Tag visibility – Признак видимости. Выбирается из списка:
|
10 |
|
Название блока - From Блок приема сигнала (Signal Routing). Блок выполняет прием сигнала от блока Goto.
|
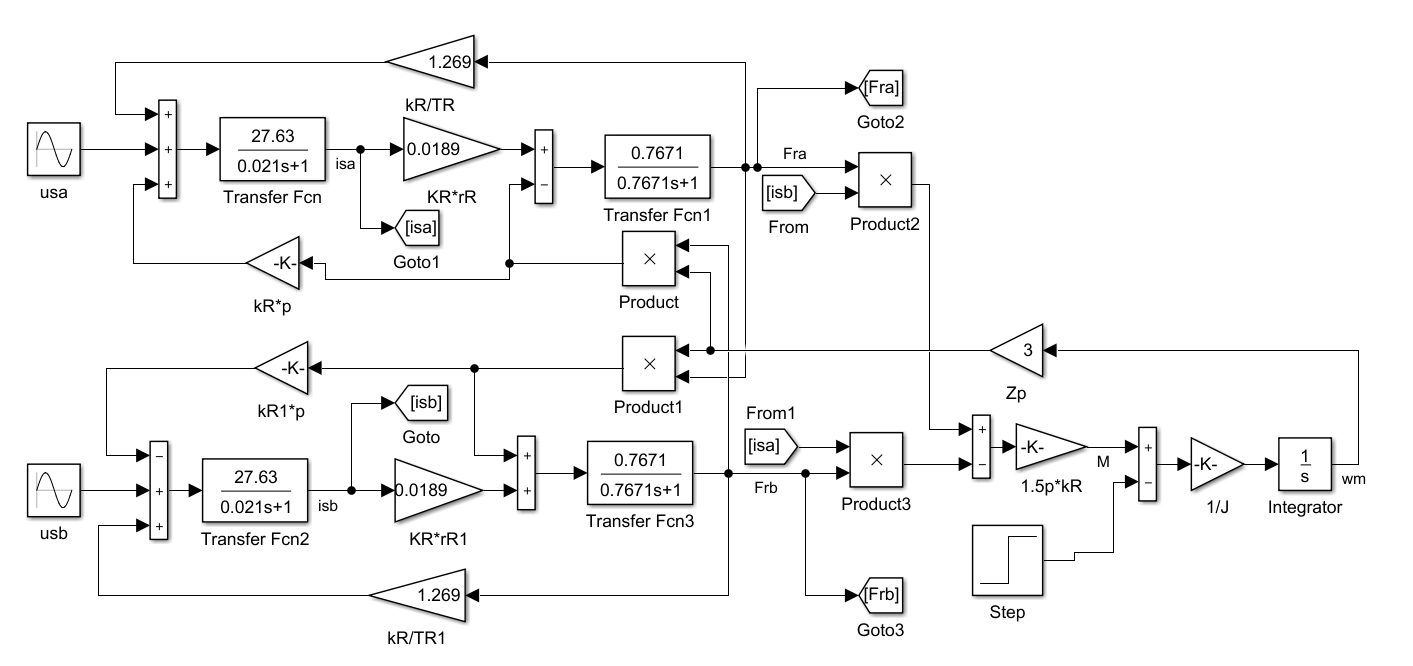
Рисунок 7 - Структурная схема АД, реалиующая смстему уравнений (16)-(20)

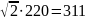 В,
В,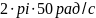 ,
,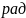 ),
),
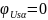
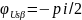
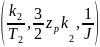
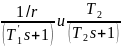
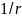 ,
,