ЛР5_Шакиров_Айдар_МО-217

ФГБОУ ВО

Уфимский Государственный Авиационный Технический Университет

Кафедра ВМиК

Отчет по лабораторной работе №5

«Нахождение эйлерова цикла в графе»

по дисциплине

«Структуры и алгоритмы компьютерной обработки данных»

Выполнил:

студент группы МО-217

Шакиров Айдар Рушанович

Проверила:

Канд. техн. наук, доцент

Верхотурова Галина Николаевна

Уфа 2020

Постановка задачи:

Найти эйлеров цикл в заданном графе.

Теория

Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу.

Эйлеров путь в графе существует тогда и только тогда, когда граф связный и содержит не более чем 2 вершины нечетной степени.

Если в связном графе нет вершин нечетной степени, то каждый эйлеров путь называется циклом.

Алгоритм нахождения эйлерова цикла графа

1. Если алгоритм обхода в глубину не посетил все вершины, то

   1. Выводим сообщение «Граф не содержит эйлерова цикла, так как граф несвязный».

2. Иначе

   1. Если количество ребер каждой какой-либо вершины нечетное, то

      1. Выводим сообщение «Граф не содержит эйлерова цикла, так как не все вершины имеют четную степень».

   2. Иначе

      1. Заносим первую вершину во временный стек.

      2. Пока временный стек не пустой:

         1. Присваиваем временной вершине значение вершины стека.

         2. Если количество ребер временной вершины больше нуля, то

            1. Заносим во временный стек первую смежную вершину.

            2. Удаляем ребро, соединяющую временную вершину и ее первую смежную вершину.

         3. Иначе

            1. Вынимаем из временного стека и заносим в стек эйлерова цикла.

         4. Выводим эйлеров цикл на экран

Входные данные:

• vertices[] – массив вершин графа.

• edges[] – массив ребер графа.

Промежуточные данные:

• stack – стек для промежуточного хранения вершин.

• cycl – стек для хранения вершин эйлерова пути.

• node – переменная для временного хранения вершины.

• adjacent – переменная для временного хранения первой смежной вершины.

Выходные данные:

• statusCycl– текстовое поле для вывода последовательности вершин эйлерова цикла.

• cycl – стек для хранения вершин эйлерова пути графа.

Реализация алгоритма нахождения эйлерова цикла графа

private void EulerianPath(IList<Vertice> vertices)

O(n³)

{

if(!DepthFirstSearch (vertices, false))

{

statusCycl.Text = "Граф не содержит эйлерова цикла, так как граф несвязный";

}

else

{

//проверка четности вершин

foreach(var v in vertices)

{

if (v.Edges.Count % 2 != 0)

O(n)

{

statusCycl.Text = "Граф не содержит эйлерова цикла, так как не все вершины имеют четную степень";

return;

}

}

var stack = new Stack<Vertice>();

var cycl = new Stack<Vertice>();

stack.Push(vertices[0]);

Vertice node;

while (stack.Count > 0)

O(n³)

{

O(n)

node = stack.Peek();

var nodeEdges = new List<Edge>(node.GetNotDeletedEdges());

if (nodeEdges.Count() > 0)

{

O(n²)

var adjacent = nodeEdges[0].GetLinkVertice(node);

stack.Push(adjacent);

nodeEdges[0].isDeleted = true;

}

else

{

cycl.Push(stack.Pop());

}

}

O(n)

foreach (var e in edges)

O(n)

e.isDeleted = false;

ShowCycl(cycl);

}

}

Оценка сложности:

Сложность алгоритма нахождения эйлерова цикла графа составляет O(n³).

Если не проверять граф на связность, то сложность алгоритма составит O(n²).

Результат:

• Несвязный граф

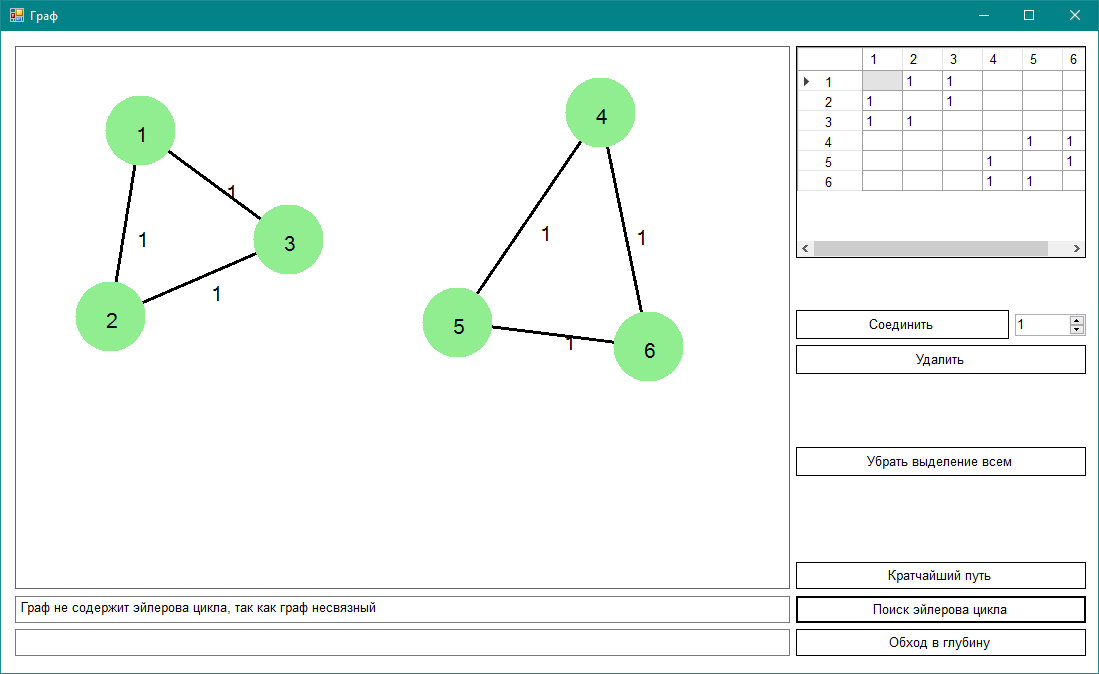
Проверяем граф на связность. Алгоритм обхода в глубину прошел 3 из 6 вершин. Граф несвязный.

Граф не содержит эйлерова цикла, так как граф несвязный.

• Граф, у которого не все вершины имеют четную степень

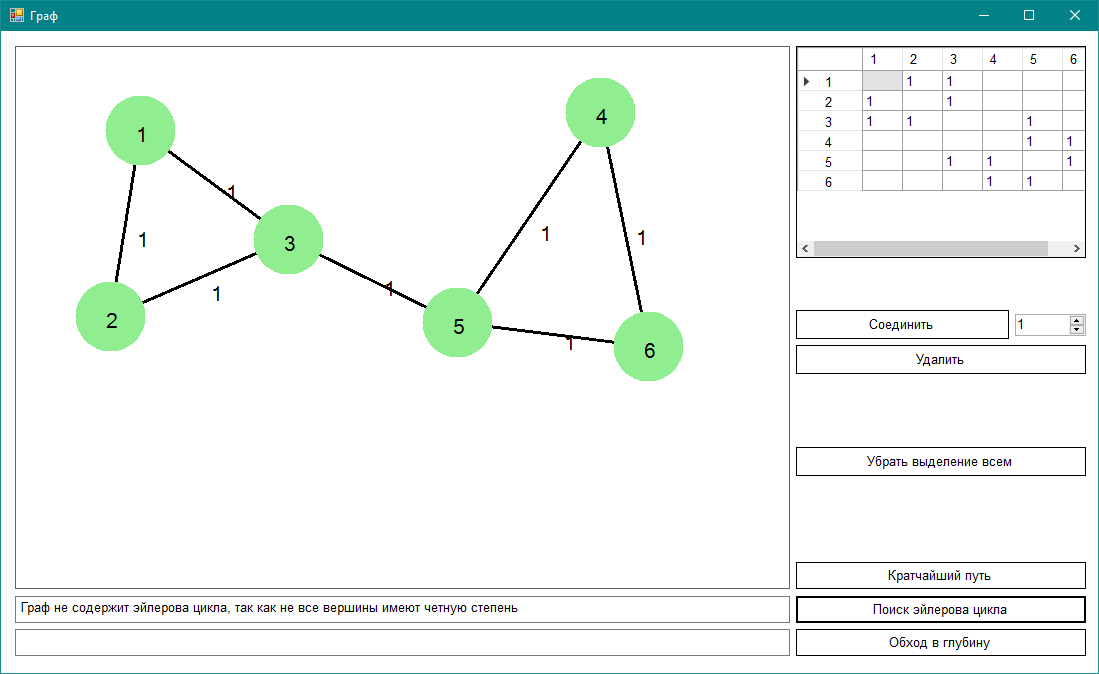
Проверяем граф на связность. Алгоритм обхода в глубину прошел 6 из 6 вершин. Граф связный.

Проверяем вершины на четность смежных вершин. У вершины (3) нечетное количество ребер.

Граф не содержит эйлерова цикла, так как не все вершины имеют четную степень.

• Граф, содержащий эйлеров цикл

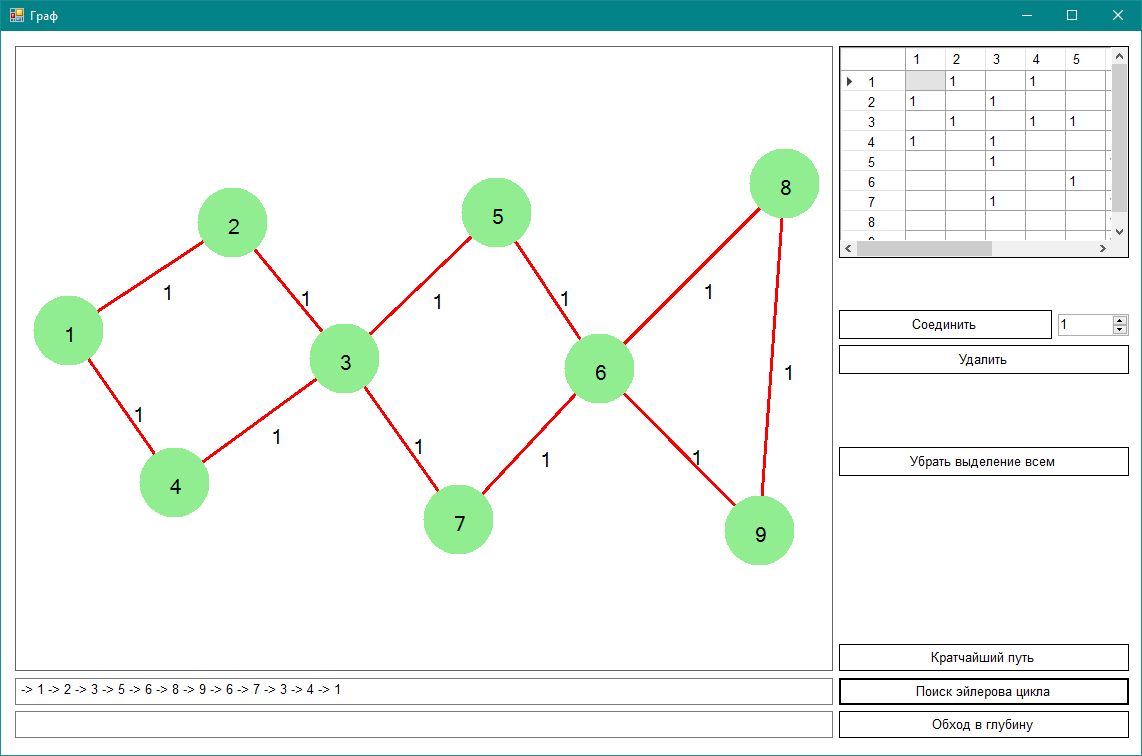
Проверяем граф на связность. Алгоритм обхода в глубину прошел 6 из 6 вершин. Граф связный.

Проверяем вершины на четность смежных вершин. Все вершины имеют четную степень.

Начинаем поиск эйлерового цикла.

Помещаем во временный стек начальную вершину (1).

Пока временный стек не пустой:

У вершины стека (1) находим первую смежную вершину (2), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [2, 1]

У вершины стека (2) находим первую смежную вершину (3), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [3, 2, 1]

У вершины стека (3) находим первую смежную вершину (4), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [4, 3, 2, 1]

У вершины стека (4) находим первую смежную вершину (1), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [1, 4, 3, 2, 1]

Вершина стека (1) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [1].

Вершина стека (4) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [4, 1].

У вершины стека (3) находим первую смежную вершину (5), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [5, 3, 2, 1]

У вершины стека (5) находим первую смежную вершину (6), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [6, 5, 3, 2, 1]

У вершины стека (6) находим первую смежную вершину (7), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [7, 6, 5, 3, 2, 1]

У вершины стека (7) находим первую смежную вершину (3), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [3, 7, 6, 5, 3, 2, 1]

Вершина стека (3) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [3, 4, 1].

Вершина стека (7) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [7, 3, 4, 1].

У вершины стека (6) находим первую смежную вершину (8), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [8, 6, 5, 3, 2, 1]

У вершины стека (8) находим первую смежную вершину (9), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [9, 8, 6, 5, 3, 2, 1]

У вершины стека (9) находим первую смежную вершину (6), заносим ее во временный стек. Ребро, соединяющее эти вершины, удаляем из графа. Временный стек: [6, 9, 8, 6, 5, 3, 2, 1]

Вершина стека (6) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [6, 7, 3, 4, 1].

Вершина стека (9) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [9, 6, 7, 3, 4, 1].

Вершина стека (8) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [8, 9, 6, 7, 3, 4, 1].

Вершина стека (6) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [6, 8, 9, 6, 7, 3, 4, 1].

Вершина стека (5) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [5, 6, 8, 9, 6, 7, 3, 4, 1].

Вершина стека (3) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [3, 5, 6, 8, 9, 6, 7, 3, 4, 1].

Вершина стека (2) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [2, 3, 5, 6, 8, 9, 6, 7, 3, 4, 1].

Вершина стека (1) не имеет смежных вершин. Вынимаем ее из временного стека и помещаем в стек, хранящий эйлеров цикл [1, 2, 3, 5, 6, 8, 9, 6, 7, 3, 4, 1].

Эйлеров цикл: 1 - 2 - 3 - 5 - 6 - 8 - 9 - 6 - 7 - 3 - 4 - 1.

Список литературы:

1. Вирт, Н. Алгоритмы и структуры данных. Новая версия для Оберона : учебное пособие / Н. Вирт. — Москва : ДМК Пресс, 2010 — 272 с.