ЛР4_Шакиров_Айдар_МО-217

ФГБОУ ВО

Уфимский Государственный Авиационный Технический Университет

Кафедра ВМиК

Отчет по лабораторной работе №4

«Поиск в глубину в графе»

по дисциплине

«Структуры и алгоритмы компьютерной обработки данных»

Выполнил:

студент группы МО-217

Шакиров Айдар Рушанович

Проверила:

Канд. техн. наук, доцент

Верхотурова Галина Николаевна

Уфа 2020

Постановка задачи:

Задан граф. Осуществить прохождение вершин заданного графа в соответствии с обходом этого графа согласно алгоритму «Поиск в глубину» в порядке возрастания первоначальной нумерации вершин графа.

Алгоритм прохождения вершин графа

1. Заносим в стек первую вершину.

2. Заносим в список посещенных первую вершину.

3. Выделяем визуально первую вершину.

4. Пока количество элементов в стеке больше нуля:

   1. Текущей вершине приравниваем вершину стека.

   2. Перебираем все вершины графа:

      1. Если эта вершина имеет общее ребро с текущей и эта вершина не содержится в списке посещенных, то

         1. Заносим эту вершину в стек.

         2. Заносим эту вершину в список посещенных.

         3. Выделяем визуально ребро, соединяющее текущую и эту вершину.

         4. Выделяем визуально эту вершину.

   3. Если у текущей вершины нет смежных вершин, то

      1. Удаляем вершину стека.

Входные данные:

• vertices[] – массив вершин графа.

• edges[] – массив граней графа.

Вспомогательные данные:

• vertices – список вершин графа.

• stack – стек для промежуточного хранения вершин графа.

• visited – список посещенных вершин графа.

• node – переменная для временного хранения вершины графа.

Выходные данные:

• statusObhod – текстовое поле для вывода последовательности прохождения графа.

Реализация алгоритма прохождения вершин графа

private bool DepthFirstSearch(IList<Vertice> vertices)

{

var stack = new Stack<Vertice>();

var visited = new List<Vertice>();

stack.Push(vertices[0]);

visited.Add(vertices[0]);

if (isVisit)

VisitNode(vertices[0], isShow);

Vertice node;

while (stack.Count > 0)

{

node = stack.Peek();

bool flag = false;

O(n)

for (int i = 0; i < vertices.Count; i++)

if (node.HasLink(vertices[i]) && !visited.Contains(vertices[i]))

{

visited.Add(vertices[i]);

O(n³)

stack.Push(vertices[i]);

O(n²)

if (isVisit)

{

VisitEdge(node, vertices[i], isShow);

VisitNode(vertices[i], isShow);

}

flag = true;

break;

}

if(!flag)

stack.Pop();

}

}

Оценка сложности:

Сложность алгоритма прохождения вершин согласно алгоритму «поиска в глубину» составляет O(n³).

Результат:

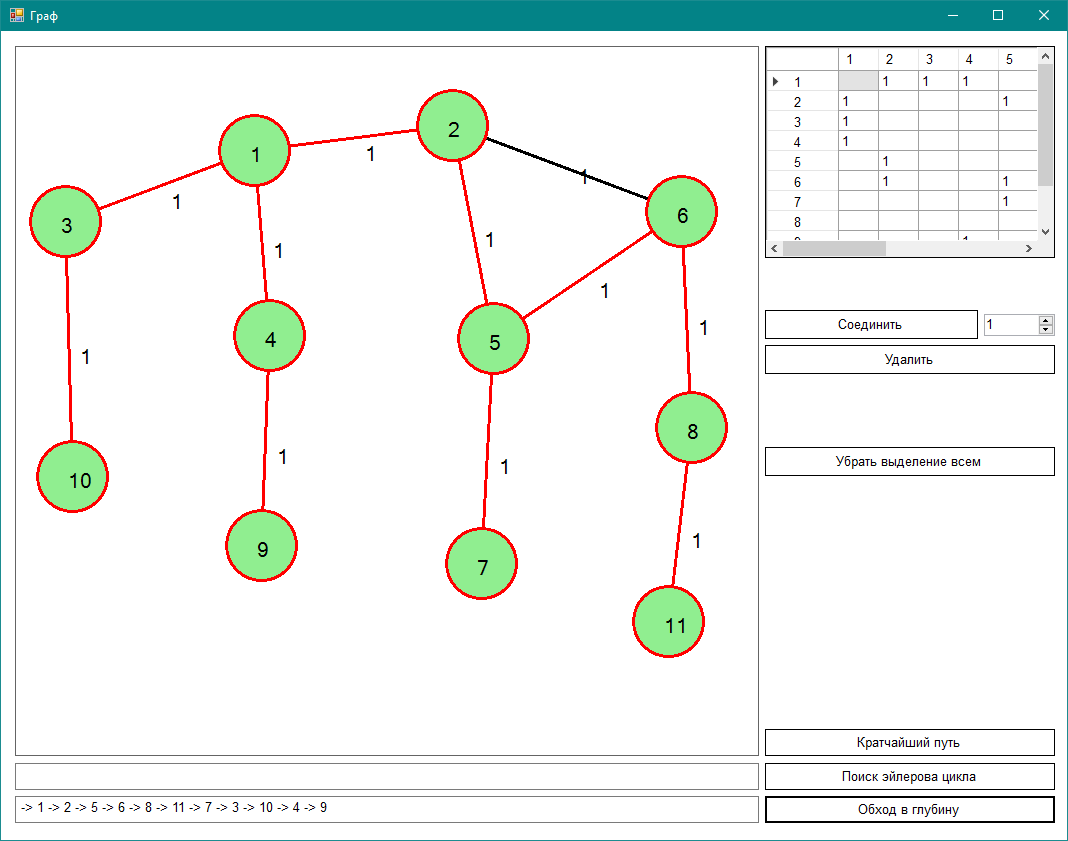
Ход работы:

Помещаем вершину 1 в стек и помечаем ее как посещенную.

Пока стек не пустой:

У вершины стека (1) находим первую смежную вершину (2), заносим в стек и помечаем как посещенную. Текущий стек: [2, 1]

У вершины стека (2) находим первую смежную вершину (5), заносим в стек и помечаем как посещенную. Текущий стек: [5, 2, 1]

У вершины стека (5) находим первую смежную вершину (6), заносим в стек и помечаем как посещенную. Текущий стек: [6, 5, 2, 1]

У вершины стека (6) находим первую смежную вершину (8), заносим в стек и помечаем как посещенную. Текущий стек: [8, 6, 5, 2, 1]

У вершины стека (8) находим первую смежную вершину (11), заносим в стек и помечаем как посещенную. Текущий стек: [11, 8, 6, 5, 2, 1]

Вершина стека (11) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [8, 6, 5, 2, 1]

Вершина стека (8) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [6, 5, 2, 1]

Вершина стека (6) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [5, 2, 1]

У вершины стека (5) находим первую смежную вершину (7), заносим в стек и помечаем как посещенную. Текущий стек: [7, 5, 2, 1]

Вершина стека (7) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [5, 2, 1]

Вершина стека (5) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [2, 1]

Вершина стека (2) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [1]

У вершины стека (1) находим первую смежную вершину (3), заносим в стек и помечаем как посещенную. Текущий стек: [3, 1]

У вершины стека (3) находим первую смежную вершину (10), заносим в стек и помечаем как посещенную. Текущий стек: [10, 3, 1]

Вершина стека (10) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [3, 1]

Вершина стека (3) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [1]

У вершины стека (1) находим первую смежную вершину (4), заносим в стек и помечаем как посещенную. Текущий стек: [4, 1]

У вершины стека (4) находим первую смежную вершину (9), заносим в стек и помечаем как посещенную. Текущий стек: [9, 4, 1]

Вершина стека (9) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [4, 1]

Вершина стека (4) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: [1]

Вершина стека (1) не имеет непосещенных смежных вершин, соответственно вынимаем ее из стека. Текущий стек: []

Стек пуст. Завершаем алгоритм. Было посещено 11 из 11 вершин.

Список литературы:

1. Вирт, Н. Алгоритмы и структуры данных. Новая версия для Оберона : учебное пособие / Н. Вирт. — Москва : ДМК Пресс, 2010 — 272 с.