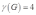11._._3_
.docxПЗ 11. Графы. Метод Магу (часть 3)
Множества вершин, которые одновременно являются внешне и внутренне устойчивыми называются ядром графа. В графе может быть несколько ядре, могут быть они разного размера, а может и не быть вовсе.
Алгоритм Магу для определения множества внутренней устойчивости.
Шаг 1. Построить матрицу смежности вершин графа.
Шаг 2. По единицам матрицы смежности построить парные дизъюнкты.
Шаг 3. Получить ДНФ.
Шаг 4. Для каждой конъюнкции выписать недостающие вершины. Это и будут множества внутренней устойчивости.
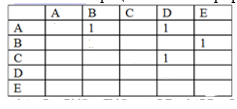
Пример. Найти множество внутренней устойчивости для графа.(Алгоритм) |
|
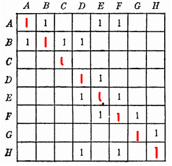
Шаг 1. Ориентированный граф и его матрица смежности
|
Шаг 2. Строим парные дизъюнкты по единицам матрицы смежности. (A v B)(A v D)(B v E)(C v D) Шаг 3. Приводим к ДНФ (A v B)(A v D)(B v E)(C v D)=(A v BD)(BC v EC v BD v ED)= ABC v AEC v ABD v AED v BCD v BDEC v BD v BDE=ABC v ACE v ADE v BD Шаг 4. Для каждой конъюнкции выписываем недостающие вершины. {D,E},{B,D},{B,C},{A,C,E} |
Алгоритм Магу для определения множества внешней устойчивости.
Шаг 1. Построить матрицу смежности вершин графа G.
Шаг 2. Поставить единицы по диагонали матрицы смежности.
Шаг 3. Выписать дизъюнкты по единицам и получить ДНФ.
Пример. Найти множество внешней устойчивости графа. (Алгоритм) |
|
Шаг 1 и 2. Матрица смежности графа, по диагонали 1.
|
Шаг 3. Выписываем дизъюнкты по единицам и получаем ДНФ. (A v B v D)(B v E)(C v D)DE=ABCDE v ABDE v ACDE v ADE v BCDE v BDE v BCDE v BDE v DBCE v DBE v DEC v DE = DE {D,E} – множество внешней устойчивости, вершины A,B,C имеют дуги в Е и D. В данном графе {D,E} - ядро |
Найдём для этого же графа множество внутренней устойчивости |
|
Шаг 1. Матрица смежности (убрали 1 по диагонали)
|
Шаг 2 и 3. Строим парные дизъюнкты по единицам матрицы смежности. (A v B)(A v D)(B v E)(C v D) = ABC v ABD v ACE v AED v ADBC v ADB v ADEC v ADE v ABC v BD v BCE v BED v DBC v DB v BDEC v BDE= ACE v ADE v ABC v BD Шаг 4. Для каждой конъюнкции выписываем недостающие вершины. {B,D},{B,C},{D,E},{A,C,E} Мы доказали, что D,E - ядро графа. |
Пример 20. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.Найдем множества внутренней устойчивости:
(1v3)(1v4)(2v4)(2v5)(3v5) Перейдем к ДНФ 123v125v145v234v345 Для каждой конъюнкции выписываем недостающие вершины, образующие множества внутренней устойчивости. {4,5},{3,4},{2,3},{1,5},{1,2} Наибольшее из них – число внутренней устойчивости. |
2.Найдем множества внешней устойчивости:
(1v3)(2v4)(3v5)(1v4)(2v5) Перейдем к ДНФ 123v125v145v234v345 {1,2,3}{1,2,5},{1,4,5},{2,3,4},{3,4,5} Наименьшее из них – число внешней устойчивости |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 28. Используя метод Магу, определить максимально внутренне устойчивые, а также минимально внешне устойчивые множества вершин орграфов и найти их ядра. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
1.Найдем множества внутренней устойчивости:
(1v2)(1v3)(2v3)(3v4) Перейдем к ДНФ 13v23v124 Для каждой конъюнкции выписываем недостающие вершины, образующие множества внутренней устойчивости. {2,4},{1,4},{3} Наибольшее из них – число внутренней устойчивости. |
2.Найдем множества внешней устойчивости:
(1v2v3)(2)(2v3v4)(3v4) Перейдем к ДНФ 23v24 Множества внешней устойчивости: {2,3},{2,4} Наименьшее из них – число внешней устойчивости {2,4} - ядро графа. |
||||||||||||||||||||||||||||||||||||||||||||||||||
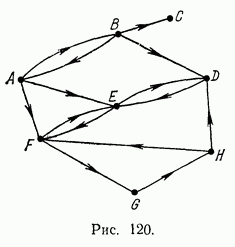
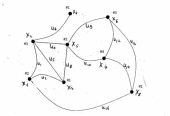
Пример И.1.
|
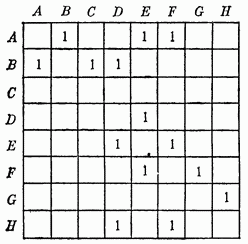
Построим булеву матрицу графа
|
Найдем множества внутренней устойчивости:
!!! + = v
|
Для каждой конъюнкции выписываем недостающие вершины, образующие множества внутренней устойчивости. Таким образом, граф обладает восемью максимальными внутренне устойчивыми подмножествами: {C,D,F},{B,F},{B,E,G},{B,E,H},{C,E,G},{C,E,H},{A,C,D,G},{A,C,H}. Наибольшее из них – число внутренней устойчивости.(4) |
||
Найдем множества внешней устойчивости:
(A v B v E v F)(A v B v C v D)C(D v E)(D v E v F)(E v F v G)(G v H)(D v F v H)= =(A v B v CE v DE v CF v DF)C(D v E)(EH v FH v G)=( A v B v CE v DE v CF v DF)C(DFH v DG v EH v EG)= ACDFH+BCDFH+CDEFH+CDEFH+CDFH+CDFH+ACDG+BCDG+CDEG+CDEG+CDFG+CDFG+ACEH+BCEH+CEH+CDEH+CFEH+CDFEH+ACEG+BCEG+CEG+CDEG+CFEG+CDFEG = CDFH+ACDG+BCDG + CDFG+ CEH + CEG ДНФ: Фs= CDFH+ACDG+BCDG + CDFG+ CEH + CEG=1 Множества внешней устойчивости: {C,D,F,H}, {A,C,D,G}, {B,C,D,G}, {C,D,F,G}, {C,E,H}, {C,E,G} {A,C,D,G},{C,E,H}, {C,E,G} – ядра графа. |
||
Хромати́ческое число́ гра́фа G — минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета. Обычно обозначается χ(G).
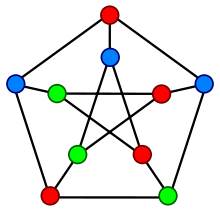
Алгоритм Магу для определения хроматического числа графа. Раскраска графа
Шаг 1. Построить матрицу инцидентности графа G.
Шаг 2. Выписать дизъюнкты по единицам для столбцов матрицы и получить ДНФ.
Шаг 3. Для каждой конъюнкции выписать недостающие вершины до полной системы образующих.
Шаг 4. Упорядочить полученные множества вершин в порядке убывания их кардинальных чисел.
Шаг 5. Припишем вершинам первого множества цвет «1». Удалим раскрашенные вершины из всех множеств и оставшиеся множества упорядочим в порядке убывания их мощности.
Припишем вершинам следующего множества цвет «2». Удалим раскрашенные вершины из всех множеств и оставшиеся множества упорядочим в порядке убывания их мощности.
Продолжаем данную итерацию, пока множество подмножеств не окажется пустым.
Количество цветов, использованных при раскраске графе является хроматическим числом.
Пример раскраски графа по алгоритму Магу-Вейсмана. С помощью алгоритма Магу—Вейсмана выполнить правильную раскраску вершин графа с минимальным количеством цветов. |
|
Начальный граф:
Скелет графа: Убрали повторяющиеся ребра
Раскраска графа
|
Шаг 1. Построить матрицу инцидентности графа G.
Шаг 2. Выписать дизъюнкты по единицам для столбцов матрицы и получить ДНФ. P=(x1+x2)(x1+x3)(x2+x3)(x2+x4)(x3+x5)(x5+x6)(x5+x7)(x6+x7)(x6+x8)(x7+x8) (x1+x8) = (x1+x2x3x8)(x2+x3x4)(x5+x3x6x7)(x6+x7x8)(x7+x8)= =(x1x2+x1x3x4+x2x3x8+x2x3x4x8)(x5x6+x3x6x7+x5x7x8+x3x6x7x8)(x7+x8)= =(x1x2+x1x3x4+x2x3x8)(x5x6+x3x6x7+x5x7x8)(x7+x8)= =(x1x2+x1x3x4+x2x3x8)(x5x6x7+x3x6x7+x5x7x8+x5x6x8+x3x6x7x8+x5x7x8)= =(x1x2+x1x3x4+x2x3x8)(x5x6x7+x3x6x7+x5x7x8+x5x6x8)= =(12567+134567+235678+12367+13467+23678+12578+134578+23578+12468+134568+23568)= =(x1x2x5x6x7+x1x2x3x6x7+x1x3x4x6x7+x2x3x6x7x8+x1x2x5x7x8 +x1x3x4x5x7x8 +x2x3x5x7x8+x1x2x4x6x8+x1x3x4x5x6x8+x2x3x5x6x8) Шаг 3. Для каждой конъюнкции выписать недостающие вершины до полной системы образующих. x3x4x8, x4x5x8, x2x5x8, x1x4x5, x3x4x6, x2x6, x1x4x6, x3x5x7, x2x7, x1x4x7 Получили полный обзор всех максимальных пустых подграфов графа G. Шаг 4. Упорядочить полученные множества вершин в порядке убывания их кардинальных чисел. (количество элементов множества) x3x4x8, x4x5x8, x2x5x8, x1x4x5, x3x4x6, x1x4x6, x3x5x7, x1x4x7, x2x6, x2x7
Определяем хроматическое число γ(G) графа G.
Шаг 5.
x2x5, x1x5, x1x6, x5x7, x1x7, x2x6, x2x7, x5, x6
x1x6, x1x7, x7, x6, x1
x7
Осталось пустое множество.
Всё.
Хроматическое число графа:
|