ПЗ
10. Графы (часть 2)
Инварианты
графа. Число вершин. Число ребер. Число
граней. Остовное дерево. Толщина.
Независимое множество. Клика и плотность
графа. Граф дополнения. Число доминирования.
9.1.
Инварианты графа
Два
графа называются изоморфными,
если у них одинаковое число вершин
(обозначим его n) и вершины каждого из
них можно занумеровать так числами от
1 до n, что в первом графе две вершины
соединены ребром тогда и только тогда,
когда вершины с такими же номерами во
втором графе соединены.
G1,
G2,
G3
– изоморфны.
Рис.
9, 10, 11 – неизоморфны.
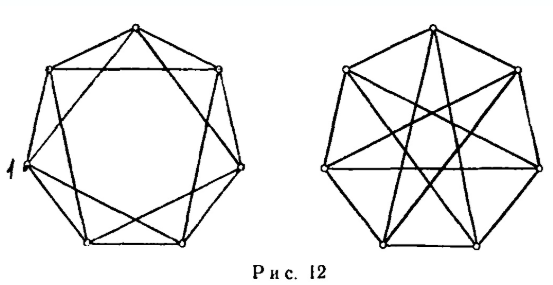
Рис.
12 – изоморфны
Рис.
13 – неизоморфны
G1
G2
G3
|
|
|

Рис.
13
|
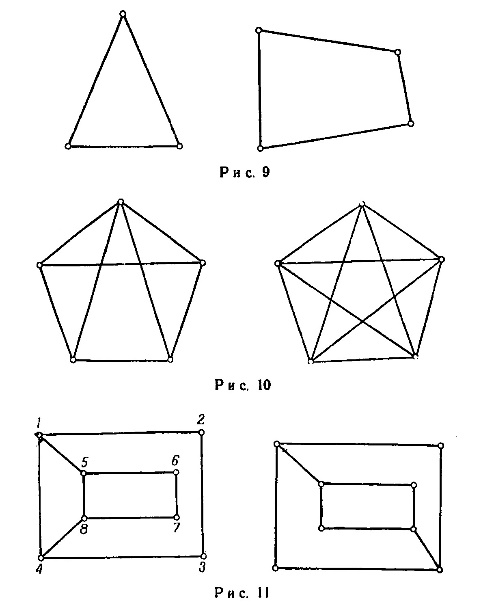
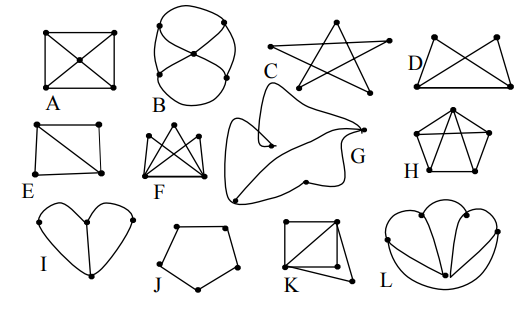
Какие
картинки задают изоморфные графы?
|
|
Степень
вершины
– 1)
для неорграфа количество инцидентных
к вершине ребер, петля учитывается
дважды: 2) для орграфа количество выходящих
ребер, петля учитывается единожды.
Инвариантом
графа
называется некоторая характеристика
графа G,
которая принимает одно и то е значение
для любого графа, изоморфного G.
Существуют
следующие инварианты графов
Количество
вершин n.
Количество
ребер r.
Количество
граней f.
Число
связности k.
Толщина
графа t(G).
Плотность
графа q(G).
Число
независимости
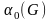
Число
вершинного покрытия
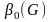
Число
паросочетания
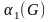 .
.
Число
реберного покрытия
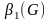 .
.
Число
доминирования
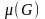
Хроматическое
число
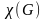
Реберно-хроматическое
число
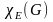
Коцикломатическое
число
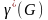
Цикломатическое
число
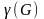
Количество
граней можно найти для плоского связного
графа.
Плоский
граф
– граф, который укладывается на плоскости
так, что никакие два его ребра не
пересекаются нигде, кроме как в инцидентной
им обоим вершине.
Граф
называется связным,
если между любыми его вершинами существует
цепь.
Грань
– область плоскости, ограниченная
ребрами, любые две точки которой могут
быть соединены линией, не пересекающей
ребра графа.
Неограниченная
часть плоскости — тоже грань, так
называемая внешняя
грань.
Любой
граф можно разбить на подграфы, каждый
из которых окажется связным. Минимальное
число таких связных компонент называется
числом связности графа.
Толщина
графа
– минимальное количество его плоских
подграфов, при наложении которых
образуется исходный граф.
 -
формула для поиска толщины графа.
-
формула для поиска толщины графа.
Клика
– полный подграф графа G.
Количество
вершин максимальной клики графа
называется плотностью
графа.
Независимое
множество вершин
-
множество вершин графа, никакие две
вершины которого не инцидентны.
Максимальное
независимое множество вершин
-
независимое
множество вершин,
которое не содержится ни в каком другом
независимом
множестве вершин.
Наибольшее
независимое множество вершин
- независимое
множество вершин максимальной
мощности.
Независимое
множество ребер,
или паросочетание
- множество ребер графа, никакие два
ребра которого не инцидентны.
Мощность
наибольшего независимого
множества вершин называется
числом
независимости
графа (а также неплотностью,
числом
внутренней устойчивости или
числом
вершинной упаковки
графа).
Нахождение
наибольшего
независимого множества
(алгоритм):
1.
В графе выбрать вершину с наименьшей
степенью в качестве элемента исходного
множества.
2.
Удалить выбранную вершину из графа
вместе с ее окрестностью (смежные вершины
и инцидентные им ребра).
Шаги
1—2 повторять до тех пор, пока множество
вершин не станет пустым.
Доминирующее
множество вершин
-
такое множество вершин графа, что каждая
вершина графа либо принадлежит
доминирующему
множеству вершин,
либо инцидентна некоторой вершине из
него.
Число
доминирования графа.
Мощность наименьшего доминирующего
множества называется числом
доминирования
графа.
Для
решения задачи о нахождении числа
доминирования
графа применяется следующий алгоритм:
1.
Дополнить матрицу смежности единицами
по главной диагонали.
2.
Выбрать из матрицы смежности строку с
наибольшим числом единиц и ввести ее в
искомое покрытие.
3.
Вычеркнуть строку из матрицы и столбцы,
покрываемые этой строкой.
Повторять
шаги 2 и 3 до тех пор, пока в матрице
множество столбцов не окажется пустым.
Алгоритм
поиска наибольшего паросочетания:
1.
Выбираем ребро с наименьшей степенью
(число инцидентных вершин) и включаем
в искомое паросочетание. Если таковых
несколько, выбираем то из них, для
которого степень второй граничной
вершины наименьшая.
2.
Удаляем из графа это ребро и ребра,
смежные с ним.
Шаги
1—2 повторять до тех пор, пока множество
ребер не станет пустым.
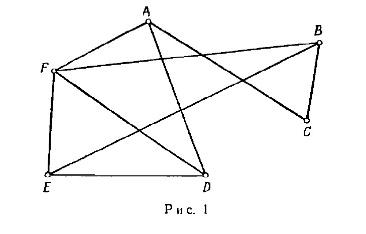
Задача
3.
Найти инварианты графа
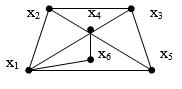
|
1)
Количество вершин n=6.
2)
Количество ребер r=10.
3)
Количество граней f=6
(f1=х1х2х4,
f2=х2х3х4,
f3=х3х4х5,
f4=х1х4х6,
f5=х1х6х4
х5,
f6
- внешняя).
4)
Так как данный граф является плоским
и связным, то число связности k=1.
|
5)
Толщина графа для данного графа
t(G)=1,
так как он является плоским.
В
теории графов толщина графа G — это
наименьшее число плоских подграфов,
на которые можно разложить рёбра
графа G.
6)
Количество
вершин максимальной клики в данном
графе равно 3 и поэтому плотность
графа q(G)=3.
(см. з 4)
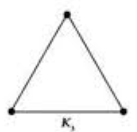
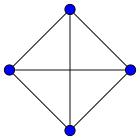
Количество
вершин в графе, которое соединено
всеми возможными ребрами. Т.е. как
правило это или треугольник, или
квадрат с пересечениями, или звезда
и так далее. То есть число вершин в
графе, которые образуют полный граф.
Если нет таких частей в графе, как
снизу, то смотрим, если линия, то
q(G)=2.
Если нет линии даже, то q(G)=1.
|
Пример.
Поиск
максимальной клики
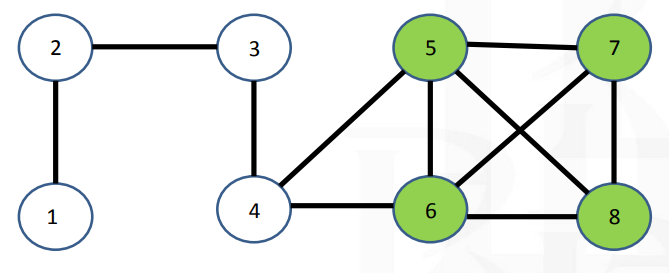
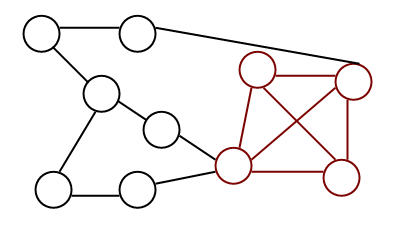
|
7)
Найдем наибольшее независимое
множество вершин графа. Найдем
вершину с наименьшей степенью - х6
((х6)
= 2)
и включим ее в независимое множество.
Удалим из графа саму вершину х6,
смежные ей вершины х1
и
х4
и
инцидентные им ребра х1х2,
х1х4,
х1х5,
х1х6,
х2х4,
х3х4,
х4х5,
х4х6.
В
итоге получим граф вида (рис. 9.6).

Повторяя
шаги алгоритма, далее выбираем х2
с
(х2)
= 1 и
включаем ее в искомое множество, а
после удаления смежных вершин и
инцидентных им ребер оставшуюся
вершину х5.
Таким
образом, мы получили наибольшее
независимое подмножество {х6,
х2,
х5}
и соответственно число независимости
графа
=
3.
|
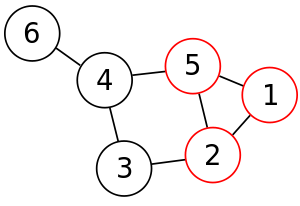
Пример.
Поиск максимального независимого
множества вершин графа
Граф
куба имеет шесть различных наибольших
независимых множества, показанных
красным цветом.

|
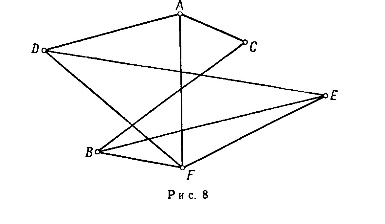
Задача
6. Поиск
независимого множества вершин и
поиск максимального независимого
множества вершин.
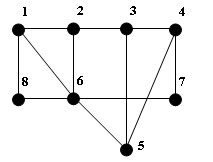
Для
данного графа множества вершин
-
{7,8,2}, {1,3}, {7,8,2,5} - независимые;
-
{1,3,7}, {4,6}, {7,8,2,5} - максимальные.
Следовательно,
в рассмотренном графе больше
одного независимого множества.
Пример
поиска одного из независимых
множеств вершин данного графа.
1)
Берем вершину с наименьшей степенью
– 7 или 8. Возьмем 7 и включим ее в
независимое множество. Вычеркиваем
данную вершину, смежные её ребра
и вершины.
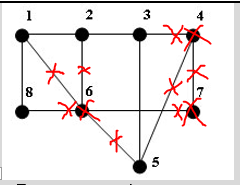
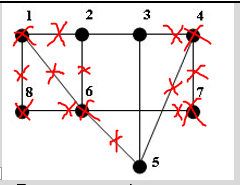
2)
Находим вершину с наименьшей
степенью. Это вершины 5 и 8. Возьмем
8 и включим ее в независимое
множество. Вычеркиваем данную
вершину, смежные её ребра и вершины.
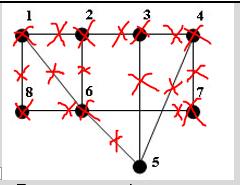
3)
Находим вершину с наименьшей
степенью. Это вершина 2. Включим
ее в независимое множество.
Вычеркиваем данную вершину, смежные
её ребра и вершины.
4)
Осталась вершина 5. Включим ее в
независимое множество.
Таким
образом в максимальном независимом
множестве вершин мы включили 4
вершины {7,8,2,5}.
|
|
8)
Найдем наименьшее вершинное покрытие.
Строим матрицу инцидентности графа
(табл. 9.2).
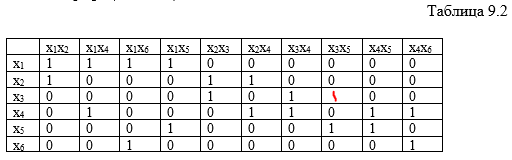
Столбец,
содержащий наименьшее число единиц
(х1х2),
покрывает две строки — х1
и
х2.
Среди них выбираем строку с
максимальным числом единиц и включаем
в искомое покрытие – это строка х1.
Исключаем из матрицы строку х1
и
столбцы, которые она покрывает. В
результате получаем преобразованную
матрицу инцидентности (табл. 7.5) и
повторяем заново шаги алгоритма.
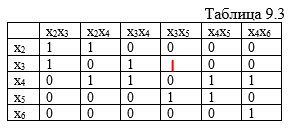
На
этом этапе столбец х2х3
задает
следующую строку искомого покрытия
– х3,
которая покрывает столбцы х2х3,
х3х4,
х3х5.
Переходим к упрощенной матрице
инцидентности (табл. 9.3-9.4).
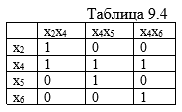
Удалению
из матрицы подлежит строка х4
и
оставшиеся все столбцы.
Из этого можно сформулировать
окончательный вывод: наименьшее
вершинное покрытие составляют
вершины {х1,
х3,
х4}
и число вершинного покрытия 0(G)
= 3.
|
Пример.
Найдем наименьшее вершинное покрытие.
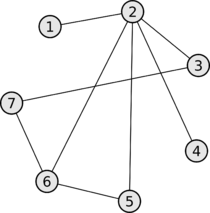
Матрица
инцидентности.
|
1-2
|
2-3
|
2-4
|
2-5
|
2-6
|
3-7
|
5-6
|
6-7
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
3
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
4
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
5
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
6
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
7
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
Находим
столбец с наименьшим числом единиц
(во всех 2).
Берем
столбик (1-2) или любой другой. Он
покрывает строки 1 и 2. Из них выбираем
ту строку, которая содержит наибольшее
число единиц. Выбираем строку (2).
Вычеркиваем строку 2 и все столбцы,
которые она покрывает.
|
1-2
|
2-3
|
2-4
|
2-5
|
2-6
|
3-7
|
5-6
|
6-7
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
2
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
3
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
4
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
5
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
6
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
7
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
|
3-7
|
5-6
|
6-7
|
1
|
0
|
0
|
0
|
3
|
1
|
0
|
0
|
4
|
0
|
0
|
0
|
5
|
0
|
1
|
0
|
6
|
0
|
1
|
1
|
7
|
1
|
0
|
1
|
Повторяем
предыдущие шаги.
Берём
столбец (3-7), строку 7, так как содержит
больше единиц. Вычеркиваем её и
столбцы, которые она покрывает.
|
3-7
|
5-6
|
6-7
|
1
|
0
|
0
|
0
|
3
|
1
|
0
|
0
|
4
|
0
|
0
|
0
|
5
|
0
|
1
|
0
|
6
|
0
|
1
|
1
|
7
|
1
|
0
|
1
|
Далее
берем столбец (5-6) строку ,например,
5.
Наименьшее
вершинное покрытие составляют
вершины {2,7,5} и число вершинного
покрытия 0(G)
= 3.
|
9)
Найдем наибольшее паросочетание.
Алгоритм
поиска наибольшего паросочетания:
1.
Выбираем ребро с наименьшей степенью
(число инцидентных вершин) и включаем
в искомое паросочетание. Если таковых
несколько, выбираем то из них, для
которого степень второй граничной
вершины наименьшая.
2.
Удаляем из графа это ребро и ребра,
смежные с ним.
Шаги
1—2 повторять до тех пор, пока
множество ребер не станет пустым.
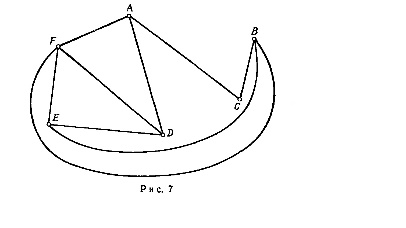
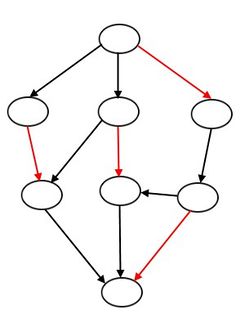
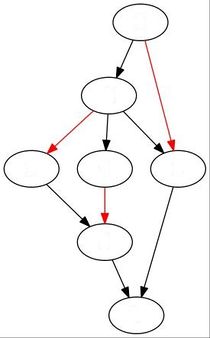
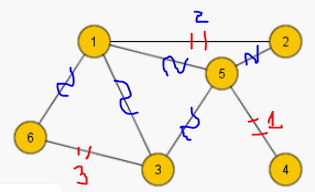
Следуя
вышеописанному алгоритму, первым
можно исключить ребро x2x3
и
смежные ему ребра x1x2,
x2x4,
x3x4,
x3x5.
Исключая следом ребро x4x6,
из графа удаляются ребра x1x4,
x1x6,
x4x5.
Действуя таким образом, в искомое
паросочетание на последнем этапе
включается оставшееся ребро x1x5.
На рис. 9.7а), б), в) изображены
преобразования графа в ходе
последовательного исключения ребер.
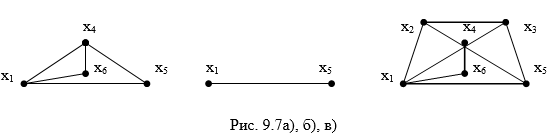
В
итоге получаем, что в искомое покрытие
включаются 3 ребра (на рис. 10.7в ребра,
выделенные жирными линиями) и число
паросочетания 1(G)
= 3.
Согласно
лемме 2 число реберного покрытия
графа 1(G)
= 3.
|
Пример.
Поиск наибольшего паросочетания
(п.9)
 (1,2),(4,5),(3,6)
(1,2),(4,5),(3,6)
|
10)
Найдем наименьшее доминирующее
множество.
Для
решения задачи о нахождении числа
доминирования
графа применяется следующий алгоритм:
1.
Дополнить матрицу смежности единицами
по главной диагонали.
2.
Выбрать из матрицы смежности строку
с наибольшим числом единиц и ввести
ее в искомое покрытие.
3.
Вычеркнуть строку из матрицы и
столбцы, покрываемые этой строкой.
Повторять
шаги 2 и 3 до тех пор, пока в матрице
множество столбцов не окажется
пустым.
Для
этого построим матрицу смежности
и дополним ее единицами по главной
диагонали (табл. 9.6).
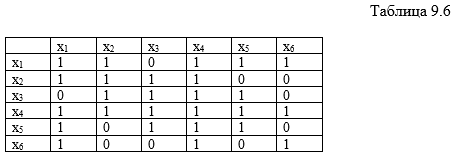
Вводим
в искомое покрытие строку х4,
так как она содержит наибольшее
число единиц, вычеркиваем ее из
матрицы и столбцы, которые она
покрывает. В результате получаем
доминирующее множество вершин {х4}
и число доминирования графа
=
1. Так как строка x4
содержит все единицы, то мы за один
ход вычеркнули всю таблицу. Ниже
приведен пример более сложный.
|
Пример.
Найдем
наименьшее доминирующее множество.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
2
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
3
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
4
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
5
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
6
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
7
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
Находим
строку, которая содержит наибольшее
число единиц. У нас эта строка 2.
Значит включаем вершину 2 в наше
наименьшее доминирующее множество,
вычёркиваем строку 2 и все столбцы,
в которых стояли единицы в данной
строке.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
2
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
3
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
4
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
5
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
6
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
7
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
|
7
|
1
|
0
|
3
|
1
|
4
|
0
|
5
|
0
|
6
|
1
|
7
|
1
|
У
нас осталась таблица, которая
содержит один столбец. Выбираем
строку, которая содержит наибольшее
число единиц. Тут подходят строки
3, 6 и 7. Выбираем любую, например 3. И
включаем в наше искомое наименьшее
доминирующее множество, которое
содержит вершины {2,3}, а число
доминирования равно 2.
|
11)
Найдем коцикломатическое и
цикломатическое числа графа.
Обозначения:
v=6
- число вершин графа,
r=10
- число ребер, равное полусумме
степеней всех вершин графа,
p=1
- число связных компонент графа, в
нашем случае.p=1
так как есть вершина степени 5 и
значит граф связен.
Цикломатическое
число графа вычисляется по формуле
r-v+p=10-6+1=5.
Коцикломатическое
число
– число рёбер в остовном дереве
*(G) = v-p
== 6-1=5
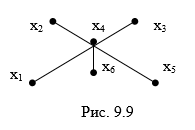
Проверка
коцикломатического числа:
Для
этого построим покрывающее дерево
(рис. 9.9) и подсчитаем число ветвей
и число хорд.
|
Пример.
Найдем коцикломатическое и
цикломатическое числа графа.
Обозначения:
v=7
- число вершин графа,
r=8
- число ребер, равное полусумме
степеней всех вершин графа,
p=1
- число связных компонент графа, в
нашем случае.p=1
так как есть вершина степени 5 и
значит граф связен.
Цикломатическое
число графа вычисляется по формуле
r-v+p=8-7+1=2.
Коцикломатическое
число
– число рёбер в остовном дереве
*(G) = v-p
== 7-1=6
|
|

 .
.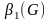 .
.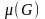
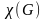
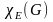
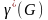
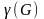
![]() -
формула для поиска толщины графа.
-
формула для поиска толщины графа.



























 (1,2),(4,5),(3,6)
(1,2),(4,5),(3,6)
