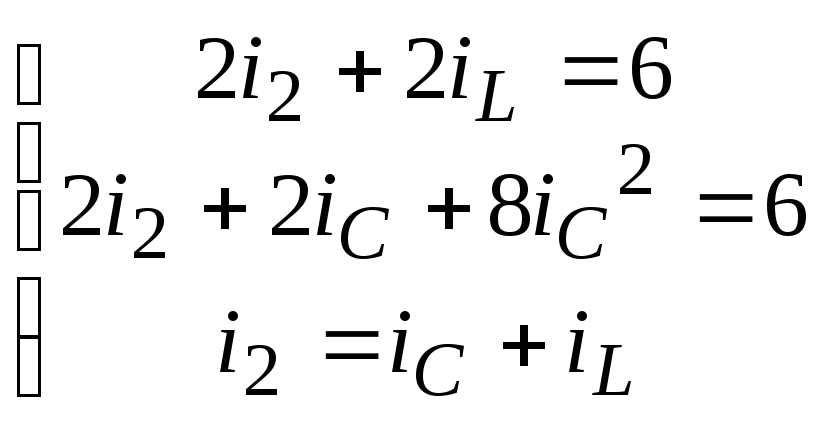Kursovaya_var6
.docВариант №6
Задание на курсовую работу
Электрическая цепь:

Входной сигнал:

Параметры цепи:
U1 = Um = 6;
R2 = 2×103;
R3 = 2×103;
C5 = 0.1×10-6;
L6 = 4;
RH = 2×103;
τИ = 4×10-3;
kУ.И = 18×103;
T = 2τИ
Требуется определить:
-
Анализ линейной цепи классическим методом при коммутации.
-
Анализ линейной цепи операторным методом при апериодическом воздействии.
-
Анализ нелинейной цепи аналитически-численным методом.
Нормирование параметров электрической цепи.
|
Uб = 1 |
|
|
Rб = 103 |
|
|
|
|
|
|
|
|
tб = 10-3 |
|
|
Cб = tб/Rб = 10-6 |
|
|
Lб = tбRб = 1 |
|
|
kб = Rб = 103 |
|
Индексы (*) опустим и все расчеты будем вести с нормированными параметрами.
3.1. Анализ линейной цепи классическим методом при коммутации
3.1.1. Уравнение состояния цепи
Составим уравнение состояния цепи и найдем предначальные условия при t<0:
UС(0-) и iL(0-).
Для этого заменим С на ХХ, а L на КЗ.

UC(0-) = U1 = 6;
![]() ;
;
Для составления уравнений состояния заменим С-элемент источником напряжения UC(t), а L-элемент источником тока iL(t):

В полученной схеме определим iC и UL:
 ,
,

.
Можно представить данное уравнение в матричном виде:

3.1.2. Решение уравнения состояния
Решение уравнения состояния можно представить следующим образом:
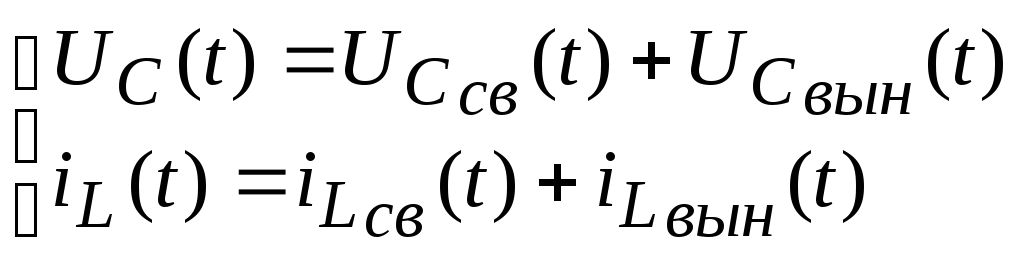
а) kуи = 0
Уравнение состояния в численном виде:

Для определения свободной составляющей составим характеристический полином:

![]() .
.
Тогда свободная составляющая:

Вынужденные колебания находим следующим образом:


Постоянные интегрирования:



Таким образом, переменные состояния цепи:

Выразим напряжение на нагрузке (реакция цепи) через переменные состояния цепи:
![]()

б) kуи = 18
Уравнение состояния в численном виде:

Для определения свободной составляющей составим характеристический полином:

![]()
Тогда свободная составляющая:

Вынужденные колебания находим следующим образом:

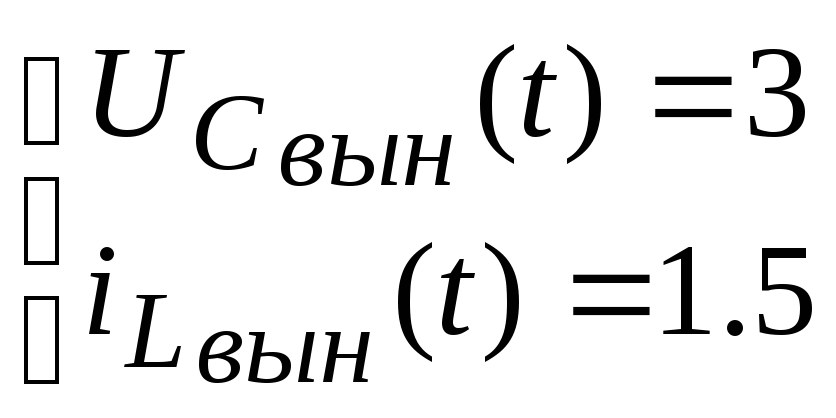
Постоянные интегрирования:



Таким образом, переменные состояния цепи:

Выразим напряжение на нагрузке (реакция цепи) через переменные состояния цепи:
![]()
3.1.3. Определение импульсной и переходной характеристик цепи
Входное воздействие U1(t) = δ1(t).
Начальные условия нулевые: UC(0-) = 0; iL(0-) = 0;
а) kуи = 0
Уравнение состояния в численном виде:

Тогда свободная составляющая:
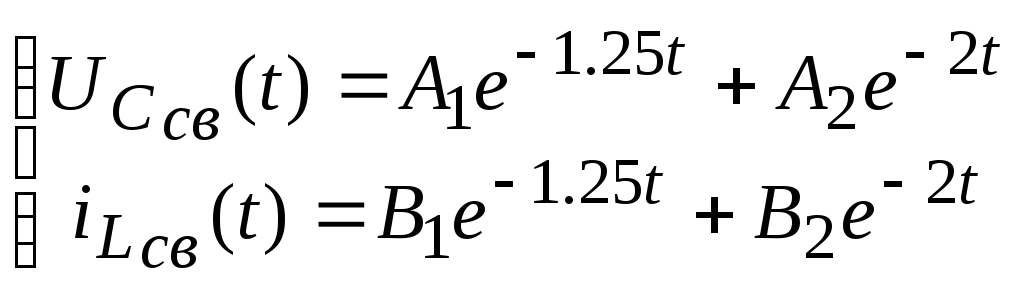
Вынужденные колебания находим следующим образом:
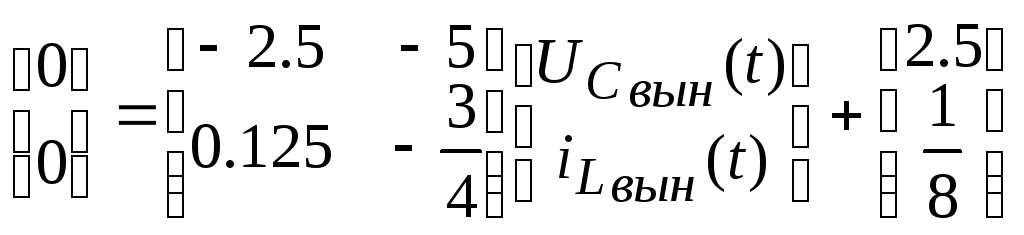

Постоянные интегрирования:



Таким образом, переменные состояния цепи:

Выразим напряжение на нагрузке (реакция цепи) через переменные состояния цепи:
![]()
Переходная характеристика цепи:
![]()

Импульсная характеристика цепи:
![]()

б) kуи = 18
Уравнение состояния в численном виде:

Тогда свободная составляющая:

Вынужденные колебания находим следующим образом:
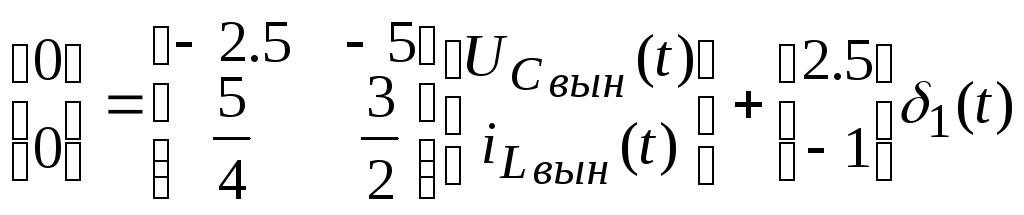

Постоянные интегрирования:


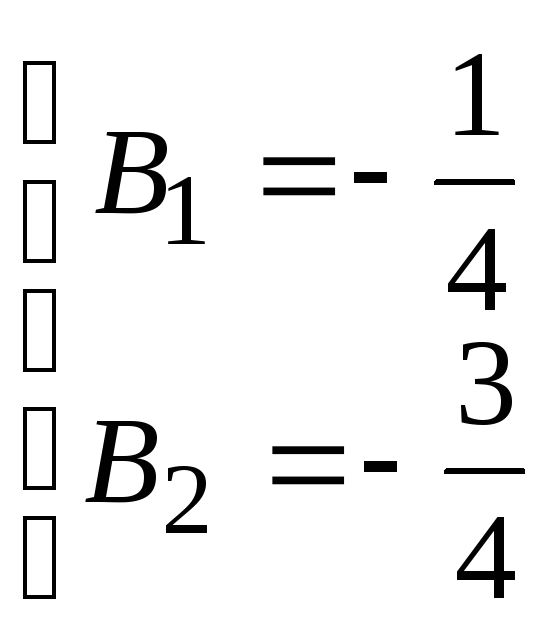
Таким образом, переменные состояния цепи:
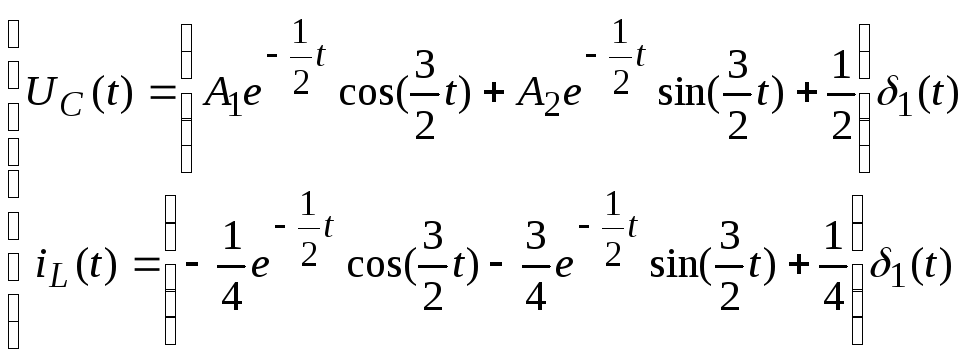
Выразим напряжение на нагрузке (реакция цепи) через переменные состояния цепи:
![]()
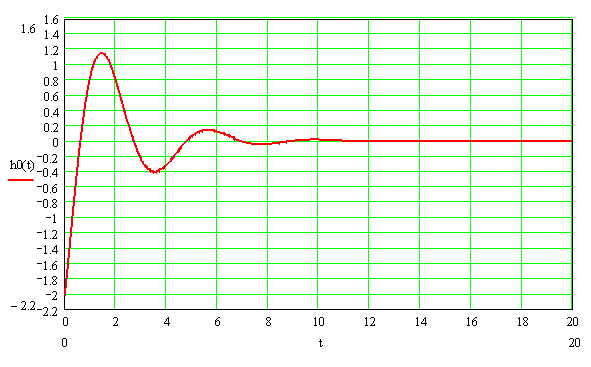
Переходная характеристика цепи:
![]()

Импульсная характеристика цепи:
![]()
.
3.2. Анализ линейной цепи операторным методом при апериодическом воздействии
Начальные условия нулевые: UC(0-) = 0; iL(0-) = 0;
![]() .
.
3.2.1. Составим операторную схему замещения без дополнительных источников.


В полученной схеме определим
![]() :
:

Решая систему уравнений, получим:
![]()
![]()
Функция передачи:
![]()
3.2.2. Определение нулей и полюсов передаточной функции.
a). kуи = 0:
![]()
Полюсы:
![]()
Нули:
![]()

б). kуи = 18:
![]()
Полюсы:
![]()
Нули:
![]()

3.2.3. Определение изображения по Лапласу одиночного импульса

Во временной области сигнал можно представить в виде:
![]() .
.
Используя теорему смещения в p-области, найдем изображение по Лапласу:
![]()
a). kуи = 0:
![]() ,
,
![]() ,
,
![]()
![]()
б). kуи = 18:
![]() ,
,
![]()
![]()
![]()

3.3. Анализ нелинейной цепи аналитически-численным методом
Нормирование параметров электрической цепи.
![]() ,
следовательно,
,
следовательно,

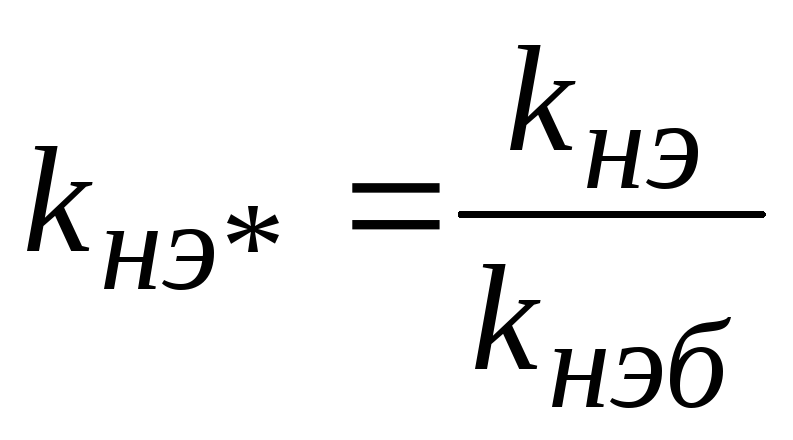 .
.
Таким образом,
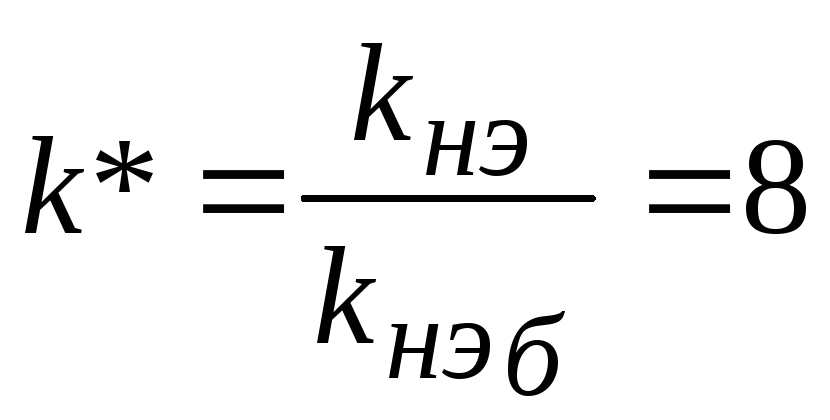
Индекс (*) опустим и все расчеты будем вести с нормированными параметрами
3.3.1. Уравнение состояния

Составим уравнение состояния:
 ,
,
![]()
Решая уравнение, получим:
![]()
Определим знак перед корнем. Для этого
будем анализировать цепь при
![]() .
.
|
Определение знака перед корнем:
При
Тогда UL=0. Найдем iL:
Решая систему уравнений, получим:
Подставив
|
![]()
![]()
Будем искать решение уравнения состояния в виде отрезков ряда Тейлора:
![]()
Тогда:

Произведем замену:

Тогда:
 .
.
Возведем полином в степень 0.5:
![]()
где:

Преобразование Лапласа:
![]()
Произведем замену:

тогда:
![]()
Выразим
![]() :
:

где:

Тогда искомые коэффициенты Ri можно найти по формуле:
 .
.
Оценка точности решения может быть определена по значению остаточного члена ряда Тейлора. Если среди коэффициентов |Ri| существует максимум |Rk|, то локальная погрешность может быть оценена по формуле:

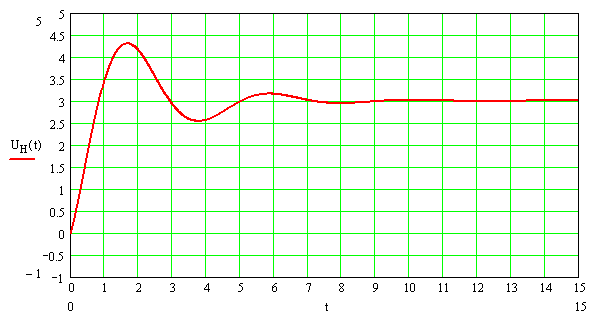
По уравнению связи найдем напряжение на нагрузке:
UH = RH∙iL(t)
|
h |
t |
R0 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
R7 |
|
|
|
0,1 |
0,001 |
0 |
1,174306 |
-1,09288 |
0,874891 |
-0,85361 |
0,814815 |
-0,77258 |
0,733311 |
0,112109 |
2,95E-13 |
|
0,1 |
0,1 |
0,112109 |
1,070039 |
-0,99453 |
0,779542 |
-0,76119 |
0,726078 |
-0,68723 |
0,651006 |
0,214267 |
2,68E-13 |
|
0,1 |
0,2 |
0,214267 |
0,97515 |
-0,90519 |
0,693016 |
-0,67737 |
0,645738 |
-0,61011 |
0,576813 |
0,307368 |
2,45E-13 |
|
0,1 |
0,3 |
0,307368 |
0,888779 |
-0,82401 |
0,614479 |
-0,60135 |
0,572984 |
-0,54043 |
0,509926 |
0,392226 |
2,23E-13 |
|
0,1 |
0,4 |
0,392226 |
0,81015 |
-0,75025 |
0,543179 |
-0,53237 |
0,507084 |
-0,47744 |
0,449618 |
0,469578 |
2,03E-13 |
|
0,1 |
0,5 |
0,469578 |
0,738557 |
-0,68319 |
0,478436 |
-0,46976 |
0,447375 |
-0,42051 |
0,395233 |
0,540096 |
1,85E-13 |
|
0,1 |
0,6 |
0,540096 |
0,67336 |
-0,62223 |
0,419633 |
-0,41294 |
0,393263 |
-0,36902 |
0,346178 |
0,604389 |
1,69E-13 |
|
0,1 |
0,7 |
0,604389 |
0,613978 |
-0,56679 |
0,366214 |
-0,36134 |
0,344208 |
-0,32244 |
0,301922 |
0,663012 |
1,54E-13 |
|
0,1 |
0,8 |
0,663012 |
0,559885 |
-0,51637 |
0,317675 |
-0,31449 |
0,299726 |
-0,28031 |
0,261984 |
0,716471 |
1,66E-13 |
|
0,1 |
0,9 |
0,716471 |
0,510603 |
-0,4705 |
0,273561 |
-0,27192 |
0,259378 |
-0,24217 |
0,225932 |
0,765223 |
1,8E-13 |
|
0,1 |
1 |
0,765223 |
0,465698 |
-0,42877 |
0,233459 |
-0,23325 |
0,222769 |
-0,20763 |
0,193378 |
0,809687 |
1,92E-13 |
|
0,1 |
1,1 |
0,809687 |
0,424776 |
-0,39079 |
0,196996 |
-0,1981 |
0,189543 |
-0,17636 |
0,163972 |
0,850242 |
2,03E-13 |
|
0,1 |
1,2 |
0,850242 |
0,387479 |
-0,35621 |
0,163835 |
-0,16615 |
0,159379 |
-0,14803 |
0,137401 |
0,887236 |
2,13E-13 |
|
0,1 |
1,3 |
0,887236 |
0,353482 |
-0,32474 |
0,133671 |
-0,13709 |
0,131986 |
-0,12235 |
0,11338 |
0,920982 |
2,23E-13 |
|
0,1 |
1,4 |
0,920982 |
0,32249 |
-0,29608 |
0,106226 |
-0,11067 |
0,107103 |
-0,09907 |
0,091658 |
0,951768 |
2,31E-13 |
|
0,1 |
1,5 |
0,951768 |
0,294234 |
-0,26997 |
0,081251 |
-0,08663 |
0,084493 |
-0,07795 |
0,072006 |
0,979855 |
2,39E-13 |
|
0,1 |
1,6 |
0,979855 |
0,26847 |
-0,2462 |
0,058518 |
-0,06476 |
0,063944 |
-0,05879 |
0,054219 |
1,00548 |
2,46E-13 |
|
0,1 |
1,7 |
1,00548 |
0,244977 |
-0,22454 |
0,037823 |
-0,04486 |
0,045261 |
-0,04141 |
0,038113 |
1,028861 |
2,52E-13 |
|
0,1 |
1,8 |
1,028861 |
0,223552 |
-0,2048 |
0,01898 |
-0,02674 |
0,028272 |
-0,02562 |
0,023525 |
1,050195 |
2,58E-13 |
|
0,1 |
1,9 |
1,050195 |
0,204011 |
-0,18682 |
0,001819 |
-0,01024 |
0,012819 |
-0,01128 |
0,010304 |
1,069663 |
2,63E-13 |
|
0,1 |
2 |
1,069663 |
0,186188 |
-0,17043 |
-0,01381 |
0,004776 |
-0,00124 |
0,00174 |
-0,00168 |
1,087427 |
2,68E-13 |
|
0,1 |
2,1 |
1,087427 |
0,169931 |
-0,15549 |
-0,02805 |
0,018456 |
-0,01404 |
0,013575 |
-0,01255 |
1,103638 |
2,73E-13 |
|
0,1 |
2,2 |
1,103638 |
0,1551 |
-0,14187 |
-0,04103 |
0,030917 |
-0,02568 |
0,024334 |
-0,02242 |
1,118432 |
2,77E-13 |
|
0,1 |
2,3 |
1,118432 |
0,141571 |
-0,12945 |
-0,05285 |
0,042269 |
-0,03628 |
0,034117 |
-0,03137 |
1,131933 |
2,81E-13 |
|
0,1 |
2,4 |
1,131933 |
0,129227 |
-0,11813 |
-0,06362 |
0,052614 |
-0,04594 |
0,043014 |
-0,0395 |
1,144255 |
2,84E-13 |
|
0,1 |
2,5 |
1,144255 |
0,117965 |
-0,1078 |
-0,07344 |
0,06204 |
-0,05473 |
0,051109 |
-0,04688 |
1,155501 |
2,87E-13 |
|
0,1 |
2,6 |
1,155501 |
0,10769 |
-0,09839 |
-0,0824 |
0,070632 |
-0,06274 |
0,058476 |
-0,05359 |
1,165764 |
2,9E-13 |
|
0,1 |
2,7 |
1,165764 |
0,098314 |
-0,0898 |
-0,09056 |
0,078464 |
-0,07004 |
0,06518 |
-0,05969 |
1,175132 |
2,92E-13 |
|
0,1 |
2,8 |
1,175132 |
0,089758 |
-0,08197 |
-0,098 |
0,085605 |
-0,07669 |
0,071284 |
-0,06523 |
1,183682 |
2,95E-13 |
|
0,1 |
2,9 |
1,183682 |
0,081951 |
-0,07482 |
-0,10479 |
0,092114 |
-0,08275 |
0,076843 |
-0,07027 |
1,191486 |
2,97E-13 |
|
0,1 |
3 |
1,191486 |
0,074826 |
-0,06831 |
-0,11098 |
0,09805 |
-0,08827 |
0,081905 |
-0,07486 |
1,198609 |
2,99E-13 |
|
0,1 |
3,1 |
1,198609 |
0,068324 |
-0,06236 |
-0,11662 |
0,103464 |
-0,09331 |
0,086516 |
-0,07903 |
1,20511 |
3,01E-13 |
|
0,1 |
3,2 |
1,20511 |
0,062391 |
-0,05694 |
-0,12177 |
0,1084 |
-0,0979 |
0,090718 |
-0,08283 |
1,211045 |
3,02E-13 |
|
0,1 |
3,3 |
1,211045 |
0,056975 |
-0,05199 |
-0,12647 |
0,112903 |
-0,10208 |
0,094546 |
-0,08629 |
1,216462 |
3,04E-13 |
|
0,1 |
3,4 |
1,216462 |
0,052033 |
-0,04747 |
-0,13075 |
0,11701 |
-0,1059 |
0,098035 |
-0,08944 |
1,221406 |
3,05E-13 |
|
0,1 |
3,5 |
1,221406 |
0,047522 |
-0,04335 |
-0,13466 |
0,120757 |
-0,10938 |
0,101215 |
-0,09231 |
1,22592 |
3,06E-13 |
|
0,1 |
3,6 |
1,22592 |
0,043405 |
-0,03959 |
-0,13823 |
0,124175 |
-0,11255 |
0,104114 |
-0,09492 |
1,23004 |
3,08E-13 |
|
0,1 |
3,7 |
1,23004 |
0,039647 |
-0,03616 |
-0,14148 |
0,127293 |
-0,11545 |
0,106757 |
-0,0973 |
1,233801 |
3,09E-13 |
|
0,1 |
3,8 |
1,233801 |
0,036217 |
-0,03303 |
-0,14445 |
0,130138 |
-0,11809 |
0,109167 |
-0,09947 |
1,237234 |
3,1E-13 |
|
0,1 |
3,9 |
1,237234 |
0,033086 |
-0,03017 |
-0,14716 |
0,132734 |
-0,1205 |
0,111365 |
-0,10145 |
1,240367 |
3,1E-13 |
|
0,1 |
4 |
1,240367 |
0,030229 |
-0,02756 |
-0,14963 |
0,135102 |
-0,12269 |
0,113369 |
-0,10325 |
1,243228 |
3,11E-13 |
|
0,1 |
4,1 |
1,243228 |
0,02762 |
-0,02518 |
-0,15188 |
0,137263 |
-0,1247 |
0,115197 |
-0,10489 |
1,24584 |
3,12E-13 |
|
0,1 |
4,2 |
1,24584 |
0,02524 |
-0,02301 |
-0,15394 |
0,139236 |
-0,12653 |
0,116864 |
-0,10639 |
1,248223 |
3,13E-13 |
|
0,1 |
4,3 |
1,248223 |
0,023066 |
-0,02103 |
-0,15582 |
0,141035 |
-0,1282 |
0,118385 |
-0,10776 |
1,250399 |
3,13E-13 |
|
0,1 |
4,4 |
1,250399 |
0,021082 |
-0,01922 |
-0,15754 |
0,142678 |
-0,12972 |
0,119772 |
-0,109 |
1,252386 |
3,14E-13 |
|
0,1 |
4,5 |
1,252386 |
0,019272 |
-0,01757 |
-0,1591 |
0,144177 |
-0,13111 |
0,121038 |
-0,11014 |
1,254199 |
3,14E-13 |
|
0,1 |
4,6 |
1,254199 |
0,017619 |
-0,01606 |
-0,16053 |
0,145545 |
-0,13238 |
0,122193 |
-0,11117 |
1,255855 |
3,15E-13 |
|
0,1 |
4,7 |
1,255855 |
0,01611 |
-0,01468 |
-0,16183 |
0,146793 |
-0,13354 |
0,123246 |
-0,11212 |
1,257366 |
3,15E-13 |
|
0,1 |
4,8 |
1,257366 |
0,014732 |
-0,01343 |
-0,16302 |
0,147933 |
-0,13459 |
0,124208 |
-0,11298 |
1,258745 |
3,15E-13 |
|
0,1 |
4,9 |
1,258745 |
0,013475 |
-0,01228 |
-0,16411 |
0,148973 |
-0,13556 |
0,125085 |
-0,11377 |
1,260005 |
3,16E-13 |
|
0,1 |
5 |
1,260005 |
0,012327 |
-0,01123 |
-0,1651 |
0,149922 |
-0,13644 |
0,125885 |
-0,11448 |
1,261154 |
3,16E-13 |
|
0,1 |
5,1 |
1,261154 |
0,011279 |
-0,01028 |
-0,166 |
0,150788 |
-0,13724 |
0,126616 |
-0,11514 |
1,262204 |
3,16E-13 |
|
0,1 |
5,2 |
1,262204 |
0,010323 |
-0,00941 |
-0,16683 |
0,151579 |
-0,13797 |
0,127283 |
-0,11574 |
1,263162 |
3,17E-13 |
|
0,1 |
5,3 |
1,263162 |
0,00945 |
-0,00861 |
-0,16758 |
0,152301 |
-0,13864 |
0,127891 |
-0,11628 |
1,264037 |
3,17E-13 |
|
0,1 |
5,4 |
1,264037 |
0,008653 |
-0,00789 |
-0,16827 |
0,15296 |
-0,13925 |
0,128446 |
-0,11678 |
1,264835 |
3,17E-13 |
|
0,1 |
5,5 |
1,264835 |
0,007925 |
-0,00722 |
-0,1689 |
0,153561 |
-0,13981 |
0,128953 |
-0,11723 |
1,265564 |
3,17E-13 |
|
0,1 |
5,6 |
1,265564 |
0,007261 |
-0,00662 |
-0,16947 |
0,15411 |
-0,14032 |
0,129416 |
-0,11765 |
1,266229 |
3,18E-13 |
|
0,1 |
5,7 |
1,266229 |
0,006655 |
-0,00606 |
-0,16999 |
0,154611 |
-0,14078 |
0,129838 |
-0,11802 |
1,266837 |
3,18E-13 |
|
0,1 |
5,8 |
1,266837 |
0,006101 |
-0,00556 |
-0,17047 |
0,155069 |
-0,1412 |
0,130223 |
-0,11837 |
1,267391 |
3,18E-13 |
|
0,1 |
5,9 |
1,267391 |
0,005596 |
-0,0051 |
-0,17091 |
0,155486 |
-0,14159 |
0,130575 |
-0,11868 |
1,267898 |
3,18E-13 |
|
0,1 |
6 |
1,267898 |
0,005135 |
-0,00468 |
-0,17131 |
0,155868 |
-0,14194 |
0,130896 |
-0,11897 |
1,26836 |
3,18E-13 |
|
0,1 |
6,1 |
1,26836 |
0,004713 |
-0,00429 |
-0,17167 |
0,156215 |
-0,14227 |
0,131189 |
-0,11923 |
1,268782 |
3,18E-13 |
|
0,1 |
6,2 |
1,268782 |
0,004329 |
-0,00394 |
-0,172 |
0,156533 |
-0,14256 |
0,131456 |
-0,11947 |
1,269167 |
3,18E-13 |
|
0,1 |
6,3 |
1,269167 |
0,003978 |
-0,00362 |
-0,1723 |
0,156823 |
-0,14283 |
0,1317 |
-0,11969 |
1,269518 |
3,18E-13 |
|
0,1 |
6,4 |
1,269518 |
0,003658 |
-0,00333 |
-0,17258 |
0,157088 |
-0,14308 |
0,131923 |
-0,11989 |
1,269839 |
3,18E-13 |
|
0,1 |
6,5 |
1,269839 |
0,003365 |
-0,00307 |
-0,17283 |
0,157329 |
-0,1433 |
0,132126 |
-0,12007 |
1,270132 |
3,19E-13 |
|
0,1 |
6,6 |
1,270132 |
0,003098 |
-0,00282 |
-0,17306 |
0,15755 |
-0,1435 |
0,132312 |
-0,12024 |
1,2704 |
3,19E-13 |
|
0,1 |
6,7 |
1,2704 |
0,002854 |
-0,0026 |
-0,17327 |
0,157751 |
-0,14369 |
0,132482 |
-0,12039 |
1,270644 |
3,19E-13 |
|
0,1 |
6,8 |
1,270644 |
0,002632 |
-0,0024 |
-0,17346 |
0,157935 |
-0,14386 |
0,132636 |
-0,12053 |
1,270867 |
3,19E-13 |
|
0,1 |
6,9 |
1,270867 |
0,002429 |
-0,00221 |
-0,17364 |
0,158103 |
-0,14402 |
0,132777 |
-0,12065 |
1,271071 |
3,19E-13 |
|
0,1 |
7 |
1,271071 |
0,002243 |
-0,00204 |
-0,1738 |
0,158256 |
-0,14416 |
0,132906 |
-0,12077 |
1,271256 |
3,19E-13 |
|
0,1 |
7,1 |
1,271256 |
0,002074 |
-0,00189 |
-0,17394 |
0,158396 |
-0,14429 |
0,133024 |
-0,12087 |
1,271426 |
3,19E-13 |
|
0,1 |
7,2 |
1,271426 |
0,00192 |
-0,00175 |
-0,17408 |
0,158523 |
-0,1444 |
0,133131 |
-0,12097 |
1,271581 |
3,19E-13 |
|
0,1 |
7,3 |
1,271581 |
0,001778 |
-0,00162 |
-0,1742 |
0,15864 |
-0,14451 |
0,13323 |
-0,12106 |
1,271722 |
3,19E-13 |
|
0,1 |
7,4 |
1,271722 |
0,00165 |
-0,0015 |
-0,17431 |
0,158746 |
-0,14461 |
0,133319 |
-0,12114 |
1,271851 |
3,19E-13 |
|
0,1 |
7,5 |
1,271851 |
0,001532 |
-0,0014 |
-0,17441 |
0,158843 |
-0,1447 |
0,133401 |
-0,12121 |
1,271969 |
3,19E-13 |
|
0,1 |
7,6 |
1,271969 |
0,001425 |
-0,0013 |
-0,1745 |
0,158932 |
-0,14478 |
0,133475 |
-0,12128 |
1,272077 |
3,19E-13 |
|
0,1 |
7,7 |
1,272077 |
0,001327 |
-0,00121 |
-0,17459 |
0,159013 |
-0,14486 |
0,133544 |
-0,12134 |
1,272175 |
3,19E-13 |
|
0,1 |
7,8 |
1,272175 |
0,001237 |
-0,00113 |
-0,17467 |
0,159087 |
-0,14493 |
0,133606 |
-0,12139 |
1,272264 |
3,19E-13 |
|
0,1 |
7,9 |
1,272264 |
0,001156 |
-0,00105 |
-0,17474 |
0,159154 |
-0,14499 |
0,133662 |
-0,12144 |
1,272346 |
3,19E-13 |
|
0,1 |
8 |
1,272346 |
0,001081 |
-0,00098 |
-0,1748 |
0,159216 |
-0,14505 |
0,133714 |
-0,12149 |
1,272421 |
3,19E-13 |
|
0,1 |
8,1 |
1,272421 |
0,001013 |
-0,00092 |
-0,17486 |
0,159272 |
-0,1451 |
0,133762 |
-0,12153 |
1,272489 |
3,19E-13 |
|
0,1 |
8,2 |
1,272489 |
0,000951 |
-0,00087 |
-0,17491 |
0,159323 |
-0,14515 |
0,133805 |
-0,12157 |
1,272551 |
3,19E-13 |
|
0,1 |
8,3 |
1,272551 |
0,000894 |
-0,00081 |
-0,17496 |
0,15937 |
-0,14519 |
0,133844 |
-0,12161 |
1,272608 |
3,19E-13 |
|
0,1 |
8,4 |
1,272608 |
0,000842 |
-0,00077 |
-0,17501 |
0,159413 |
-0,14523 |
0,13388 |
-0,12164 |
1,27266 |
3,19E-13 |
|
0,1 |
8,5 |
1,27266 |
0,000795 |
-0,00072 |
-0,17505 |
0,159452 |
-0,14526 |
0,133913 |
-0,12167 |
1,272707 |
3,19E-13 |
|
0,1 |
8,6 |
1,272707 |
0,000752 |
-0,00069 |
-0,17509 |
0,159488 |
-0,1453 |
0,133943 |
-0,1217 |
1,272751 |
3,19E-13 |
|
0,1 |
8,7 |
1,272751 |
0,000713 |
-0,00065 |
-0,17512 |
0,15952 |
-0,14533 |
0,13397 |
-0,12172 |
1,27279 |
3,19E-13 |
|
0,1 |
8,8 |
1,27279 |
0,000677 |
-0,00062 |
-0,17515 |
0,15955 |
-0,14536 |
0,133995 |
-0,12174 |
1,272826 |
3,19E-13 |
|
0,1 |
8,9 |
1,272826 |
0,000644 |
-0,00059 |
-0,17518 |
0,159577 |
-0,14538 |
0,134018 |
-0,12176 |
1,272859 |
3,19E-13 |
|
0,1 |
9 |
1,272859 |
0,000614 |
-0,00056 |
-0,1752 |
0,159602 |
-0,1454 |
0,134039 |
-0,12178 |
1,272889 |
3,19E-13 |
|
0,1 |
9,1 |
1,272889 |
0,000586 |
-0,00053 |
-0,17523 |
0,159624 |
-0,14542 |
0,134058 |
-0,1218 |
1,272917 |
3,19E-13 |
|
0,1 |
9,2 |
1,272917 |
0,000561 |
-0,00051 |
-0,17525 |
0,159645 |
-0,14544 |
0,134075 |
-0,12181 |
1,272942 |
3,19E-13 |
|
0,1 |
9,3 |
1,272942 |
0,000539 |
-0,00049 |
-0,17527 |
0,159664 |
-0,14546 |
0,134091 |
-0,12183 |
1,272964 |
3,19E-13 |
|
0,1 |
9,4 |
1,272964 |
0,000518 |
-0,00047 |
-0,17529 |
0,159681 |
-0,14548 |
0,134106 |
-0,12184 |
1,272985 |
3,19E-13 |
|
0,1 |
9,5 |
1,272985 |
0,000499 |
-0,00045 |
-0,1753 |
0,159697 |
-0,14549 |
0,134119 |
-0,12185 |
1,273004 |
3,19E-13 |
|
0,1 |
9,6 |
1,273004 |
0,000481 |
-0,00044 |
-0,17532 |
0,159711 |
-0,1455 |
0,134131 |
-0,12186 |
1,273022 |
3,19E-13 |
|
0,1 |
9,7 |
1,273022 |
0,000466 |
-0,00042 |
-0,17533 |
0,159724 |
-0,14552 |
0,134142 |
-0,12187 |
1,273038 |
3,19E-13 |
|
0,1 |
9,8 |
1,273038 |
0,000451 |
-0,00041 |
-0,17534 |
0,159736 |
-0,14553 |
0,134152 |
-0,12188 |
1,273052 |
3,19E-13 |