
Лабораторные работы / ЛР3
.pdf
Отчет по лабораторной работе № 3 на тему: «Решение СЛАУ итерационными методами»
по дисциплине «Вычислительные методы»
Постановка задачи.
Дана система уравнений. Найдите решение этой системы Ax=b А) методом Якоби; Б) методом Зейделя;
В) методом релаксации (SOR), подобрав наилучший (по возможности) параметр; Г) методом сопряженных градиентов (CG).
Сравните быстроту работы методов (по количеству итераций). Задачу следует решить для систем порядка (m) 5, 10 и 100.
1. Матрица A задается с помощью функции:
matrA(m) := |
for i 1 .. m |
|
|
||
|
|
||||
|
for j 1 .. m |
|
|
||
|
A |
← |
cos(i + j) |
+ 110 e |
− (i−j )2 |
|
0.1 110 |
|
|||
|
i ,j |
|
|
|
|
|
A |
|
|
|
|
Для m=5:
109.9621685 |
40.3767392 |
1.9552981 |
0.0393625 |
0.0873006 |
|
|
|
40.3767392 |
109.9405779 |
40.492526 |
2.1020085 |
0.0821116 |
|
|
|
|||||
A = |
1.9552981 |
40.492526 |
110.0872882 40.5352751 |
2.001493 |
|
|
|
0.0393625 |
2.1020085 |
40.5352751 |
109.9867727 |
40.3839085 |
|
|
0.0873006 |
0.0821116 |
2.001493 |
40.3839085 |
|
|
|
109.9237208 |
|||||
Вектор правых частей b задается с помощью функции:
vectb (m) := for i 1.. m
bi ← 0.1 i3 + 110
b
Для m=5:
110.1
110.8 b = 112.7
116.4122.5
2. Матрица B задается с помощью функции:
matrB(A ,m) := |
for i 1..m |
|
|
||||||
|
|
||||||||
|
for j 1..m |
|
|
||||||
|
|
|
|
Bi,j |
← 0 if i |
|
j |
||
|
|
|
|
||||||
|
|||||||||
|
|||||||||
|
|
|
|
B |
← |
−Ai,j |
|
if i ≠ j |
|
|
|
|
|
|
|
|
|||
|
|
|
|
i,j |
|
Ai,i |
|
|
|
|
|
|
|
|
|
|
|
||
|
B |
|
|
|
|
|
|||
Для m=5:
|
0 |
|
|
|
|
−0.3671875 |
|
− 4 |
− 4 |
|
|
|
|
|
|
|
−0.0177816 −3.5796447× 10 |
−7.9391474× 10 |
|
||||
|
−0.3672597 |
|
|
|
|
−0.3683128 |
|
− 4 |
|||
|
|
0 |
−0.0191195 |
−7.4687298× 10 |
|
||||||
B = |
−0.0177613 |
|
|
−0.367822 |
0 |
−0.3682103 |
−0.018181 |
|
|||
|
−3.578844× 10− 4 |
|
−0.0191115 |
−0.3685468 |
0 |
−0.3671706 |
|
||||
|
|
|
|||||||||
|
−7.9419243× 10− 4 |
−7.4698752× 10− 4 |
−0.018208 |
−0.3673812 |
0 |
|
|||||
|
|
||||||||||
Вектор c задается с помощью функции: |
|
|
|
||||||||
vectc (A ,b ,m) := |
|
for |
i 1..m |
|
|
|
|
||||
|
|
|
|
|
|||||||
|
|
|
ci |
← |
|
bi |
|
|
|
|
|
|
|
|
|
Ai,i |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
c |
|
|
|
|
|
|
|
|
Для m=5: |
|
|
|
|
|
|
|
|
|||
|
1.0012534 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
1.0078172 |
|
|
|
|
|
|
|
|
||
c=
3.Проверка условия сходимости для m=5 для нормы ||·||∞1.02373311.05830911.1144091
normi(B) = 0.7719746
Полученное значение меньше 1, следовательно условие сходимости выполняется.
2
4. Программы, реализующие итерационные методы. Обозначения:
n – число неизвестных, m – число итераций,
x0 – начальное приближение,
A, B – матрицы из пунктов 1-2, рассчитанные по функциям для соответствующих значений n,
b, c – вектора из пунктов 1-2, рассчитанные по функциям для соответствующих значений n.
Программа, реализующая метод Якоби:
yukobi(m,n ,x0,A ,b ,B,c) := |
x ← x0 |
|
|
|
|
|||||||||
|
k ← 0 |
|
|
|
|
|
|
|
|
|
||||
|
g0 ← 0 |
|
|
|
|
|||||||||
|
r0 ← b − A x |
|
|
|
|
|||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
→ |
|
|
|||||||
r0 ← max( |
|
r0 |
|
|
) |
|
|
|||||||
|
|
|
|
|||||||||||
|
while k < m |
|
|
|
|
|||||||||
|
|
|
|
|
||||||||||
|
|
|
|
y ← x |
|
|
|
|
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
for i 1..n |
|
|
||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
(Bi,j yj)+ ci |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
xi ← ∑ |
||||||||
|
|
|
|
|
|
|
|
j = 1 |
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
rez |
|
|
← x |
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
i,k+1 |
|
i |
||||||
|
|
|
k ← k + 1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
rk ← b − A x |
|
|||||||||
|
|
|
|
|
|
→ |
||||||||
|
|
|
|
|
|
|||||||||
|
|
|
rk ← max( |
|
rk |
) |
||||||||
|
|
|
|
|
||||||||||
|
|
|
|
g |
k |
← k |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
stack(augment(g0,r0,x0T),augment(g ,r,rezT)) |
|||||||||||||
3

Программа, реализующая метод Зейделя:
zeid(m,n ,x0,A ,b ,B,c) := x ← x0 |
|
||||
k ← 0 |
|
||||
g0 ← 0 |
|
||||
r0 |
← b − A x |
|
|||
|
→ |
||||
r0 |
← max( |
|
r0 |
|
) |
|
|
||||
while k < m for i 1..n
n
xi ← ∑ (Bi,j xj)+ ci j = 1
rezi,k+1 ← xi k ← k + 1
rk ← b − A x
→ rk ← max( rk )
gk ← k
stack(augment(g0,r0,x0T),augment(g ,r,rezT))
Программа, реализующая метод релаксации:
rel(m,n ,x0,A ,b ,B,c,w) := x ← x0 |
|
|||||
k ← 0 |
|
|||||
g0 ← 0 |
|
|||||
r0 ← b − A x |
|
|||||
→ |
|
|||||
r0 ← max( |
r0 |
) |
|
|
||
while k < m |
|
|||||
for i 1..n |
|
|||||
|
|
|
|
n |
(Bi,j xj)+ w ci + (1 − w) xi |
|
|
|
|
||||
|
xi ← w ∑ |
|||||
|
|
|
|
j = 1 |
|
|
|
rezi,k+1 ← xi |
|||||
k ← k + 1 |
|
|||||
rk ← b − A x |
|
|||||
|
→ |
|
||||
rk ← max( |
rk |
) |
|
|||
gk ← k
stack(augment(g0,r0,x0T),augment(g ,r,rezT))
4

5.Значение параметра ω для метода релаксации, при котором норма невязки убывает быстрее всего:
ω =1,1
6.Программа, реализующая метод сопряженных градиентов:
grad(m,x0,A ,b) := r0 ← b − A x0 |
|
|
|||||||||
result1,3 ← x0T |
|
|
|||||||||
p0 ← r0 |
|
|
|||||||||
alf ← |
r0 r0 |
|
|
|
|
|
|
|
|
||
A r0 r0 |
|
|
|||||||||
|
|
|
|
||||||||
x2 ← x0 + alf p0 |
|
|
|||||||||
i ← 1 |
|
|
|||||||||
result2,1 ← i |
|
|
|||||||||
result2,3 ← x2T |
|
|
|||||||||
|
|
|
→ |
|
|||||||
result1,2 ← max( |
|
r0 |
|
|
) |
|
|||||
|
|
|
|
||||||||
while 1 |
|
|
|||||||||
|
x1 ← x2 |
|
|
||||||||
|
|
|
|||||||||
|
r1 ← r0 − alf A p0 |
|
|||||||||
|
bet ← r1 r1 |
|
|
||||||||
|
|
|
r0 r0 |
|
|
||||||
|
p1 ← r1 + bet p0 |
|
|
||||||||
|
alf ← |
r1 r1 |
|
|
|
||||||
A p1 p1 |
|
|
|||||||||
|
|
|
|
|
|||||||
|
x2 ← x1 + alf p1 |
|
|
||||||||
|
r0 ← r1 |
|
|
||||||||
|
p0 ← p1 |
|
|
||||||||
|
i ← i + 1 |
|
|
||||||||
|
resulti+1,1 ← i |
|
|
||||||||
|
resulti+1,3 ← x2T |
|
|||||||||
|
|
|
|
→ |
|||||||
|
resulti,2 ← max( |
r0 |
) |
||||||||
|
|
||||||||||
|
break if i ≥ m |
|
|
||||||||
r1 ← r0 − alf A p0
→ resulti+1,2 ← max( r1 )
result
5
7. Проверка действия программ для m=3, n=5, матриц A, B и векторов b, c, рассчитанных для m=5 и единичного вектора начальных приближений из 5 элементов. Для метода релаксации ω =1,1.
Метод Якоби:
|
|
0 |
82.3718804 |
1 |
|
1 |
1 |
1 |
|
1 |
|
|||
|
|
1 |
59.8196007 0.6151325 0.2523783 0.2517585 0.3031223 0.7272788 |
|||||||||||
yukobi(3,5,x0,A ,b ,B,c) = |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
34.485779 |
0.9034207 0.6828392 0.7951418 0.6934455 0.9977866 |
|||||||||
|
|
3 |
25.8195136 0.7353441 0.3691627 0.4830494 0.3855308 0.8439448 |
|||||||||||
Метод Зейделя: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
82.3718804 |
|
1 |
|
1 |
1 |
1 |
|
1 |
|
|||
|
1 |
25.5195789 0.6151325 0.3937246 0.4815957 0.5059031 0.9189983 |
||||||||||||
zeid(3,5,x0,A ,b ,B,c) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
5.4957682 |
0.8472085 0.5089348 0.6185011 0.4829036 0.9246847 |
||||||||||
|
3 |
1.3130694 |
0.802474 |
0.4753754 0.6400048 |
0.473548 |
0.9277909 |
||||||||
Метод релаксации: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
82.3718804 |
1 |
|
1 |
1 |
1 |
|
1 |
|
|||
rel(3,5,x0,A ,b ,B,c, |
1.1) = |
1 |
31.6368436 0.5766457 0.3486452 0.4487465 0.4707734 0.9258233 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
10.4829469 |
0.893123 |
0.5204568 0.6440098 0.4707585 0.9289185 |
||||||||
|
|
3 |
3.2174206 |
0.7882575 0.4665278 0.6482963 0.4689472 |
0.929391 |
|||||||||
Метод сопряженных градиентов: |
|
|
|
|
|
|
|
|
|
|||||
0 |
82.3718804 |
|
|
|
|
( 1 1 1 |
1 1 ) |
|
|
|
|
|||
1 |
6.2251448 |
( 0.7666501 0.5467968 0.5458158 0.57738 0.8347036) |
|
|||||||||||
grad(3,x0,A ,b) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3.1412392 |
( 0.8113988 0.4718491 0.6126522 0.4941571 0.9492896) |
|
|||||||||||
3 |
0.7317604 |
( 0.8220672 0.4648687 0.6465822 0.4629329 0.9329113) |
|
|||||||||||
6

8. Таблица 1. Решение СЛАУ порядка m = 5.
Номер |
|
Норма невязки |
|
Норма невязки |
|
Норма невязки |
Норма невязки для |
|
итерации |
|
для метода |
|
для метода |
|
для метода SQR |
метода CG |
|
|
|
Якоби |
|
Зейделя |
|
при ω=1,1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
82.3718804 |
|
82.3718804 |
|
82.3718804 |
82.3718804 |
|
|
|
|
|
|
|
|
|
|
1 |
|
59.8196007 |
|
25.5195789 |
|
31.6368436 |
6.2251448 |
|
|
|
|
|
|
|
|
|
|
2 |
|
34.485779 |
|
5.4957682 |
|
10.4829469 |
3.1412392 |
|
|
|
|
|
|
|
|
|
|
3 |
|
25.8195136 |
|
1.3130694 |
|
3.2174206 |
0.7317604 |
|
|
|
|
|
|
|
|
|
|
4 |
|
15.069627 |
|
0.4748357 |
|
0.0474064 |
0.1968782 |
|
|
|
|
|
|
|
|
|
|
5 |
|
11.1376948 |
|
0.1691849 |
|
0.0197926 |
7.8201334*10^-15 |
|
|
|
|
|
|
|
|
|
|
6 |
|
6.6020427 |
|
0.062247 |
|
4.7339752*10^-3 |
0 |
|
|
|
|
|
|
|
|
|
|
10 |
|
1.2633238 |
|
1.2227787*10^-3 |
|
6.8273843*10^-6 |
0 |
|
|
|
|
|
|
|
|
|
|
15 |
|
0.1683223 |
|
9.1400055*10^-6 |
|
1.8506512*10^-9 |
0 |
|
|
|
|
|
|
|
|
|
|
20 |
|
0.0199908 |
|
6.834199*10^-8 |
|
4.9737992*10^-13 |
0 |
|
|
|
|
|
|
|
|
|
|
Таблица 2. Решение СЛАУ порядка m = 10. |
|
|
|
|
||||
|
|
|
|
|
Норма невязки для |
|
|
|
Номер |
|
Норма невязки |
|
Норма невязки |
Норма невязки |
|||
итерации |
|
для метода |
|
для метода |
|
метода SQR при |
для метода CG |
|
|
|
Якоби |
|
Зейделя |
|
ω=1,1 |
|
|
|
|
|
82.3859701 |
|
|
|||
0 |
82.3859701 |
82.3859701 |
82.3859701 |
|
||||
|
|
|
1.4128235 |
|
|
|||
4 |
31.5388678 |
0.9949374 |
1.9091779 |
|
||||
|
|
|
0.0706312 |
|
|
|||
7 |
8.6052029 |
0.093531 |
0.056911 |
|
||||
|
|
|
4.4476555*10^-3 |
|
|
|||
10 |
3.4123952 |
0.0108746 |
1.0168732*10^-15 |
|
||||
|
|
|
1.6408453*10^-3 |
|
|
|||
11 |
2.4812895 |
5.4082444*10^-3 |
0 |
|
||||
|
|
|
5.4857986*10^-4 |
|
|
|||
12 |
1.8411484 |
2.7473668*10^-3 |
0 |
|
||||
|
|
|
1.7252942*10^-5 |
|
|
|||
15 |
0.7253586 |
3.4263969*10^-4 |
0 |
|
||||
|
|
|
4.804663*10^-8 |
|
|
|||
20 |
0.2133492 |
8.2758462*10^-6 |
0 |
|
||||
|
|
|
4.5433524*10^-9 |
|
|
|||
22 |
0.0858819 |
1.7676234*10^-6 |
0 |
|
||||
|
|
|
1.1937118*10^-12 |
|
|
|||
29 |
0.0137599 |
7.1743216*10^-9 |
0 |
|
||||
|
|
|
3.6948222*10^-13 |
|
|
|||
30 |
7.4777144*10^-3 |
3.2480045*10^-9 |
0 |
|
||||
|
|
|
|
|
|
|
|
|
7

Таблица 3. Решение СЛАУ порядка m = 100.
Номер |
Норма невязки |
Норма невязки |
Норма невязки |
Норма невязки |
итерации |
для метода Якоби |
для метода |
для метода SQR |
для метода CG |
|
|
Зейделя |
при ω=1,1 |
|
|
|
|
|
|
0 |
9.9957553*10^4 |
9.9957553*10^4 |
9.9957553*10^4 |
9.9957553*10^4 |
|
|
|
|
|
10 |
6.0255085*10^3 |
7.1592019 |
4.4137716 |
5.4013765 |
|
|
|
|
|
20 |
415.8054455 |
8.4782202*10^-3 |
1.577451*10^-3 |
1.5267986*10^-3 |
|
|
|
|
|
35 |
7.8677214 |
5.3831172*10^-7 |
4.5110937*10^-9 |
9.6779317*10^-10 |
|
|
|
|
|
37 |
4.647257 |
1.5088881*10^-7 |
9.3859853*10^-10 |
1.6727035*10^-10 |
|
|
|
|
|
45 |
0.5655975 |
9.4587449*10^-10 |
2.910383*10^-11 |
1.459562*10^-13 |
|
|
|
|
|
50 |
0.1520457 |
6.5483619*10^-11 |
2.910383*10^-11 |
1.5562589*10^-15 |
|
|
|
|
|
80 |
5.8818878*10^-5 |
2.1827873*10^-11 |
2.910383*10^-11 |
0 |
|
|
|
|
|
100 |
3.1665695*10^-7 |
2.1827873*10^-11 |
2.910383*10^-11 |
0 |
|
|
|
|
|
120 |
1.724402*10^-9 |
2.1827873*10^-11 |
2.910383*10^-11 |
0 |
|
|
|
|
|
123 |
7.9307938*10^-10 |
2.1827873*10^-11 |
2.910383*10^-11 |
0 |
|
|
|
|
|
150 |
2.910383*10^-11 |
2.1827873*10^-11 |
2.910383*10^-11 |
0 |
|
|
|
|
|
Примечание: подчеркнуты номера значений и соответствующие им номера итераций, на которых невязка впервые уменьшается в К=1010 раз.
10. Выводы.
1) Сравнение номеров итерации, на которых невязка впервые уменьшается в К=1010 раз для рассматриваемых итерационных методов.
Порядок СЛАУ |
|
Номер итерации |
|
||
|
|
|
|
||
Метод Якоби |
Метод Зейделя |
Метод SQR |
Метод CG |
||
|
|||||
|
|
|
15 |
|
|
5 |
- |
- |
5 |
||
|
|
|
22 |
|
|
10 |
- |
29 |
10 |
||
|
|
|
37 |
|
|
100 |
123 |
45 |
35 |
||
|
|
|
|
|
|
8
2) Сравнение качества приближения на m-й итерации:
Для m=5, 10, 100 норма невязки метода CG равна нулю, то есть метод дает точное решение. Норма невязки для метода SQR при m=5, 10 меньше, чем норма невязки для методов Зейделя и Гаусса, то есть метод дает более приближенное к искомому решение на данном этапе. При m=100 норма невязки для метода Зейделя имеет наименьшее значение при сравнении методов Якоби, Зейделя и SQR, и показывает, что метод Зейделя дает более приближенное к искомому решение, чем другие два.
3) Результаты расчета уменьшения нормы невязки на m-й итерации и скорости сходимости методов Якоби и Зейделя.
Порядок СЛАУ |
Уменьшение нормы невязки на последней итерации (число раз) |
||||
|
|
|
|
||
Метод Якоби |
Метод Зейделя |
Метод SQR |
Метод CG |
||
|
|||||
|
|
|
16,56*1013 |
|
|
5 |
41,2*102 |
12,05*108 |
∞ |
||
|
|
|
22,3*1013 |
|
|
10 |
11,02*103 |
25,37*109 |
|
||
|
|
|
34,35*1014 |
|
|
100 |
34,35*1014 |
45,79*1014 |
|
||
Метод Якоби сходится со скоростью геометрической прогрессии со знаменателем q=||B||.
Для m=5:
normi(B) = 0.7719746 |
q=0,7719746 |
Практически полученное значение q ≈ 0,6 ÷0,77.
Метод Зейделя сходится со скоростью геометрической прогрессии со знаменателем q=||B2|| / (1-||B1||).
Для m=5:
normi(B1) = 0.3881792
normi(B2) = 0.3880162
0.3881792 |
|
= 0.6342965 |
|
1 − 0.3880162 |
|||
|
|||
q= 0,6342965
Практически полученное значение q ≈ 0,2 ÷0,54.
9
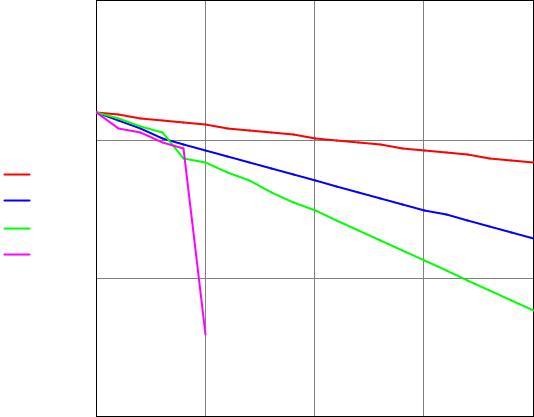
4)Введение значения релаксационного параметра в методе SQR оказалось достаточно эффективным по сравнению с методами Якоби и Зейделя - метод SQR сходится быстрее методов Зейделя и Якоби; и не эффективным по сравнению с методом сопряженных градиентов, так как сходится медленнее него.
5)Для СЛАУ порядка m=5 норма невязки в методе сопряженных градиентов перестала изменяться после 5-го шага, порядка m=10 – 10-го шага, порядка m=100 – 50-го шага. Шагов в методе сопряженных градиентов не может быть больше, чем количество неизвестных (не больше размерности пространства, в котором ищем решение).
11. Графики зависимости десятичного логарифма нормы невязки для различных |
||||||||
итерационных методов при m=20, n=5, матриц A, B и векторов b, c, рассчитанных для m=5 |
||||||||
и единичного вектора начальных приближений из 5 элементов: |
|
|||||||
|
|
|
|
0 |
|
|
|
|
log yukobi |
i |
,2) |
|
|
|
|
||
( |
|
|
|
|
|
|
||
log zeid |
i ,2) |
|
|
|
|
|
||
( |
|
|
|
|
|
|
||
log rel |
|
|
|
|
|
|
|
|
( |
i ,2) |
|
|
|
|
|
|
|
log grad |
|
|
|
|
|
|
||
( |
|
i ,2) |
|
|
|
|
|
|
|
|
|
|
− 10 |
|
|
|
|
|
|
|
|
− 200 |
5 |
10 |
15 |
20 |
|
|
|
|
|
|
reli ,1 |
|
|
|
|
|
|
|
|
|
|
10 |
