Правило сложения

Идея рассуждения – разбить все варианты на группы, каждая из которых состоит из «одинаково устроенных» комбинаций.

Пример

Сколько способов поставить двух шахматных королей на доску 8х8 так, чтобы они не «били» друг друга?

Решение.

В данном случае количество полей, которое «бьёт» король, зависит от его положения на доске.

Если он в углу (4 варианта), то для второго короля свободны 60 полей, если у края доски (24 варианта), то свободны 58 полей, а если отстоит не в углу и не у края (36 вариантов), то свободны 55 полей.

Таким образом, получим 4  60 + 24  58 + 36  55 = 3612. Разделив это количество пополам (по той же причине, что в предыдущем примере), получим 1806.

Перестановки

Перестановкой называют упорядоченный набор чисел 1, 2, 3, … n, возможно, переставленных в другом порядке – например, 3, 2, 1, 4, 5, 6, …, n.

Первый элемент перестановки можно выбрать n способами, тогда второй останется (n-1) способов, на третий – (n-2) способа, и так далее до заключительного элемента, для которого останется ровно один вариант.

Таким образом, количество перестановок равно n(n-1)(n-2) …  21 = n!

Примечание. n! здесь и далее обозначает произведение всех целых чисел от 1 до n. В задачах по комбинаторике принято оставлять в ответе факториалы, степени, произведения, поскольку число в ответе задачи может оказаться большим, и его вычисление займёт слишком много времени.

Пример.

Сколько способов посадить 5 человек на 5 стульев, по одному человеку на стул?

Размещения с повторениями

Размещение с повторениями – упорядоченный набор элементов, каждый из которых принадлежит данному множеству.

Если множество содержит n элементов, а наборы должны содержать k элементов, то каждый элемент можем выбрать n способами, всего элементов k, поэтому количество размещений с повторениями равно n^k.

Пример.

Сколько существует 4-значных чисел, все цифры в которых нечётны?

Размещения без повторений

Размещение без повторений – упорядоченный набор элементов, каждый из которых принадлежит данному множеству, и при этом все элементы набора должны быть различными.

Если множество содержит n элементов, а наборы должны содержать k элементов, то первый элемент можем выбрать n способами, второй (n-1) способом, и так далее до элемента номер k, его можем выбрать (n – k +1) способом. Поэтому количество размещений без повторений равно n(n - 1)…( n – k +1) = n! / (n-k)!

Пример.

Сколько существует 4-значных чисел, все цифры в которых нечётны и различны?

Сочетания

- число k-элементных подмножеств n-элементного множества (читается как «число сочетаний из n по k»).

Для нахождения количества сочетаний без повторений воспользуемся формулой для размещений без повторений.

Упорядоченных наборов k элементов из n существует n!/(n-k)! Если будем рассматривать неупорядоченные наборы, то каждый из них сосчитаем по k! раз.

Поэтому неупорядоченных наборов в k! раз меньше, чем упорядоченных.

Поэтому количество неупорядоченных наборов вычисляется по формуле: n!/((n-k)!k!).

Пример.

Сколько способов выбрать трёх дежурных из 25 человек?

Можно вычислять по формуле: 25!/(22!∙3!)

Можно и с помощью логических рассуждений. Первого дежурного можно выбрать 25 способами, второго – 24 способами, третьего – 22 способами. Всего получаем 25 ∙ 24 ∙ 22 способа.

Переход к дополнению

В некоторых случаях проще вычислить количество элементов, которые нам не подходят, а затем вычесть их количество из общего числа элементов.

Пример.

Сколько существует 5-значных чисел, в которых есть хотя бы одна чётная цифра?

Использование взаимно однозначного соответствия множеств

Пример.

Найти количество всех подмножеств множества из N элементов.

Решение. Обозначим каждое подмножество набором нулей и единиц, всего из N элементов. При этом на позиции номер i стоит 1, если элемент номер i содержится в подмножестве, и 0, если не содержится в нём.

Тогда различных наборов 2^N, поскольку на каждом из N мест может находиться или 0, или 1.

Количество подмножеств равно количеству наборов, поскольку подмножества и наборы нулей и единиц находятся во взаимно-однозначном соответствии.

Итак, количество подмножеств равно 2^N.

Ответ. 2^N.

Принцип включений исключений

Рассмотрим задачу.

Пример. Из 35 студентов 20 изучает английский язык, 15 – немецкий, 10 – французский, 7 – английский и немецкий, 5 – английский и французский, 4 – немецкий и французский, 3 – английский, французский и немецкий. Сколько студентов не изучает ни один из перечисленных языков?

Существует формула, называемая формулой включений-исключений, которая дает ответ на этот вопрос:

N(0)=N-(N1+N2+N3)+(N12+N13+N23)-N123.

Что она означает? N – общее число студентов. N1- число студентов, изучающих английский язык, N12 – английский и немецкий и т.д., N(0) – число студентов не изучающих ни один из перечисленных языков.

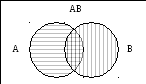
Для иллюстрации рассуждений такого типа используются рисунки, называемые диаграммами Венна.

Например, множество всех студентов в группе обозначено прямоугольником.

Множество А обозначает всех студентов, знающих немецкий язык, множество В – всех студентов, знающих английский язык. Множество АВ (в центре рисунка) обозначает множество студентов, знающих оба иностранных языка, заштрихованная часть рисунка – студентов, знающих хотя бы один иностранный язык.

Наконец, не заштрихованная часть внутри прямоугольника – множество студентов группы, не знающих ни одного иностранного языка.

Пример. В группе из 25 человек 16 человек знает французский язык, 22 знают английский язык, один не знает ни одного иностранного языка. Сколько студентов знают хотя бы один из двух иностранных языков?

Задача: Секретарь рассыпал письма из конвертов, и обратно положил их наугад, по одному письму в конверт. Найти вероятность того, что хотя бы одно письмо попадёт не в свой конверт.

Примечание: ответ практически не зависит от количества писем и приближённо равен 1 – 1/e, причём уже начиная с n = 6 совпадение с точностью до 4 знаков после запятой.

Бином Ньютона

(a + b)ⁿ =

Для доказательства формулы можно рассмотреть выражение (a + b) ∙ (a + b) ∙… ∙ (a + b). Подсчитаем, сколько раз в этом выражении встретится b^k.

Это выражение встретится столько раз, сколько способов выбрать k скобок, из которых возьмём b, среди всех n скобок. А это количество способов равно .

Из оставшихся (n-k) скобок выберем (n-k) множителей a. Таким образом, получим слагаемое . Так сделаем для k от 0 до n.

Свойства биномиальных коэффициентов

Доказательство.

Подставим в бином Ньютона a = b = 1.

Доказательство.

Подставим в бином Ньютона a = 1, b = -1.

Шары и перегородки

Рассмотрим задачу: сколько способов представить число n в виде суммы k натуральных слагаемых?

Можно представить её так: набор из n шаров, расположенных в ряд, разделить на k частей, поставив (k-1) перегородок.

В таком виде задача гораздо понятнее, поскольку мы должны выбрать (k-1) мест из (n-1) возможных. А количество сделать это мы знаем - .

Пример.

Сколько способов представить 10 в виде суммы шести натуральных слагаемых?

Решение.

Представим формулировку в таком виде: разбить цепочку из 10 шаров на шесть групп. Для этого достаточно разместить пять перегородок в 9 промежутках. (НАРИСОВАТЬ!)

Это можно сделать способами.

Ответ: .

Можно усложнить задачу: сколько способов представить число n в виде суммы k целых слагаемых, каждое из которых не меньше m?

Эту задачу можно свести к предыдущей: для случая m = 1 решать задачу мы умеем, а для общего случая для x_i ≥ m (при i = 1, 2, …, k) можно сделать замену y_i = x_i – m + 1. Получим задачу для чисел y₁, y₂, … y_k, сумму которых мы можем вычислить:

y₁ + y₂ + … + y_k = (x₁ – m + 1) + (x₂ – m + 1) + … + (x_k – m + 1) = (x₁ + x₂ + … + x_k) + k(-m+1) = n – km + k.

Таким образом, все числа y_i натуральные, причём их сумма известна. Такую задачу мы решать уже умеем.

Пример.

Сколько способов представить 100 в виде суммы шести натуральных слагаемых, каждое из которых не меньше 3?

Если каждое из чисел не меньше 1 (то есть натуральное), то способов будет (5 перегородок в 99 промежутков).

Если по условию все , можем сделать замену y_i = x_i – 2, тогда все , то есть получили задачу для суммы натуральных чисел. При этом сумма всех y_i будет на 12 меньше суммы всех x_i, то есть будет равна 100 – 12 = 88.

Итак, получили задачу: сколько способов представить число 88 в виде шести натуральных слагаемых? Такую задачу мы умеем решать. Ответ в данном случае будет равен .

Пример.

Сколько способов представить 100 в виде суммы шести натуральных слагаемых, каждое из которых не меньше -4?

Если по условию все , можем сделать замену y_i = x_i + 5, тогда все , то есть получили задачу для суммы натуральных чисел. При этом сумма всех y_i будет на 30 больше суммы всех x_i, то есть будет равна 100 +30 = 130.

Сколько способов представить число 130 в виде шести натуральных слагаемых?

Ответ: .