
- •Обобщённый алгоритм Евклида
- •Второй способ нахождения линейного представления наибольшего общего делителя
- •Линейные диофантовы уравнения с двумя неизвестными
- •Решение уравнений в кольце остатков по данному модулю
- •Китайская теорема об остатках (теория)
- •Непрерывные дроби и перевод рационального числа в конечную дробь
- •Наилучшие приближения
- •Разбор типовых примеров к первому индивидуальному домашнему заданию по теме «Делимость целых чисел и многочленов»
- •Второй способ решения диофантова уравнения
- •Правило сложения
- •Перестановки
- •Треугольник Паскаля
- •Серия задач по комбинаторике на различные методы решения
- •Определение
- •Упражнение 1. Приведите пример двудольного графа с 6 вершинами. Упражнение 2. Докажите признаки двудольных графов:
- •Булевы функции
- •Многочлен Жегалкина
- •Двойственная функция
- •Нахождение таблицы значений функции, двойственной к данной булевой функции
- •Исследование булевой функции на принадлежность к основным классам замкнутости
- •Применение теоремы Пóста
- •Представление конъюнкции и отрицания через данную функцию f (X, y, z) и её отрицание
Непрерывные дроби и перевод рационального числа в конечную дробь
Определение
Непрерывной дробью называют дробь вида
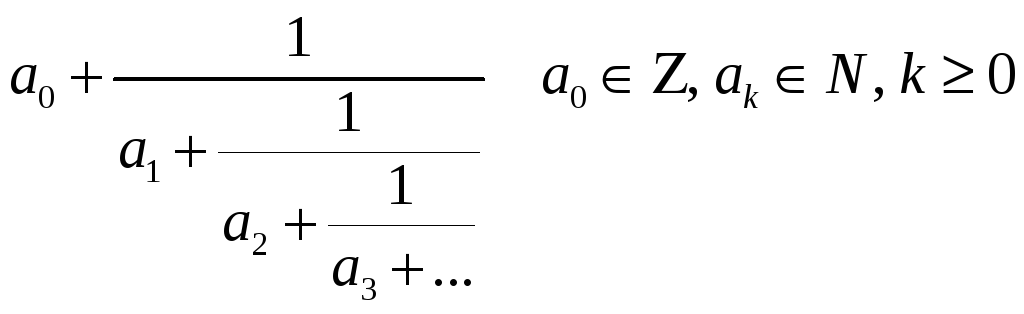
Если эта дробь где-либо заканчивается, её называют конечной непрерывной дробью.
Конечные непрерывные дроби соответствуют рациональным числам.
Пример.
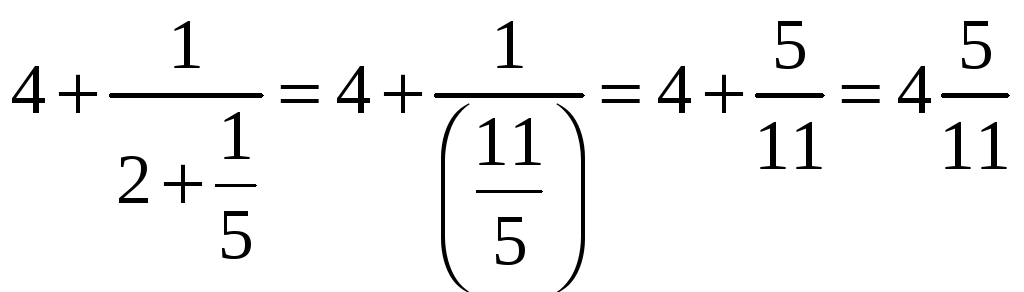
Возможно и обратное действие: получение непрерывной дроби из рационального числа.
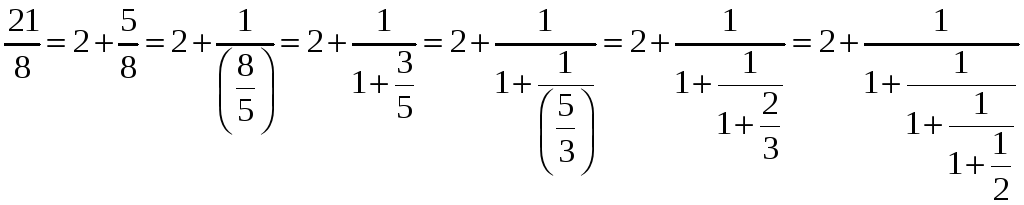
Обычно такую непрерывную дробь записывают в виде (2; 1, 1, 1, 2). Целая часть отделяется точкой с запятой.
Теперь покажем другой способ нахождения коэффициентов непрерывной дроби. Применим алгоритм Евклида к числам 21 и 8.
21 = 8 ∙ 2 + 5
8 = 5 ∙ 1 + 3
5 = 3 ∙ 1 + 2
3 = 2 ∙ 1 + 1
2 = 1 ∙ 2
Обратите внимание на связь коэффициентов непрерывной дроби с неполными частными в алгоритме Евклида!
Если у этой дроби начиная с некоторого места образуется период, её называют периодической непрерывной дробью.
Периодическую непрерывную дробь можно выразить в виде корня некоторого квадратного уравнения.
Пример.
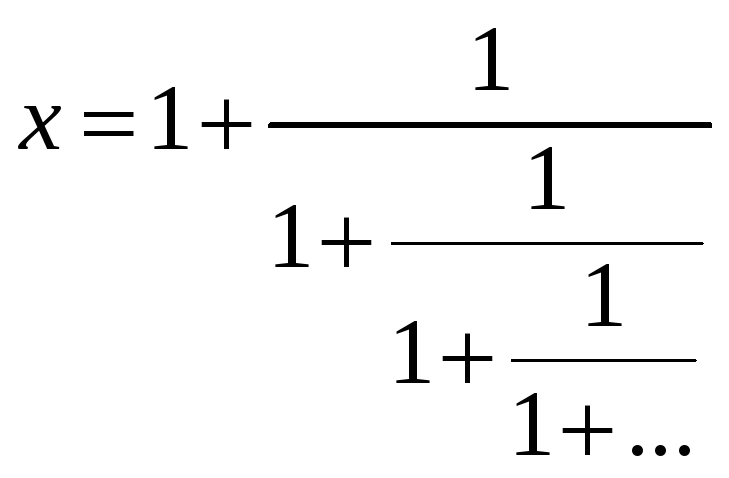
Тогда
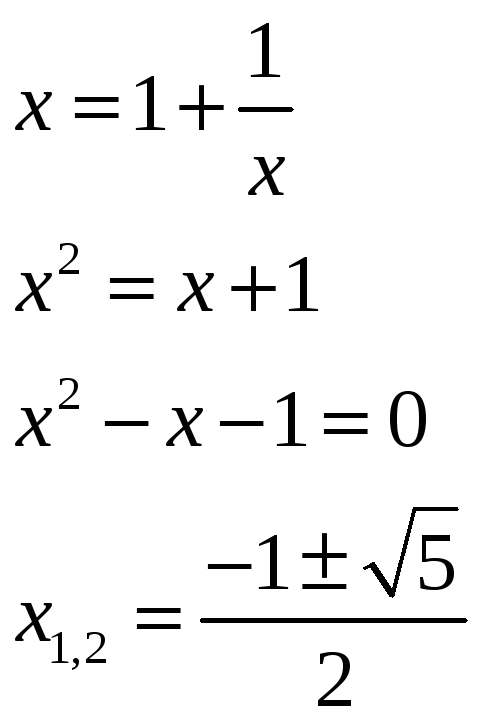
Поскольку число положительное, из двух значений берём положительное.
![]()
Можно получить разложение иррационального числа в периодическую дробь следующим способом.
a0 равно целой части некоторого числа α.
Поэтому
![]()
Далее заметим, что a1 равно целой части числа α1.
![]()
Далее, a2 равно целой части числа α2, и так далее, пока не получим цикл, то есть равенство вида αk = αn. Это означает, что получен период.
Для чисел, являющихся корнями квадратных уравнений (в том числе для квадратных корней из натуральных чисел) период получится обязательно.
Пример.
Пусть
![]() .
.
Целая часть α равна 1. Поэтому
![]()
Целая часть α1 равна 1.
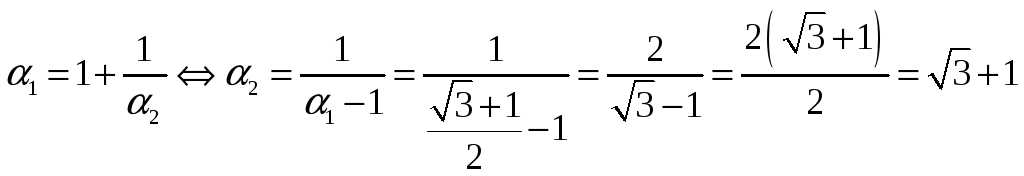
Примечание.
В задачах такого вида целую часть нужно искать именно домножением на сопряжённые, а не на калькуляторе, потому что для больших целых чисел, например, для трёхзначных, может накопиться ошибка округления, и значения целой части найдёте неверно.
Целая часть α2 равна 2.
![]()
Образовался цикл.
![]()
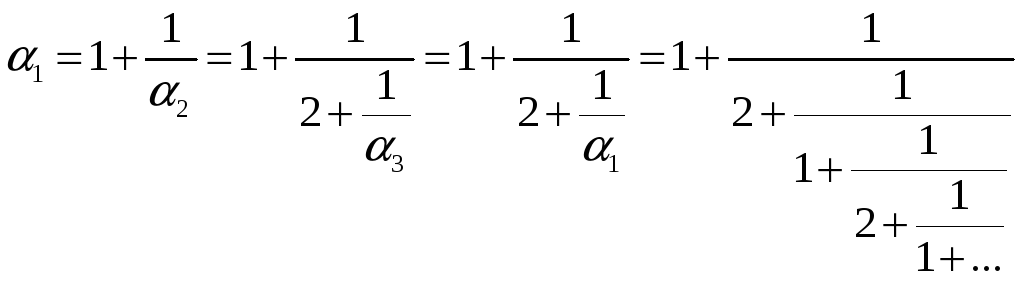
Ответ для периодической непрерывной дроби записывают в виде:
![]()
При этом целая часть отделена точкой с запятой, а период заключён во внутренние скобки.
Подходящей непрерывной дробью для данного числа α называют непрерывную дробь, которую мы оборвали на одном из коэффициентов. Для вычислений на практике, разумеется, так обычно и поступают.
Наилучшие приближения
На первый взгляд, непрерывные дроби могут показаться всего-навсего искусственно придуманным математическим объектом с неудобной формой записи.
Но приведём формулировку одной теоремы, чтобы стало понятно, где такие дроби можно применить.
Определение.
Наилучшим приближением числа α для дробей со знаменателем, не превышающим данное число n, называют рациональное число со знаменателем, не превышающим n, модуль разности которого с числом α наименьший.
Теорема (без доказательства).
Наилучшим приближением данного вещественного числа является одна из подходящих непрерывных дробей.
Разбор типовых примеров к первому индивидуальному домашнему заданию по теме «Делимость целых чисел и многочленов»
1. Диофантовы уравнения.
Решите диофантово уравнение 903x + 994 y = 14
Сначала найдём наибольший общий делитель коэффициентов в левой части, то есть НОД (903, 994).
Применим алгоритм Евклида.
994 = 903 ∙ 1 + 91
903 = 91 ∙ 9 + 84
91 = 84 ∙ 1 + 7
84 = 7 ∙ 12
Таким образом, НОД (903, 994) = 7.
Разделим обе части уравнения 903x + 994 y = 14 на 7.
Получим 129 x + 142 y = 2.
Найдём пару целых чисел x и y, таких, что 129 x + 142 y = 1.
Для этого воспользуемся обобщённым алгоритмом Евклида.
Сначала найдём НОД (129, 142) (мы уже знаем, что он равен 1, но результаты вычислений понадобятся нам для промежуточных выкладок).
142 = 129 ∙ 1 + 13
129 = 13 ∙ 9 + 12
13 = 12 ∙ 1 + 1
12 = 1 ∙ 12
Теперь эти выкладки рассматриваем от конца к началу, то есть выразим 1 как линейную комбинацию 13 и 12, затем – как линейную комбинацию 129 и 13, и, наконец, как линейную комбинацию 142 и 129.
1 = 13 – 12 = 13 – (129 – 13 ∙ 9) = 13 – 129 + 13 ∙ 9 = 13 ∙ 10 – 129 = (142 - 129) ∙ 10 – 129 = 142 ∙ 10 – 129 ∙11
Итак, мы нашли
![]() и
и
![]() такие, что
такие, что
![]() .
.
Но, поскольку уравнение имеет вид 129 x
+ 142 y = 2, то два найденных
числа умножим на 2, то есть в качестве
частного решения возьмём
![]() и
и
![]() .
.
Теперь найдём общее решение. Если в уравнении 129 x + 142 y = 2 величину x уменьшить на 142, а величину y увеличить на 129, то сумма не изменится, поскольку величина 129 ∙ 142 к одному слагаемому прибавляется, а из другого слагаемого вычитается.
Поэтому можем общее решение записать так.
x = -22 – 142 t, y = 20 + 129 t, t – произвольное целое число.
Это и будет ответом.
Ответ. x = -22 – 142 t, y = 20 + 129 t, t – произвольное целое число.
Примечание 1.
Если в условии стоит не сумма, а разность, например, 129 x – 142 y = 2, то величины 142 t и 129 t нужно будет брать с одним знаком, поскольку в этом случае увеличение чисел 129 x и 142 y будет происходить на одно и то же число. Поэтому их разность не изменится.
Примечание 2.
В этой задаче, как и во многих других задачах данной серии, можно проверить свой ответ, подставив числа в исходное уравнение или в уравнение 129 x + 142 y = 2 (если вы уверены, что правильно сократили).
Подставим их.
129(-22 – 142 t) + 142 (20 + 129 t) = 129 ∙ (-22) – 129 ∙ 142 t + 142 ∙ 20 + 142 ∙ 129 t = 129 ∙ (-22) + 142 ∙ 20 = 2.
При этом, если вы не учли примечание 1 и ошиблись со знаками, то при проверке это сразу увидите.
