
- •Методы вычисления пределов
- •Предел функции
- •Окрестность точки
- •Предел функции в точке. Непрерывность функции в точке
- •Предел функции на бесконечности
- •Бесконечно большая и бесконечно малая функции
- •Односторонние пределы
- •Элементарные функции
- •Вычисление пределов
- •Правила предельного перехода
- •Предел дробно-рациональной функции
- •Предел функций, содержащих иррациональные выражения
- •Замечательные пределы. Эквивалентные бесконечно малые функции
- •Пределы, содержащие тригонометрические функции
- •Пределы выражений, содержащих показательную, логарифмическую и степенную функции
- •Предел показательно-степенной функции
- •197376, С.-Петербург, Проф. Попова, 5
Замечательные пределы. Эквивалентные бесконечно малые функции
При решении практических задач используются замечательные пределы [1, с. 123, 124]:
 – первый замечательный предел;
(2.8)
– первый замечательный предел;
(2.8)
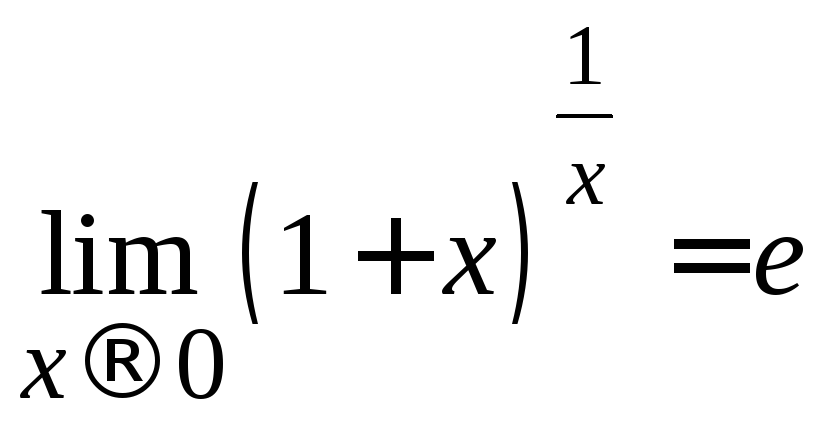 – второй замечательный предел.
(2.9)
– второй замечательный предел.
(2.9)
Замечательные пределы позволяют установить ряд полезных предельных соотношений:
1)
![]() ;
2)
;
2)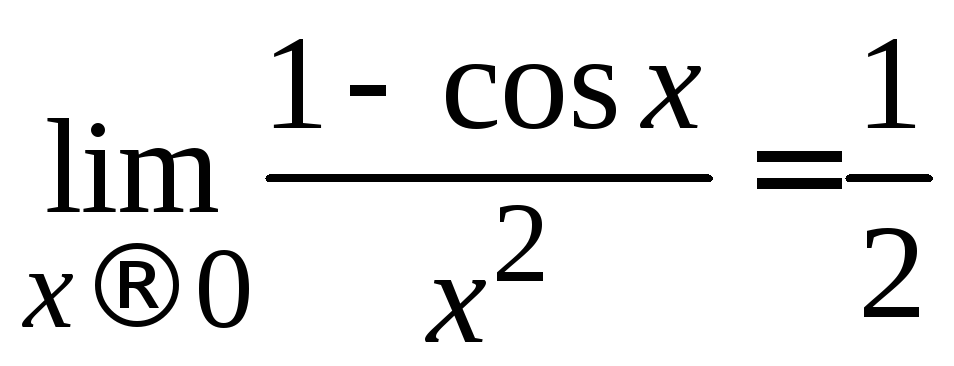 ;
3)
;
3)![]() ;
;
4)
![]() ;
5)
;
5)![]() ;
6)
;
6)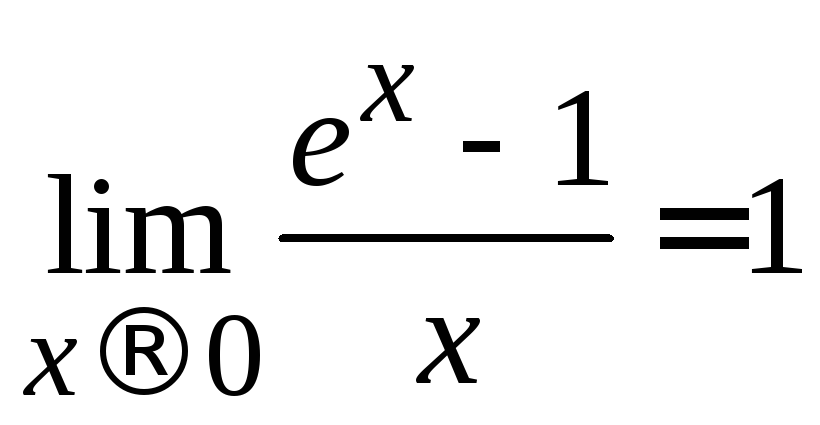 ;
;
7)
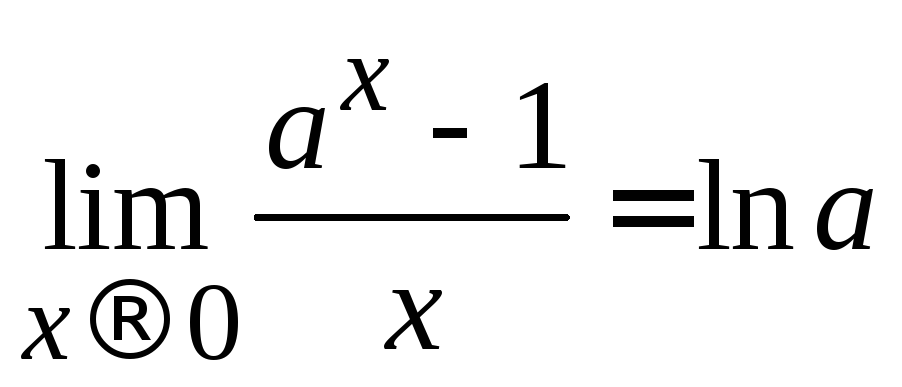 ;
8)
;
8)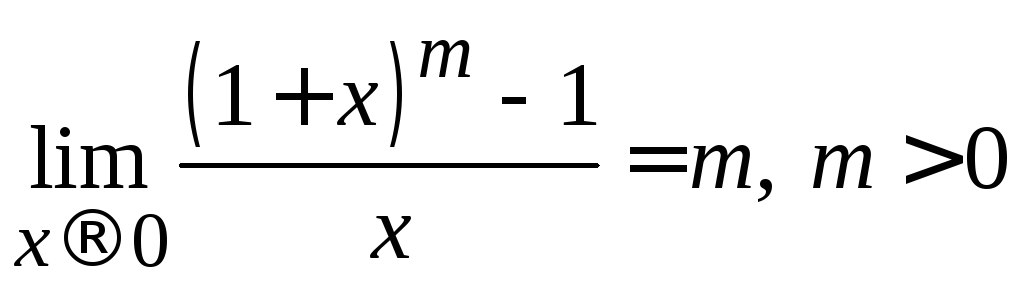 .
.
Пример 2.16. Вычислить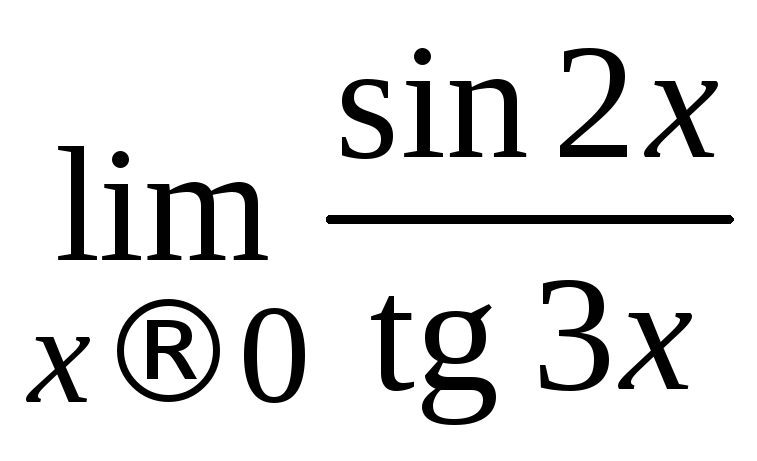 .
.
Решение.Сначала найдем предел![]() .
Для решения предложенной задачи сделаем
замену
.
Для решения предложенной задачи сделаем
замену![]() .
Новая переменная
.
Новая переменная![]() ,
когда
,
когда![]() .
Тогда в силу первого замечательного
предела имеем:
.
Тогда в силу первого замечательного
предела имеем:
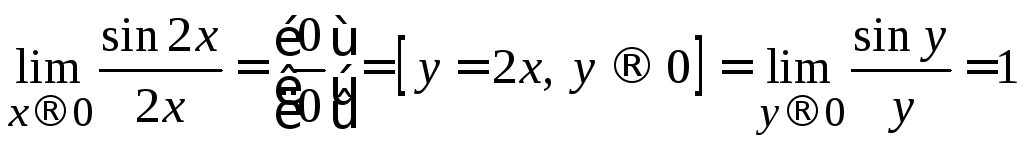 .
.
Рассуждая аналогичным образом, и
учитывая, что
![]() ,
находим:
,
находим:
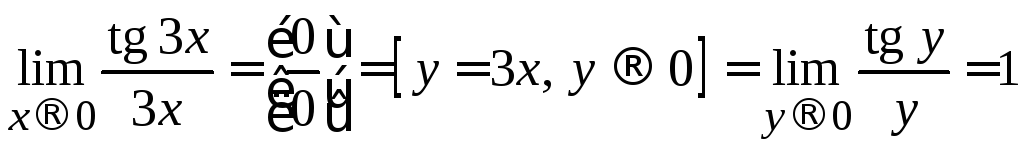 .
.
В числителе исходной дроби выделим
выражение
![]() ,
а в знаменателе выражение
,
а в знаменателе выражение![]() и применим формулы (2.3), (2.4). Тогда
и применим формулы (2.3), (2.4). Тогда
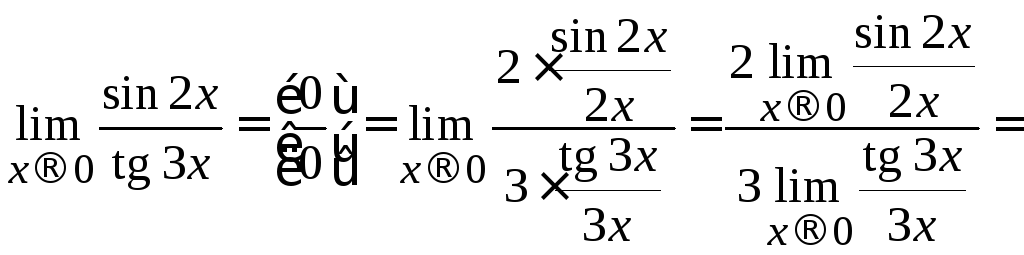
![]() .
.
Пусть
![]() и
и![]() есть бесконечно малые функции при
есть бесконечно малые функции при![]() ,
т. е.
,
т. е.![]() и
и![]() .
Функции
.
Функции![]() и
и![]() называются эквивалентными бесконечно
малыми при
называются эквивалентными бесконечно
малыми при![]() ,
если
,
если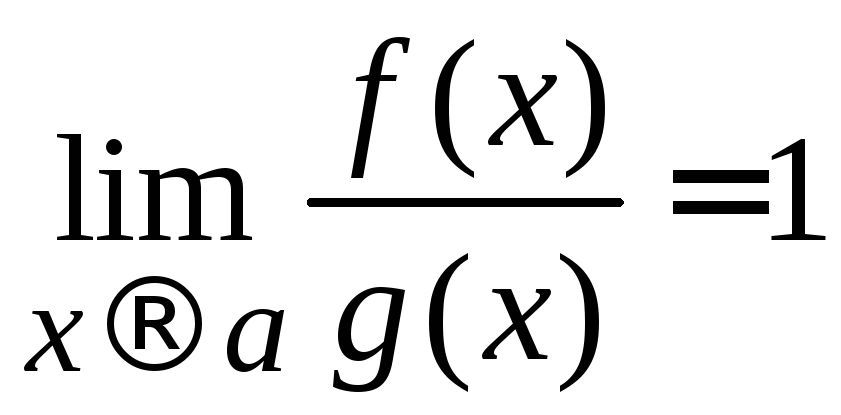 .
Обозначается это так:
.
Обозначается это так:![]() .
.![]()
Используя формулу (2.8) и предельные
соотношения 1 – 8, составим таблицу
важнейших эквивалентных бесконечно
малых функций при
![]() .
.
З амечание.
В качестве аргумента бесконечно
малых функций в таблице эквивалентностей
может выступать не только
амечание.
В качестве аргумента бесконечно
малых функций в таблице эквивалентностей
может выступать не только![]() ,
но и любая величина
,
но и любая величина![]() при
при![]() .
.
Поясним сказанное на примерах.
Пример 2.17. Найти бесконечно малые, эквивалентные функциям:
1)
![]() при
при![]() ;
2)
;
2)![]() при
при![]() ;
3)
;
3)![]() при
при![]() .
.
Решение:
1. Выражение
![]() при
при
![]() .Поэтому в роли бесконечно малого
аргумента показательной функции из
таблицы эквивалентностей выступает
величина
.Поэтому в роли бесконечно малого
аргумента показательной функции из
таблицы эквивалентностей выступает
величина![]() .
Следовательно,
.
Следовательно,![]() при
при![]() .
.
2. Рассматриваемая функция действительно
является бесконечно малой:
 .
Выражение
.
Выражение![]() при
при![]() ,
следовательно:
,
следовательно:![]() при
при![]() .
.
3. Проверкой убеждаемся, что
![]() .
В аргументе логарифма выделим единицу:
.
В аргументе логарифма выделим единицу:![]() .
Выражение
.
Выражение![]() при
при![]() .
Тогда по таблице эквивалентностей
имеем:
.
Тогда по таблице эквивалентностей
имеем:![]() при
при![]() .
.
Пример 2.18. Вычислить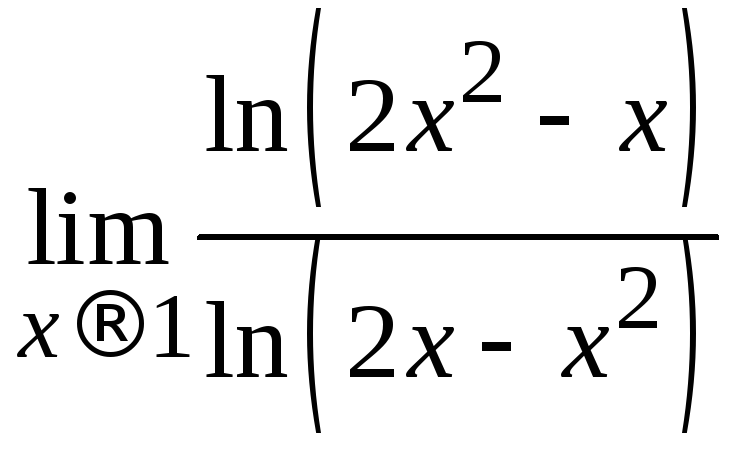 .
.
Решение. Подстановкой убеждаемся,
что имеет место неопределенность![]() ,
для раскрытия которой применим следующее
утверждение.
,
для раскрытия которой применим следующее
утверждение.
Теорема 2.1.Предел отношения двух бесконечно малых функций не изменится, если каждую или одну из них заменить эквивалентной ей бесконечно малой.
И
числитель, и знаменатель дроби –
бесконечно малые. В примере 2.17 определена
бесконечно малая, эквивалентная
числителю:
![]() при
при![]() .
Рассуждая аналогичным образом, получаем:
.
Рассуждая аналогичным образом, получаем:![]() при
при![]() .
После замены числителя и знаменателя
найденными эквивалентными бесконечно
малыми, придем к пределу отношения двух
многочленов:
.
После замены числителя и знаменателя
найденными эквивалентными бесконечно
малыми, придем к пределу отношения двух
многочленов:
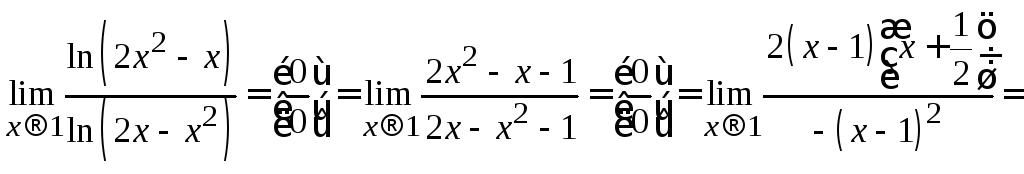
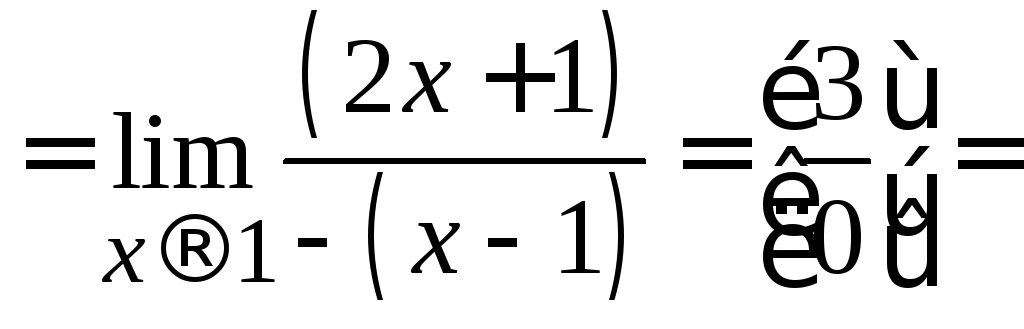
![]() .
.
Замечание. Предел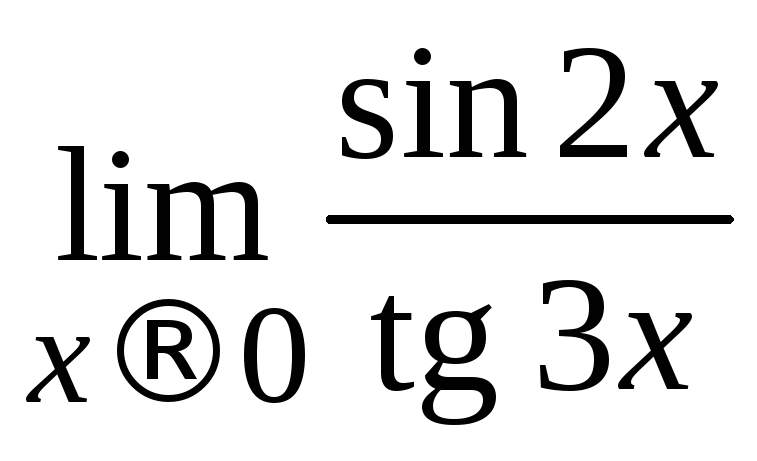 (пример 2.16) можно вычислить значительно
быстрее, если заменить числитель и
знаменатель эквивалентными им бесконечно
малыми. Так как
(пример 2.16) можно вычислить значительно
быстрее, если заменить числитель и
знаменатель эквивалентными им бесконечно
малыми. Так как![]() ,
а
,
а![]() при
при![]() ,
то
,
то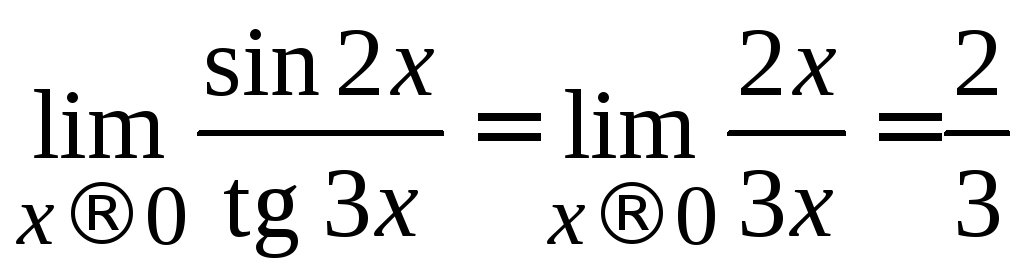 .
.
Согласно теореме 2.1, замена по таблице эквивалентностей разрешена в частном и произведении бесконечно малых функций, а вот в сумме или разности бесконечно малых функций она не законна. Однако некоторые пределы, содержащие сумму или разность бесконечно малых, можно вычислить, если перед тем, как осуществлять замену эквивалентными, воспользоваться теоремой о пределе суммы.
Пример 2.19. Вычислить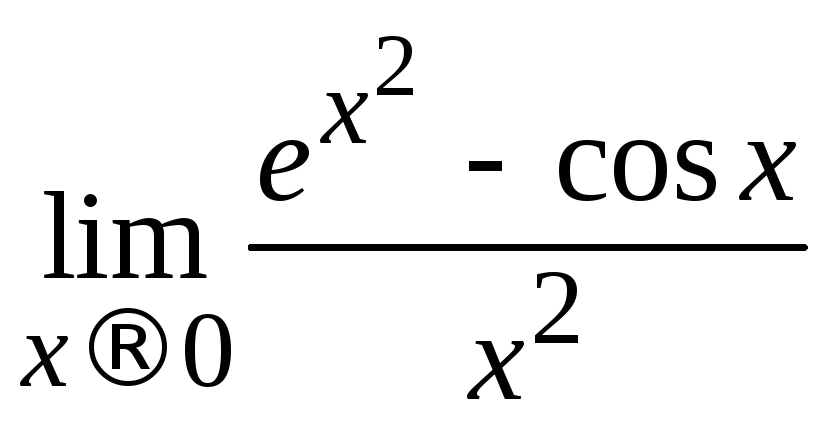 .
.
Решение. Преобразуем выражение,
стоящее под знаком предела, следующим
образом: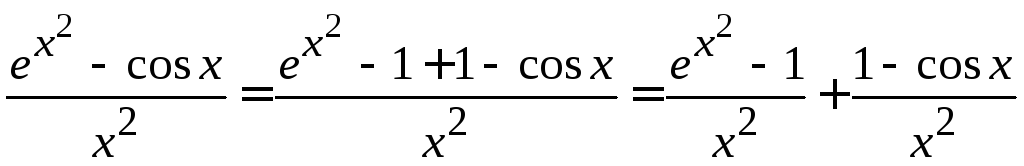 .
По таблице эквивалентностей:
.
По таблице эквивалентностей:![]() и
и![]() при
при![]() .
Тогда, применив теорему о пределе суммы
и заменив бесконечно малые эквивалентными
уже в отношениях, получим:
.
Тогда, применив теорему о пределе суммы
и заменив бесконечно малые эквивалентными
уже в отношениях, получим:
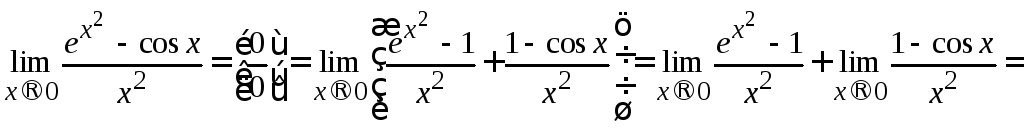
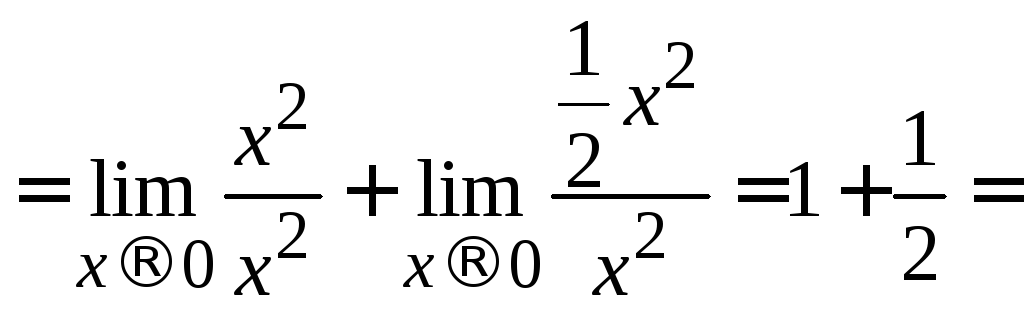
![]() .
.![]()
Но даже предварительное применение теоремы о пределе суммы или разности не гарантирует уничтожения неопределенности. Например,
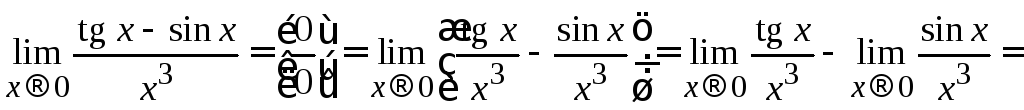
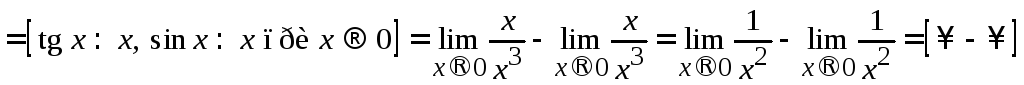 .
.
