
- •Методы вычисления пределов
- •Предел функции
- •Окрестность точки
- •Предел функции в точке. Непрерывность функции в точке
- •Предел функции на бесконечности
- •Бесконечно большая и бесконечно малая функции
- •Односторонние пределы
- •Элементарные функции
- •Вычисление пределов
- •Правила предельного перехода
- •Предел дробно-рациональной функции
- •Предел функций, содержащих иррациональные выражения
- •Замечательные пределы. Эквивалентные бесконечно малые функции
- •Пределы, содержащие тригонометрические функции
- •Пределы выражений, содержащих показательную, логарифмическую и степенную функции
- •Предел показательно-степенной функции
- •197376, С.-Петербург, Проф. Попова, 5
Федеральное агентство по образованию
___________________________________
Санкт-Петербургский государственный
электротехнический университет «ЛЭТИ»
_______________________________________
Методы вычисления пределов
Методические указания
к решению задач
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
2008
УДК 517
Методы вычисления пределов: Методические указания к решению задач / Сост.: Ю. В. Крашенинникова, М. Н. Абрамова. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2008. 32 с.
Содержат определения, формулировки основных теорем и примеры решения задач различными методами по теме «Предел функции».
Предназначены для студентов-заочников всех специальностей.
Утверждено
редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ «ЛЭТИ», 2008
Настоящее издание призвано помочь студентам-заочникам младших курсов самостоятельно научиться решать задачи по теме «Предел функции». Как правило, освоение этого раздела математического анализа вызывает затруднения у студентов. Поэтому первая часть методических указаний посвящена подробному обсуждению понятия «предел функции» и основных правил предельного перехода, причем все определения предела сопровождаются геометрической иллюстрацией. Во второй части указаний рассматриваются методы вычисления некоторых типов пределов.
Данные методические указания, хотя и содержат теоретический материал, не призваны служить полной заменой учебника по теме «Предел функции», поэтому составители рекомендуют параллельно работать с учебным пособием «Конспект лекций по высшей математике» Д. Т. Письменного [1].
Предел функции
Окрестность точки
Пусть
![]() – действительное число. Обозначение:
– действительное число. Обозначение:![]() .
.
Определение. Окрестностью точки ![]() радиуса
радиуса![]() (
(![]() -окрестностью)
н
-окрестностью)
н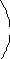

![]()
![]()
![]()
![]() ,
где
,
где![]() .
.
Е сли
точка
сли
точка![]() попадает в
попадает в![]() -окрестность
точки
-окрестность
точки![]() ,
т. е.
,
т. е.![]() ,
то выполнено неравенство
,
то выполнено неравенство![]() или
или![]() .
Последнее двойное неравенство равносильно
неравенству
.
Последнее двойное неравенство равносильно
неравенству![]() ,геометрический смысл которого
состоит в том, что расстояние между
точками
,геометрический смысл которого
состоит в том, что расстояние между
точками![]() и
и![]() меньше чем
меньше чем![]() (рис. 1.1).
(рис. 1.1).
Окрестность без точки
![]() называется проколотой окрестностью.
Она задается неравенством
называется проколотой окрестностью.
Она задается неравенством![]() ,
причем
,
причем![]() .
.
В дальнейшем рассматривается поведение
функций не только в окрестности точки
![]() ,
но и на бесконечности. Символы
,
но и на бесконечности. Символы![]() ,
,![]() используются для обозначения процесса
неограниченного удаления точек числовой
оси от нуля вправо и влево соответственно.
Иногда символ бесконечности употребляют
без уточнения знака.
используются для обозначения процесса
неограниченного удаления точек числовой
оси от нуля вправо и влево соответственно.
Иногда символ бесконечности употребляют
без уточнения знака.
Определение. Окрестностью![]() называется бесконечный интервал
называется бесконечный интервал![]() ,
а окрестностью
,
а окрестностью![]() – интервал
– интервал![]() ,
где
,
где![]() .
.
Е сли
точка
сли
точка![]() принадлежит окрестности
принадлежит окрестности![]() ,
то выполнено неравенство
,
то выполнено неравенство![]() ,
если же точка
,
если же точка![]() попадает в окрестность
попадает в окрестность![]() ,
то для нее справедливо неравенство
,
то для нее справедливо неравенство![]() .
Объединение лучей
.
Объединение лучей![]() будем рассматривать как окрестность
будем рассматривать как окрестность![]() (об операциях над множествами см. в [1,
с. 97]). Совокупность описывающих это
множество неравенств
(об операциях над множествами см. в [1,
с. 97]). Совокупность описывающих это
множество неравенств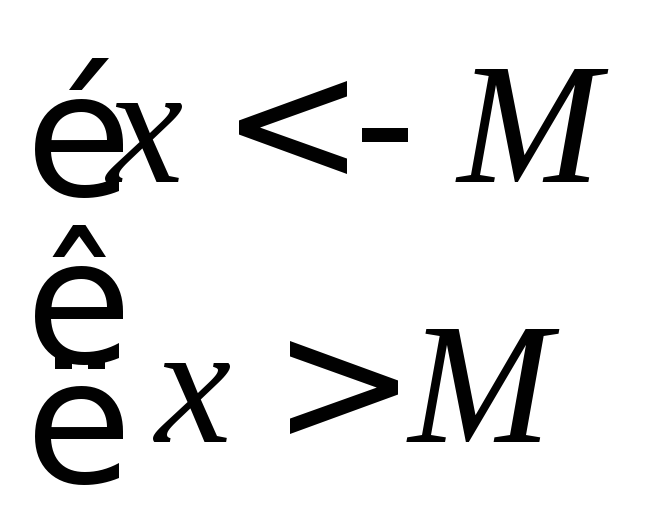 можно заменить одним неравенством
можно заменить одним неравенством![]() ,
означающим, что расстояние от точки
,
означающим, что расстояние от точки![]() до точки
до точки![]() больше чем
больше чем![]() (рис. 1.2).
(рис. 1.2).
Предел функции в точке. Непрерывность функции в точке
Пусть функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() ,
кроме, быть может, самой точки
,
кроме, быть может, самой точки![]() (о функции см. в [1, с. 100]).
(о функции см. в [1, с. 100]).
Определение предела функции на «языке
![]() »
см. в [1, с. 112]. Обозначение:
»
см. в [1, с. 112]. Обозначение:![]() .
Запишем это определение коротко:
.
Запишем это определение коротко:
![]() .
.
К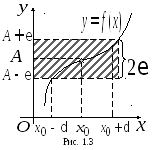 вантор
всеобщности
вантор
всеобщности![]() читается: «для всех». Квантор существования
читается: «для всех». Квантор существования![]() заменяет слово «существует». Запись
заменяет слово «существует». Запись![]() означает, что «из
означает, что «из![]() следует
следует![]() ».
А
».
А![]() указывает на эквивалентность высказываний
указывает на эквивалентность высказываний![]() и
и![]() ,
т. е. «из
,
т. е. «из![]() следует
следует![]() и из
и из![]() следует
следует![]() ».
».
Геометрический смыслпредела
функции поможет понять рис. 1.3. Для любой![]() -окрестности
точки
-окрестности
точки![]() (ось
(ось![]() )
найдется такая
)
найдется такая![]() -окрестность
точки
-окрестность
точки![]() (ось
(ось![]() ),
что для всех точек этой окрестности,
кроме, быть может,
),
что для всех точек этой окрестности,
кроме, быть может,![]() ,
соответствующие значения функции
,
соответствующие значения функции![]() лежат в
лежат в![]() -окрестности
точки
-окрестности
точки![]() .
Иначе говоря, точки графика функции
.
Иначе говоря, точки графика функции![]() лежат внутри полосы шириной
лежат внутри полосы шириной![]() ,
ограниченной прямыми
,
ограниченной прямыми![]() ,
,![]() .
Величина
.
Величина![]() зависит от выбора
зависит от выбора![]() ,
поэтому пишут
,
поэтому пишут![]() .
.
Пусть функция
![]() определена в точке
определена в точке![]() и в некоторой окрестности этой точки.
и в некоторой окрестности этой точки.
Определение.Функция![]() называется непрерывной в точке
называется непрерывной в точке![]() ,
если существует предел функции в этой
точке и он равен значению функции в
этой точке, т. е.
,
если существует предел функции в этой
точке и он равен значению функции в
этой точке, т. е.![]() .
.
Если на рис. 1.3 устранить разрыв функции
в точке
![]() ,
положив
,
положив![]() ,
то функция
,
то функция![]() окажется непрерывной в этой точке.
окажется непрерывной в этой точке.
