§2. Решение систем линейных уравнений методом Гаусса

Подробное описание метода Гаусса решения СЛУ можно найти на стр. 26-29, ч.1, [3].

Метод Гаусса заключается в приведении СЛУ к ступенчатому (в частности, к треугольному) виду при помощи элементарных преобразований над уравнениями системы. Например, если в системе менять местами уравнения, складывать их, умножать на не равные нулю числа, то мы получим равносильную СЛУ. Приведение СЛУ к ступенчатому виду называют «прямым ходом» метода Гаусса. «Обратным ходом» метода Гаусса называют последовательное определение неизвестных из этой ступенчатой системы. Все эти преобразования можно проводить как с уравнениями, записанными в СЛУ, так и с расширенной матрицей системы.

В качестве некоторых примеров будем рассматривать разрешимые системы уравнений из предыдущего параграфа.

1. Исследовать и решить СЛУ

Решение:

Удобно приводить к ступенчатому виду не саму систему уравнений, а ее расширенную матрицу. Попутно решается вопрос о совместности СЛУ. В нашем случае:

.

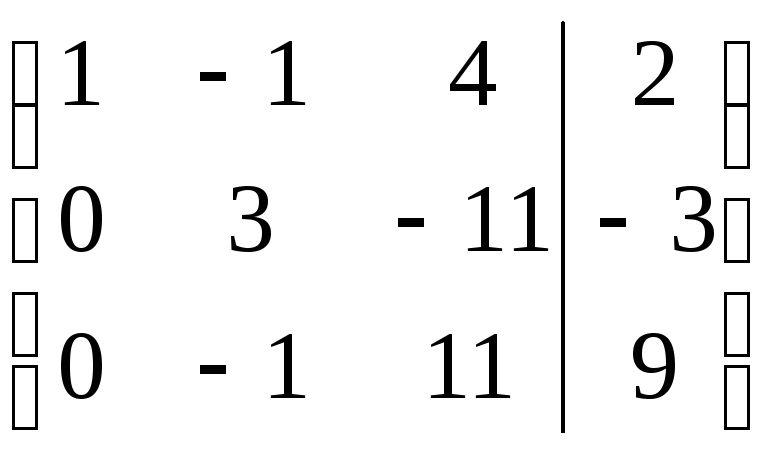
Ранг основной матрицы равен рангу расширенной и равен 3, следовательно, система совместна. При этом ранг совпадает с числом неизвестных, то есть СЛУ имеет единственное решение.

Исходная СЛУ равносильна системе

из которой следует Ответ:.

2. Исследовать и решить СЛУ

Решение:

Запишем расширенную матрицу СЛУ и приведем ее к ступенчатому виду: . Ранг расширенной матрицы 3, а ранг основной матрицы равен 2, следовательно, СЛУ несовместна. Это же показывает и последняя строка (0 0 0–3), которой соответствует уравнение 0x¹ + 0x² + 0x³= –3 или 0 = –3.

3. Решить систему:

Решение:

Выполним «прямой ход» метода Гаусса. Приведем расширенную матрицу к ступенчатому виду:

.

Ранги основной и расширенной матриц равны 3 и совпадают с числом неизвестных, то есть система совместна и имеет единственное решение.

«Обратный ход» метода Гаусса можно выполнять, используя полученную уже ступенчатую матрицу: 

. Для записи ответа можно использовать одну из следующих форм: или

4. Решить систему

Решение:

Данная СЛУ однородна, то есть всегда имеет, по крайней мере, тривиальное решение.

.

Полученная матрица равносильна СЛУи имеет бесконечно много решений (ранг системы меньше числа неизвестных). Ранг системы 3, значит можно выразить три неизвестные через оставшуюся одну.

Обозначим x₄за параметри выразим остальные неизвестные через него (для удобства начнем записывать систему с последней строки):

Запишем столбец неизвестных в виде: , где– произвольное действительное число (R).

Обе записи равноправны и называются общим решением данной однородной системы.

Для того чтобы получить какое-либо частное решение достаточно подставить вместо параметра конкретное значение.

Например, – частное решение при=5.

Ответ: ,R.

5. Найти общее решение и какое-нибудь частное решение СЛУ

Решение:

Выполним «прямой ход» метода Гаусса для расширенной матрицы СЛУ:

.

Видим, что ранг основной матрицы равен рангу расширенной и равен 2, следовательно, система совместна. При этом в системе 4 неизвестных, следовательно, ранг меньше числа неизвестных, и система имеет бесконечно много решений. Полученная матрица равносильна СЛУ

Выполним «обратный ход» метода Гаусса. Ранг матрицы СЛУ равен 2, следовательно, можно выразить два неизвестных через остальные. Будем выражать x₁иx₂черезx₃,x₂(которые в этом случае называются свободными переменными). Обозначимx₃за параметр,x₄за параметр:



, ,R– общее решение.

Запишем частное решение при =1,=2:.

6. Найти общее решение и какое-нибудь частное решение СЛУ

Решение:

.

Исходная СЛУ равносильна Ранг системы 2, значение одной из переменных известно, осталось выразить одну неизвестную.

Общее решение СЛУ: или,,R.

Частное решение =3,=2:.

7. Решить систему и сравнить ее решение с решением соответствующей ей однородной системы.

Решение:

Однородная система, соответствующая данной получается из неоднородной системы заменой в ней свободных коэффициентов нулями. Решим сначала неоднородную СЛУ:



. Исходная СЛУ имеет бесконечно много решений и равносильна системе

Обозначим x₄за параметр и выразим все остальные неизвестные через него:



, R

Система будет решаться так же, как и неоднородная, но свободные члены при преобразованиях так и остаются нулями.

Общее решение однородной системы: ,R.

Решения неоднородной и соответствующей ей однородной систем отличаются только наличием столбца свободных членов, который является частным решением неоднородной системы.