§4. Обратная матрица

Основные определения по данному разделу можно прочесть на стр.18-20, ч. 1, [3]. Следует помнить, что только невырожденная матрица обратима.

Рассмотрим два основных метода поиска матрицы, обратной данной:

• Метод Гаусса. Процесс поиска обратной матрицы состоит в выполнении элементарных преобразований со строками расширенной матрицы (AE), переводящих эту матрицу в матрицу (EA^-1). Причем, преобразуются строки расширенной матрицы, то есть строки длинной 2n.

• Метод союзной матрицы. Применение формулы , гдеA* - матрица, союзная (присоединенная) кA.

1. Существует ли A^-1, если:.

Матрица Aвырождена (второй столбец нулевой) ине имеет обратной.

2. Обратима ли матрица ?

Матрица обратима, то есть имеет обратную, так какdet A= 10.

3. Найдите матрицу, обратную к .

Решение:

, значит, матрица обратима.

Воспользуемся методом Гаусса для поиска обратной матрицы. Запишем расширенную матрицу, состоящую из двух частей: слева запишем данную матрицу, справа единичную соответствующего порядка. При помощи элементарных преобразований над строками (всей расширенной матрицы) приведем эту матрицу к виду, когда слева будет стоять единичная матрица. Тогда матрица, которая получится справа, будет искомой обратной матрицей.





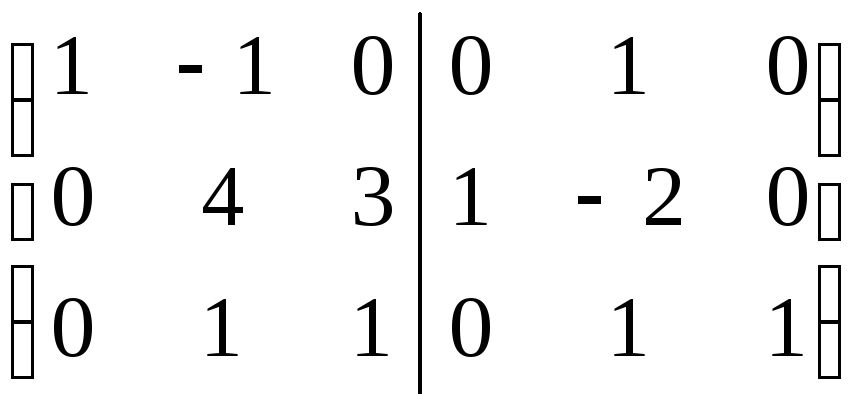
Для проверки воспользуемся равенством из определения обратной матрицы:

;

. A^-1=.

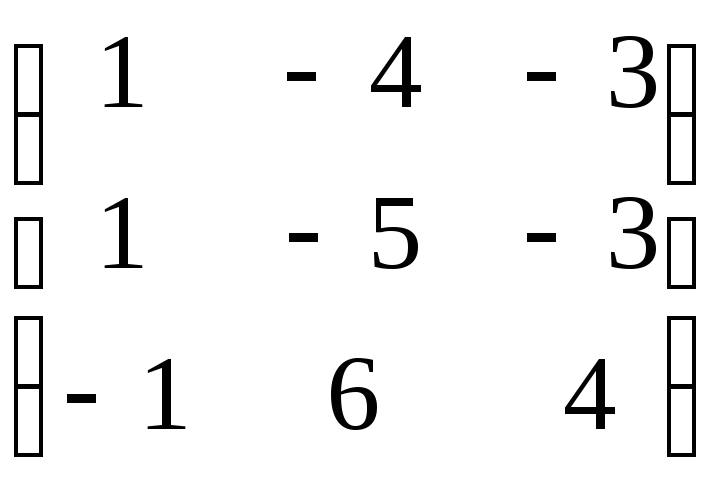4. Найдите матрицу, обратную к .

Решение:

, значит, данная матрица обратима. Заметим, что она уже имеет треугольный вид, то есть наша задача облегчается и нам необходимо провести только «обратный ход» метода Гаусса:



.

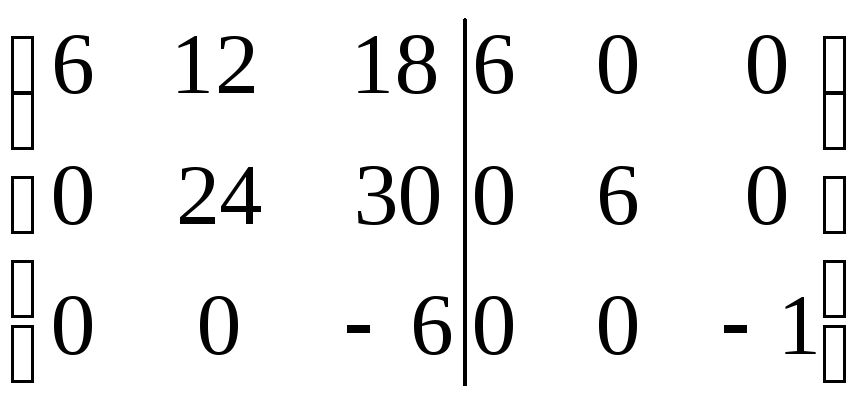
Проверка:

5. Найдите A^-1, если.

Решение:

Покажем применение метода союзной матрицы.

, то есть матрица Aобратима. Найдем алгебраические дополнения, используя равенство, связывающее их с минорами:

Составим из этих алгебраических дополнений матрицу, союзную к A:

.

Следовательно, .

Заметим, что если необходимо использовать обратную матрицу в дальнейшем для каких-либо вычислений, то лучше не вносить числовой множитель, записывать его перед всей матрицей.

Проверка:

=

=. Аналогично,A^-1A=E.

6. При каких aиbдля матрицаобратима?

Решение:

Матрица обратима, если ее определитель не равен нулю. Найдем условия, при которых это не так: 0. Для этого разложим левую часть на множители:

Итак, если b=-aилиb=2a, то определитель равен нулю и, следовательно, обратной матрицы не существует.

Ответ: обратная матрица существует, если

Глава 2. Системы линейных уравнений

Основные определения и утверждения по данному разделу можно прочесть на стр.22-30, ч.1, [3].

§1. Исследование на разрешимость систем линейных уравнений

Системы линейных уравнений (СЛУ) могут быть совместны, то есть разрешимы, и несовместны, то есть не иметь решений.

Для совместности СЛУ необходимо и достаточно, чтобы ранги основной и расширенной матриц совпадали (теорема Кронекера – Капелли).

Исследовать СЛУ – это значит решить вопрос совместности, и если она совместна, то указать число ее решений. Известно, что:

• если ранг совместной системы равен числу неизвестных, то система имеет одно решение;

• если ранг совместной системы меньше числа неизвестных, то она имеет бесконечно много решений.

1. Для запишите основную и расширенную матрицы. Запишите СЛУ в виде матричного уравнения.

Решение:

Основной матрицей СЛУ называется матрица коэффициентов при неизвестных, то есть . Расширенная матрица СЛУ – матрица вида, гдеA– основная матрица системы,b– столбец свободных членов СЛУ. Вертикальная черта проводится для визуального отделения левой и правой частей.

В нашем случае расширенная матрица: .

Левые части равенств СЛУ представляют собой суммы произведений элементов строк основной матрицы на неизвестные x₁,x₂,x₃. Следовательно, по определению произведения матриц, левую часть СЛУ можно записать в виде произведения основной матрицы на столбец, состоящий из неизвестных:. При умножении этих матриц получаем столбец, состоящий из трех элементов. По определению равенства матриц исходная СЛУ равносильна матричному уравнению:.

2. Для системы 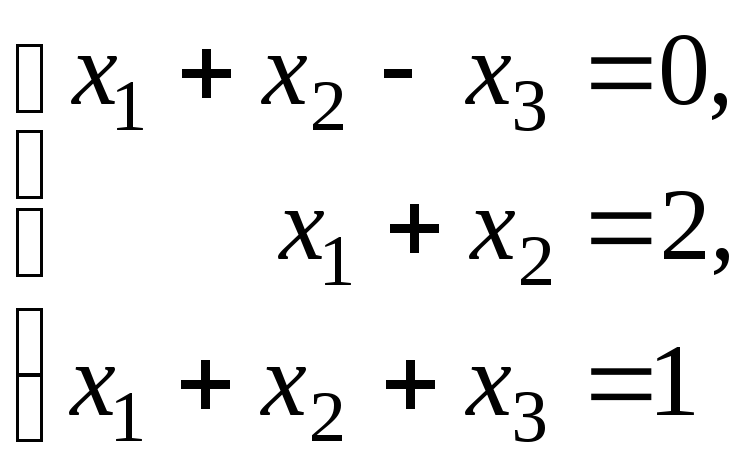запишите основную и расширенную матрицы. Запишите СЛУ в виде матричного уравнения.

Решение:

Если в каком-либо уравнении не участвует некоторая неизвестная, то соответствующий элемент в основной матрице будет равен нулю.

Основной матрицей СЛУ будет . Расширенная матрица:. Система может быть записана в виде:.

3. Исследовать на разрешимость систему:

Решение:

По теореме Кронекера – Капелли СЛУ совместна, если ранги ее основной и расширенной матриц равны. Для сравнения рангов СЛУ удобно пользоваться методом Гаусса приведения матриц к ступенчатому виду (подробно этот процесс рассматривался при поиске рангов матриц). При этом возможно появление строк вида . Если хотя бы одна такая строка появилась, то СЛУ несовместна. Это значит, что ранг расширенной матрицы больше ранга основной. Запишем расширенную матрицу СЛУ и приведем ее к ступенчатому виду:

. Видим, что ранг основной матрицы равен рангу расширенной и равен 3, следовательно, система совместна. При этом ранг совпадает с числом неизвестных, то есть СЛУ имеет единственное решение.

4. Исследовать на совместность систему

Решение:

Запишем расширенную матрицу и приведем ее к ступенчатому виду:

. Ранг расширенной матрицы равен рангу 3, а ранг основной матрицы равен 2, то есть СЛУ несовместна.

5. Исследовать на совместность СЛУ

Решение:

Система линейных уравнений, все свободные коэффициенты которой равны нулю, называется системой однородных линейных уравнений или однородной СЛУ. Однородные системы всегда разрешимы, так как имеют нулевое решение . Возникает вопрос: существуют ли еще решения, отличные от нулевого. Эти решения называются нетривиальными.

Проверим сколько решений имеет данная СЛУ, для этого ранг ее системы сравним с числом неизвестных.

.

Ранг матрицы равен 3, и он меньше числа неизвестных, которых 4, следовательно, система имеет бесконечно много решений.

6. Исследовать систему

Решение:

Запишем расширенную матрицу СЛУ и приведем ее к ступенчатому виду:



.

Ранг основной матрицы равен рангу расширенной и равен 3, то есть система совместна. При этом в системе 4 неизвестных, следовательно, ранг меньше числа неизвестных, и система имеет бесконечно много решений.