§3. Ранг матрицы

Основные определения и утверждения к этому разделу можно найти на стр.20-21, ч.1, [3]. Обозначения ранга матрицы A:rang A илиrg A.

Следует помнить, что ранг матрицы не изменяется при элементарных преобразованиях, к которым относятся:

• Перестановки строк (столбцов).

• Умножение строки (столбца) на число, не равное нулю.

• Сложение строк (столбцов).

• Вычеркивание нулевой строки (столбца).

Матрица, полученная при помощи элементарных преобразований, называется подобной данной. Приводим матрицу элементарными преобразованиями к ступенчатому виду с разным числом нулей в строках (в частном случае, к треугольному виду). Ранг такой матрицы равен количеству ненулевых ее строк. Тогда вопрос о ранге матрицы сводится к вопросу о строках подобной ей ступенчатой матрицы.

1. Сколько миноров второго порядка имеет матрица ? Выписать все эти миноры.

Решение:

Для того чтобы перечислить все миноры второго порядка в данной матрице, будем выделять по две произвольные строки и два произвольных столбца. Определители 2-го порядка, составленные из элементов матрицы A, расположенных на пересечении выделенных строк и столбцов, будут искомыми минорами 2-го порядка. Напомним, что матрица порядкаm×nимеетминоровk-го порядка, то есть в нашем случаеминоров второго порядка:

.

Мы выделяли сначала 1-ый и 2-ой столбцы, при этом 1-ю и 2-ю строки, потом 1-ю и 3-ю строки, потом 2-ю и 3-ю строки, далее поменяли выбор столбцов и рассмотрели те же наборы строк.

2. Найти ранг матрицы .

Решение:

Выбрав 1-ю и 3-ю строки, а так же 1-ый и 4-ый столбец, составим определитель из элементов матрицы A, расположенных на пересечении выделенных строк и столбцов:, следовательно,. Все миноры данной матрицы 3-го порядка равны нулю, поскольку в составлении минора участвует вторая нулевая строка. Значит, ранг матрицы равен 2.

При решении этой задачи можно использовать так же элементарные преобразования. Вычеркнув из матрицы 2-ю строку, а затем 2, 3 и 4-й столбцы, получаем матрицу , имеющую тот же ранг, что иA.

B= 22 – 15 = 70 .

3. Найти ранг матрицы .

Решение:

Все миноры второго, третьего и четвертого порядка матрицы равны нулю, так как элементы их строк пропорциональны. Миноры же первого порядка (сами элементы матрицы) отличны от нуля. Следовательно, .

4. Найти ранг матрицы .

Решение:

Вычисления ранга матрицы будем проводить с помощью метода Гаусса, приводя матрицу элементарными преобразованиями к ступенчатому виду.

= =

===

= =.

Мы привели данную матрицу к виду, когда ранг равен количеству ненулевых ее строк. Следовательно, rang A = 2.

5. Найти ранг матрицы .

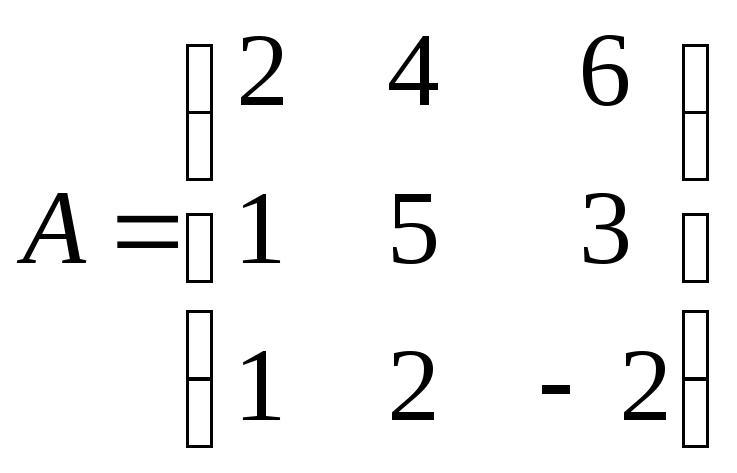Решение:

Приведем данную матрицу к ступенчатому виду элементарными преобразованиями:

= ==

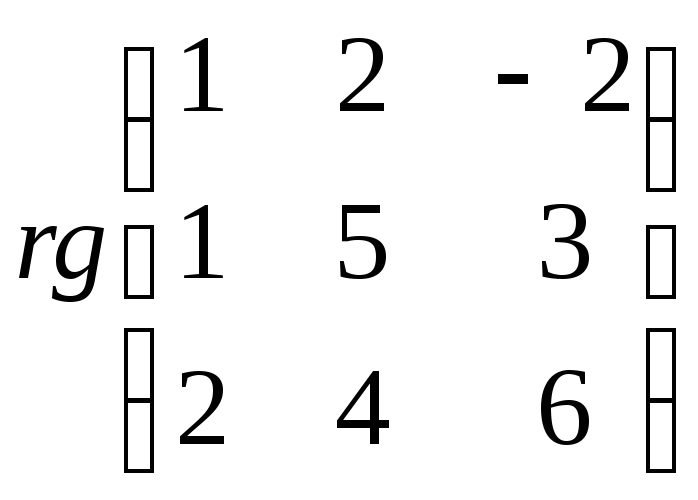===3.

6. Найти ранг при разных значенияхa.

Решение:

Хочется обратить внимание, что при применении элементарных преобразований, получаются подобные матрицы, а не равные. Поэтому нельзя между ними ставить знак равенства, можно использовать знак подобия «».

При помощи элементарных преобразований приведем данную матрицу к ступенчатому виду:



. Поясним выполненные нами действия:

1) вычтем из 2-й строки удвоенную 1-ю строку, вычтем из 3-й строки 1-ю;

2) вычтем из третьей строки удвоенную вторую.

Видим, что в полученной ступенчатой матрице при a=3 последняя строка становится нулевой, в остальных случаях это не так.

Ответ: rang B = 2 при a=3, rang B = 3 при a3.