2. Решение типовых задач

Задача 1.1. Составить уравнение плоскости, проходящей через точку

,если задан нормальный вектор.

Р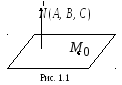ешение.Воспользуемся уравнением (1.2):

Подставляя координаты вектора и точки, получим

Ответ:

Задача 1.2. Составить уравнение плоскости, проходящей через точкупараллельно векторами(их называют направляющими векторами плоскости).

Решение.

П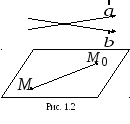ервый способ.Пусть– ­произвольная точка на плоскости.Тогда векторы и(рис. 1.2) должны быть компланарны, т. е. их смешанное произведение должно быть равно 0:.Запишем смешанное произведение через координаты векторов. Получим

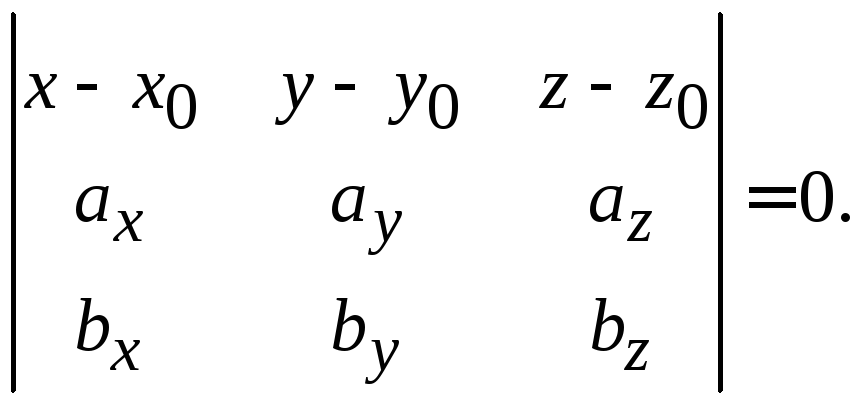
Подставим заданные координаты и вычислим определитель разложением по элементам первой строки:

,

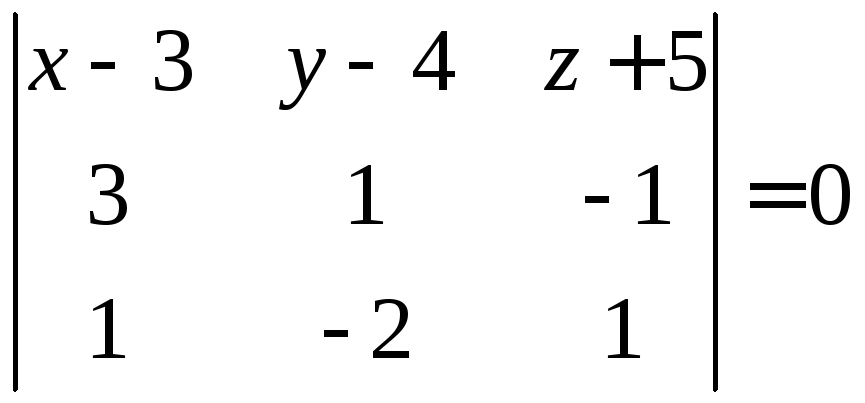или

.

Окончательно:

Второй способ. Найдем сначала вектор(рис. 1.1). Очевидно, что вектор нормали к плоскости должен быть ортогонален также векторами. Поэтому его можно выбрать как векторное произведение

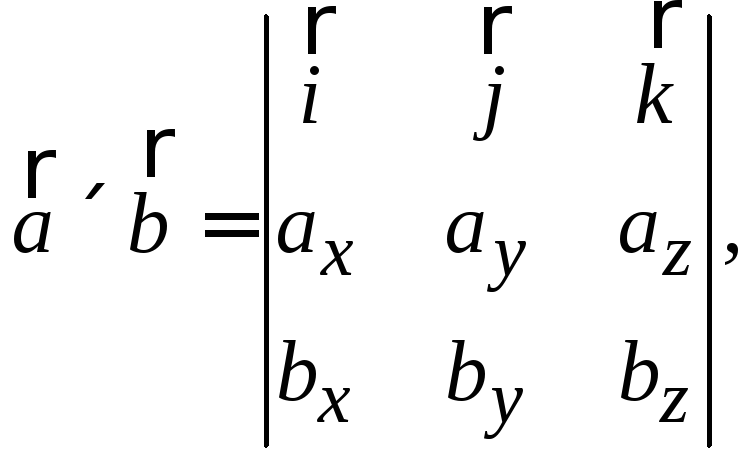
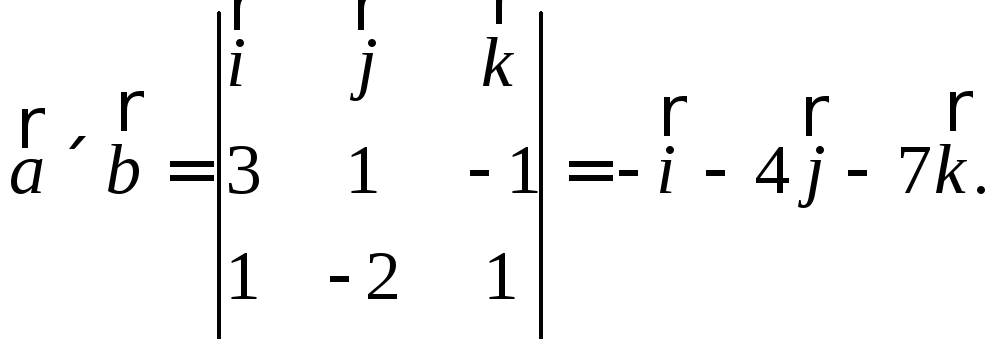
Затем выпишем общее уравнение плоскости, используя ,(см. формулу (1.2)). Получим

Ответ:

Полезная формула. Если плоскость проходит через точку , и– ее направляющие векторы, то уравнение плоскости имеет вид

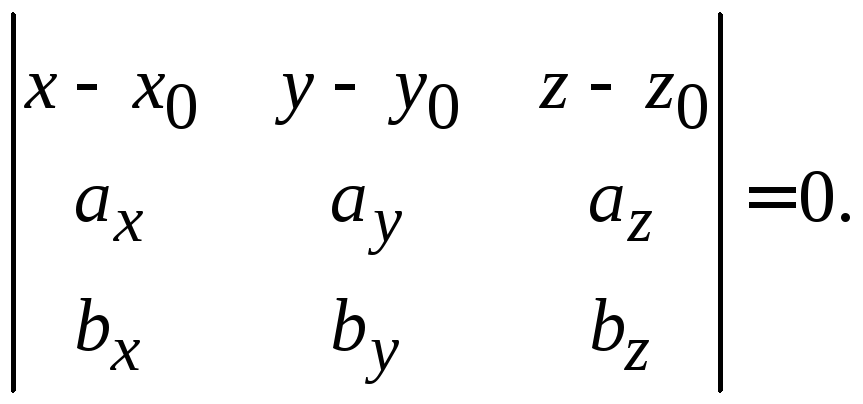(1.7)

Замечание.Первый способ решения задачи предпочтительнее. Второй способ отличается лишь тем, что в нем смешанное произведение трех векторов,,вычисляется последовательно. А именно: сначала находим векторное произведениеи затем результат умножаем скалярно на вектор. В дальнейшем при решении задач будем придерживаться первого способа.

Задача 1.3. Составить уравнение плоскости, проходящей через точкиипараллельно вектору.

Р

ешение.Пусть произвольная точка на плоскости. Тогда векторы,икомпланарны (рис. 1.3). Запишем условие компланарности векторов через их координаты:

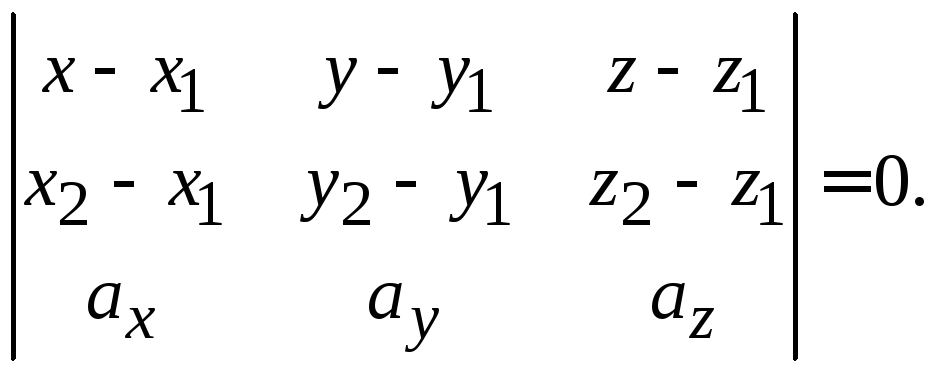
Подставляя заданные координаты, получим

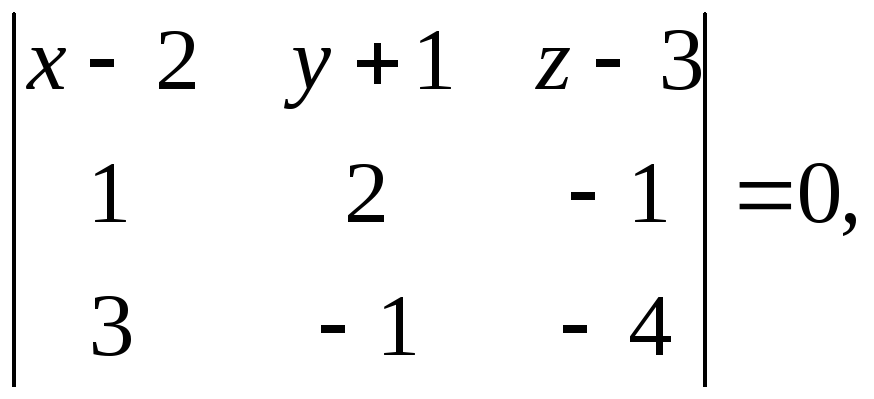
или

Окончательно:

Ответ:

Полезная формула.Если плоскость проходит через две заданные точкиипараллельно вектору, то ее уравнение имеет вид

(1.8)

Задача 1.4. Составить уравнение плоскости, проходящей через точкупараллельно плоскости

Решение. В качестве вектораискомой плоскости можно выбрать нормальный вектор заданной плоскости, так как эти плоскости параллельны. Таким образом, имееми. Подставляя координатыив уравнение (1.2), получим

Окончательно:

Ответ:

Задача 1.5. Найти величину острого угла между плоскостямии

Решение. Угол между плоскостями равен углу между нормальными векторамии(см. формулу 1.4)).

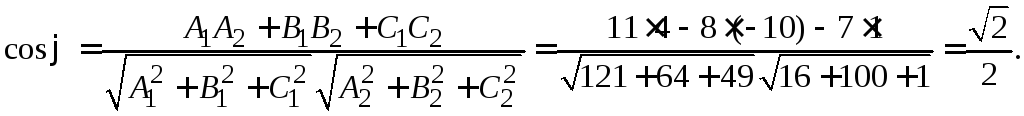
Отсюда

Ответ:

Задача 1.6. Чему равен угол между плоскостямии?

Решение. Найдем скалярное произведение нормальных векторов и

Следовательно, эти плоскости перпендикулярны:

Ответ:

Задача 1.7. Составить уравнение плоскостей, которые проходят через точкуи отсекают на координатных осях отличные от нуля отрезки одинаковой длины.

Р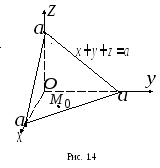ешение.Воспользуемся уравнением плоскости в отрезках на осях (1.3). Рассмотрим сначала случай 1:(рис. 1.4). Тогда получим

Подставляя в уравнение координаты точки , найдем

Уравнение плоскости: Затем следует аналогично рассмотреть случаи 2: 3: 4: Получим четыре различные плоскости.

Ответ:

Задача 1.8. Построить плоскости, заданные уравнениями: 1);2) ; 3) ; 4) плоскость, проходящую через точкупараллельно плоскости; 5) плоскость, проходящую через точкуи ось.

Р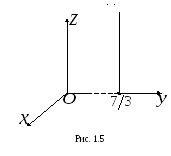ешение.1. Плоскостьпараллельна плоскостии отсекает на осиотрезок, равный (рис. 1.5).

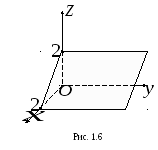
2. Плоскость параллельна оси, пересекает плоскость по прямой , отсекая на осяхиотрезки, равные 2 (рис. 1.6).

3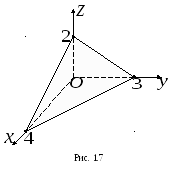. Уравнение плоскости запишем в отрезках на осях (1.3):. Плоскость отсекает на осях,,отрезки, длины которых равны соответственно 4, 3, 2 (рис. 1.7).

Рис. 1.8

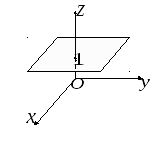
4. Так как плоскость параллельна плоскости, то ее нормальный вектор можно выбрать в виде. Тогда согласно формуле (1.2) уравнение плоскостибудет, гдепо условию задачи. Таким образом, получаем(рис. 1.8).

5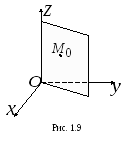. Плоскостьпроходит через ось. Поэтому ее нормальный вектор имеет вид. Так как плоскость проходит через начало координат, то коэффициент в уравнении плоскости (1.1) равен 0. Подставляя координаты точки в уравнение, получаем(рис. 1.9).

Задача 1.9. Составить уравнение плоскости, проходящей через три заданные точки

Р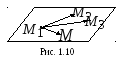ешение.Пусть произвольная точка на плоскости. Тогда векторы,,компланарны (рис. 1.10). Запишем условие компланарности этих векторов через их координаты:

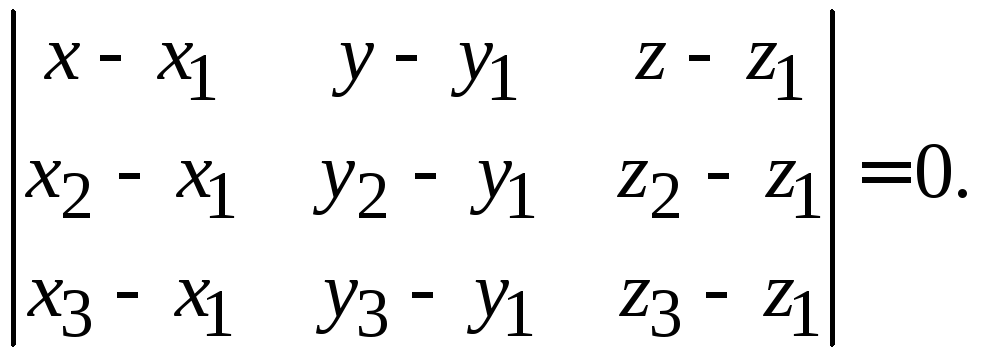Подставим значения координат и найдем уравнение плоскости:

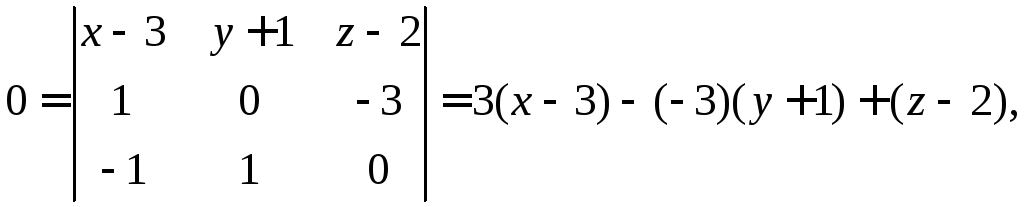
или

Ответ:

Полезная формула. Если плоскость проходит через три заданные точкине лежащие на одной прямой, то ее уравнение имеет вид

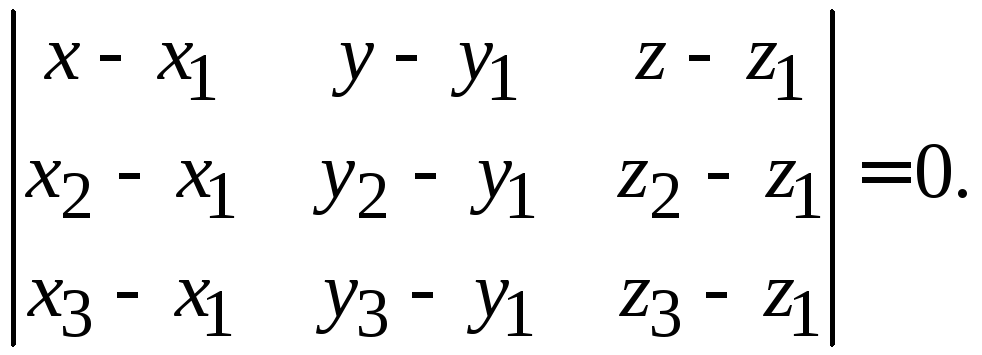(1.9)

Задача 1.10. Даны координаты вершин тетраэдра: ,,,(рис. 1.11). Составить уравнения его граней.

Р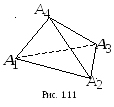ешение.Найдем уравнение грани. Для этого подставим в формулу (1.9) координаты вершин:

,

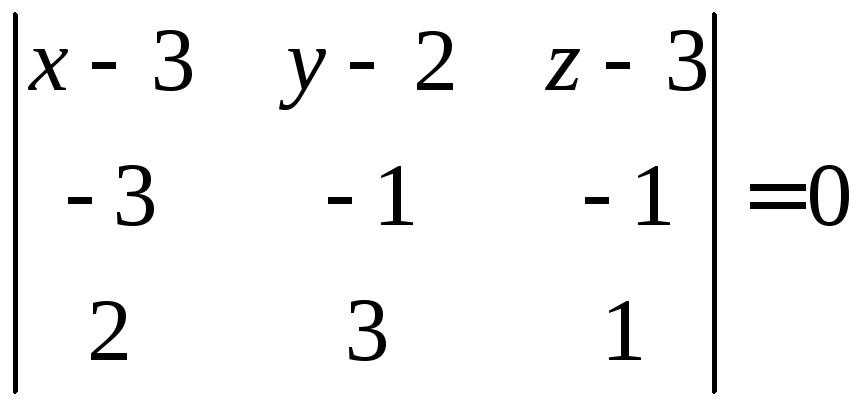или

.

Уравнение искомой грани имеет вид

Уравнения граней ,,найдите самостоятельно.

Ответ:

.

Задача 1.11. Найти расстояние от точкидо плоскости

Решение. Используем формулу (1.5):.

Ответ:

Задача 1.12. Найти расстояние между параллельными плоскостями

.

Решение.

Первый способ. Выберем произвольно точку на плоскости . Пусть, например,ТогдаСледовательно,Найдем расстояниеот точкидо плоскости, по формуле (1.5):

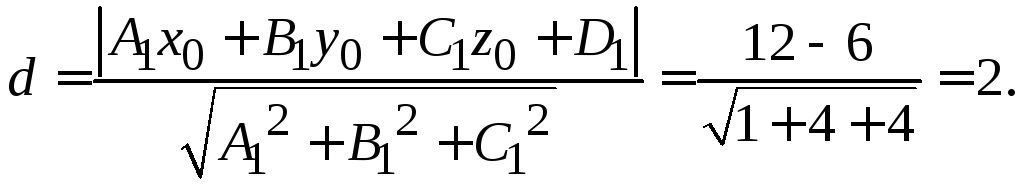
В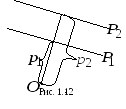торой способ.Очевидно, что плоскостиилежат по одну сторону относительно начала координат

Обозначим через расстояние от начала координат до плоскости, через– до плоскости(рис. 1.12).

,

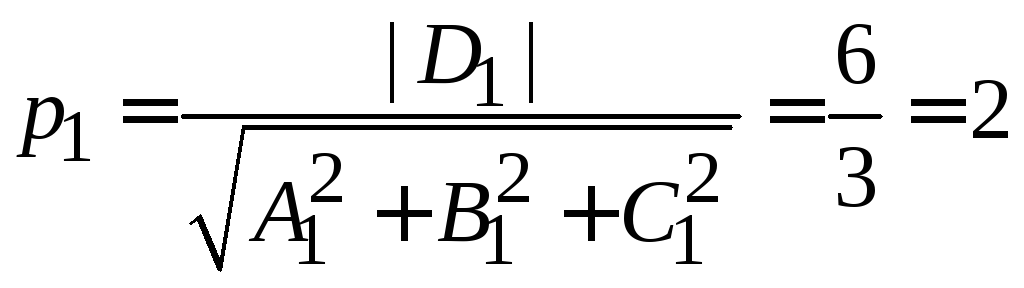
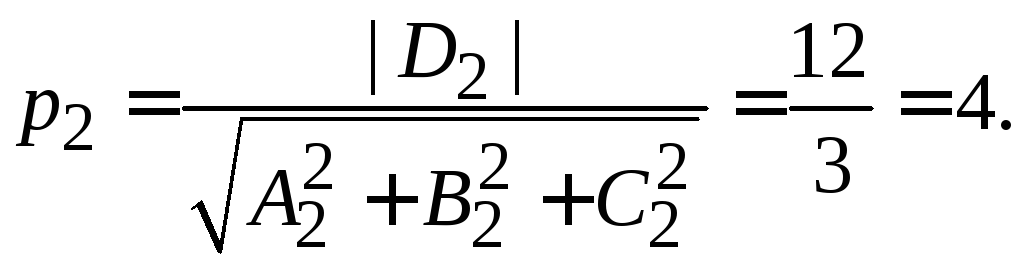
Расстояние между плоскостями равно . Отсюда находим

Ответ:

Замечание. Если бы плоскости находились по разные стороны от начала координат (рис. 1.13), то расстояние между ними было бы равно

Задача 1.13. Составить уравнение плоскости, проходящей через заданную прямуюи точкуне лежащую на этой прямой.

Решение. Уравнение произвольной плоскости, проходящей через заданную прямую, имеет вид (см. формулу (1.6))

Отсюда

:

Подставляя в это уравнение координаты точки , получим

,

Положим, например, ТогдаОстается подставить эти коэффициенты в уравнение плоскости. Получим

Ответ:

Задача 1.14. Написать уравнение биссектрисыострого двугранного угла между плоскостямии

Решение. Нормальные векторы первой и второй плоскостей соответственно равны иОни образуют острый угол, так как

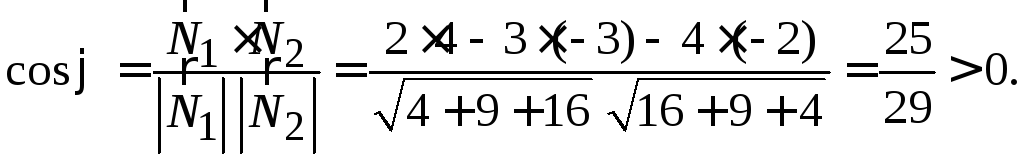
Очевидно, что (Нормальные векторыивсегда можно взять равными по длине, например, единичными.) Так как, то параллелограмм, построенный на векторахикак на сторонах, является ромбом, а диагональбиссектрисой его угла. Следовательно, векторможет быть выбран в качестве нормального вектора искомой биссектрисыДалее следуем рассуждениям задачи 1.13. Уравнение биссектрисыищем в виде

Отсюда

Учитывая, что получаем систему уравнений

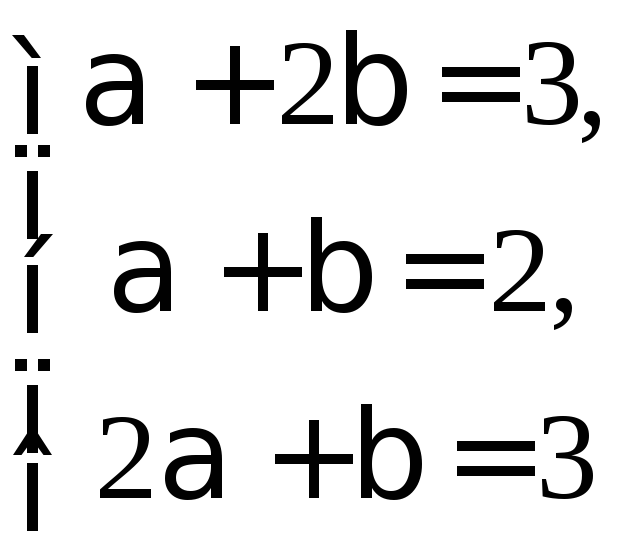
Подставляя эти значения в уравнение биссектрисы , имеем

Окончательно:

Чертеж к этой задаче предлагаем сделать самостоятельно.

Ответ: