ДУ-6 ЛДУ-1-2 с пост коэфф Системы ЛДУ-1

5

§6 Операционный метод решения задачи Коши для систем ЛДУ-1 с постоянными коэффициентами.

Определение. Задачу Коши для ЛДУ-1 и системы «n» ЛДУ-1 c постоянными коэффициентами сформулируем так:

Систему [*] запишем в матричном виде:

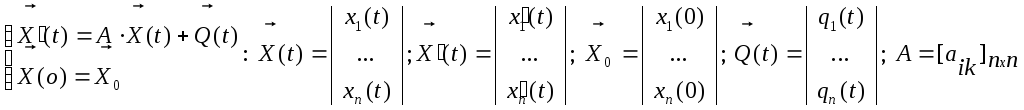
Если функции - оригиналы, после преобразования Лапласа задача Коши для системы ЛДУ-1 отобразится в СЛАУ относительно изображения решения з. Коши . Обратное преобразование Лапласа восстанавливает решение задачи Коши

Пример.

Замечание. Очевидно, что аналогично операционным методом решается задача Коши для ЛДУ-n с постоянными коэффициентами и n начальными условиями: x^(k)(0)=x_K.

===========================================

ИДЗ-2 (ТР-2.9) по теме «Системы ЛДУ-1 и ЛДУ-2 с постоянными коэффициентами» Максимум = 10 баллов. Зачет ≥ 7 баллов.

Задание.

[0] Используемые теоремы операционного исчисления = 2б.

1. Операционным методом решить задачу Коши для заданных систем (1,2) ЛДУ первого порядка с постоянными коэффициентами. 2б.+ 3б.

2. Операционным методом решить задачу Коши для ЛДУ второго порядка с постоянными коэффициентами. 3б.

Пример выполнения ИДЗ-2.

1. (1)

где:

Преобразование Лапласа отображает систему ЛДУ (1) в СЛАУ относительно

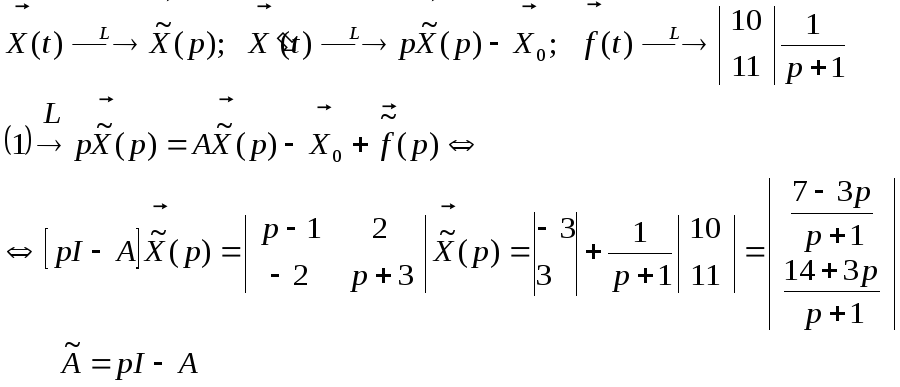По формулам Крамера

3.

Запишем аналитический вид правой части ЛДУ-2:

После преобразований Лапласа получим алгебраическое уравнение относительно :

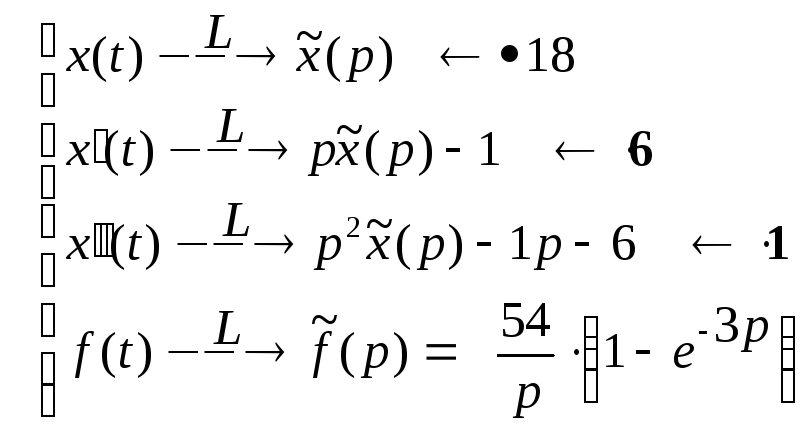
Решение задачи Коши восстановим обратным преобразованием Лапласа с учетом т. смещения и запаздывания.

Результат.

Вариант-2 для задачи 3.