
- •Дифференциальное Исчисление Функций Нескольких Переменных [дифнп].
- •§2 Функции Нескольких Переменных (фнп). 4
- •§2 Функции Нескольких Переменных (фнп).
- •§3. Предел и непрерывность фнп.
- •§4.Частные производные фнп. Производная и градиент фнп.
- •§5 Формула и полином Тейлора 1 порядка.
- •§ 7 Производная фнп по направлению. Свойства градиента фнп.
- •§8 Частные производные второго порядка. Матрица Гессе. Формула Тейлора 2 порядка
- •§9 Локальные экстремумы фнп. Необходимый признак л.Э.
- •§10. Достаточное условие локального экстремума фнп.
§5 Формула и полином Тейлора 1 порядка.
Из ДИФОП:
-

Пусть ![]() и в т.
и в т.
![]() существует
существует
![]()
Утверждение.
Если
в точке
![]() функция f
дифференцируема в точке а
и при
функция f
дифференцируема в точке а
и при
![]() имеет место формула Тейлора 1 порядка
имеет место формула Тейлора 1 порядка

![]()
Следствие.
При
![]() значения функции
значения функции
![]() в
окрестности точки дифференцируемости
отличаются от значений ее полинома
Тейлора
в
окрестности точки дифференцируемости
отличаются от значений ее полинома
Тейлора
![]() на
бесконечно малую более высокого порядка
малости чем
на
бесконечно малую более высокого порядка
малости чем
![]()
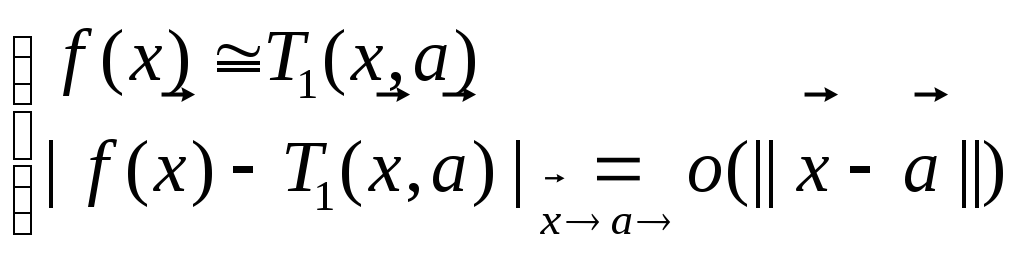
Пример.
Вычислим приближенное
значение f(x,y)=xexy
в точке ![]()
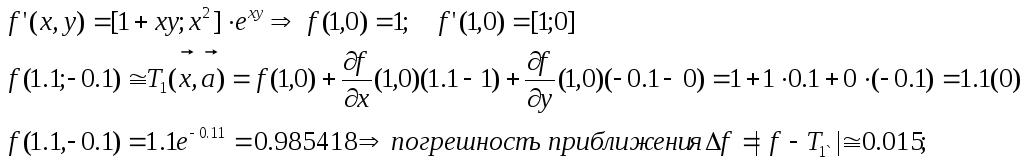
ЭКЗ: Вычислить
приближенное значение
![]() ,
если f(x,y,z)=x∙y∙ex∙z
,
если f(x,y,z)=x∙y∙ex∙z
§ 6 Касательная плоскость и нормаль к гладкой поверхности z=f(x,y).
Из Аналитической Геометрии…
![]()
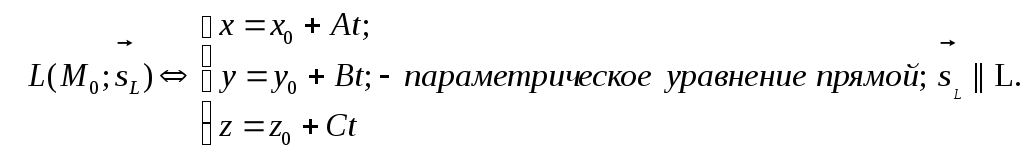
---------------------------------------------------------------------
Пусть точка M0(x0,y0,z0=f(x0,y0)) – точка гладкой поверхности z=f(x,y).
Рассмотрим уравнение ![]() ,
,
которое определяет в R3 плоскость - «график» полинома Тейлора.
Определения.
Плоскость, проходящая через точку М0(x0,y0,z0=f(x0,y0)) гладкой поверхности z=f(x,y)
![]()
называется касательной плоскостью к поверхности z=f(x,y) в точке М0.
Прямая
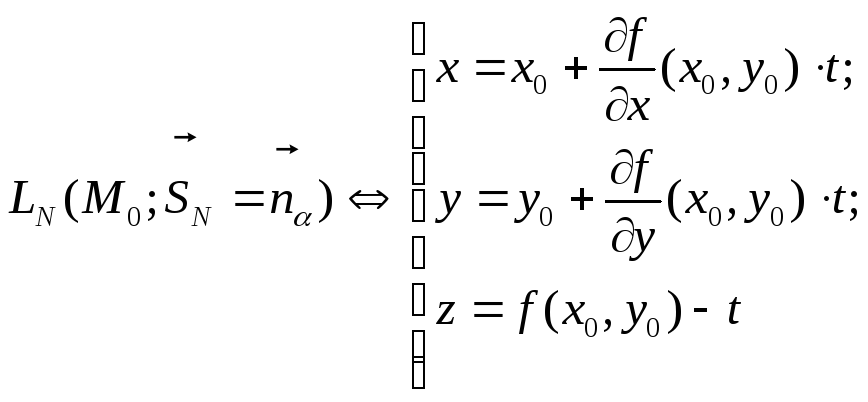 проходящая через точку
М0
поверхности и перпендикулярная
касательной плоскости, называется
нормалью к поверхности
в точке М0.
проходящая через точку
М0
поверхности и перпендикулярная
касательной плоскости, называется
нормалью к поверхности
в точке М0.
Пример.
Запишем уравнения
касательной плоскости αКАС
и нормали LN
к гладкой поверхности
z=xexy
в точке M0(1,2,e2):
![]()
![]() e2[1+3(x-1)+(y-2)]
e2[1+3(x-1)+(y-2)]
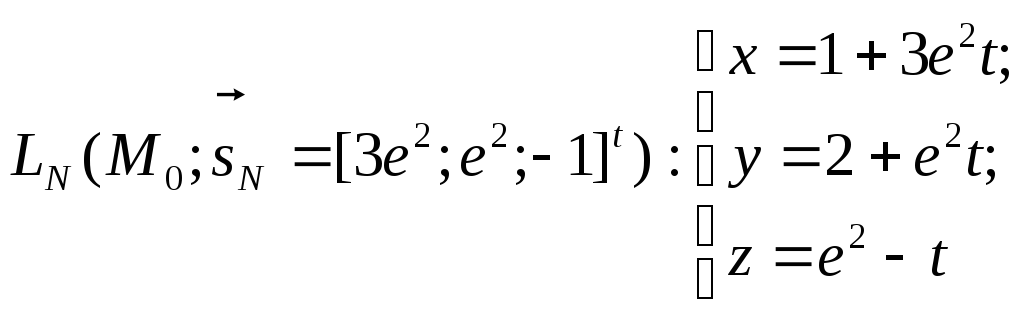 .
.
Важное соглашение!
В дальнейшем будем отождествлять следующие утверждения :
f дифференцируема в точке a€Rn в окрестности точки a имеет место формула Тейлора первого порядка
![]()
в
точке a
существуют все частные производные
![]()
в точке A(a,f(a)) существует касательная плоскость и нормаль к гладкой поверхности z=f(x,y).
ЭКЗ: Записать уравнения касательной плоскости и нормали к поверхности z= arcsin(x/y) в точке A(1,2,π/6)
§ 7 Производная фнп по направлению. Свойства градиента фнп.
Пусть ФНП f
дифференцируема в точке а![]() и задан вектор
и задан вектор ![]()
![]()
![]()
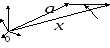 ,
определяющий в Df
некоторое направление.
,
определяющий в Df
некоторое направление.
![]()
Запишем для точки ![]() формулу Тейлора 1 порядка:
формулу Тейлора 1 порядка:
![]()
Определение. Производной функции f в точке а в направлении r называется число
![]() ,
,
равное скалярному произведению градиента функции в точке на единичный вектор направления.
Замечания.
1.
Модуль
![]() определяет «скорость
изменения»
функции в точке
определяет «скорость
изменения»
функции в точке
![]() в направлении
в направлении
![]() , а «знак»
, а «знак»
![]() -
возрастание или убывание функции f
в точке
-
возрастание или убывание функции f
в точке
![]() в заданном направлении :
в заданном направлении :
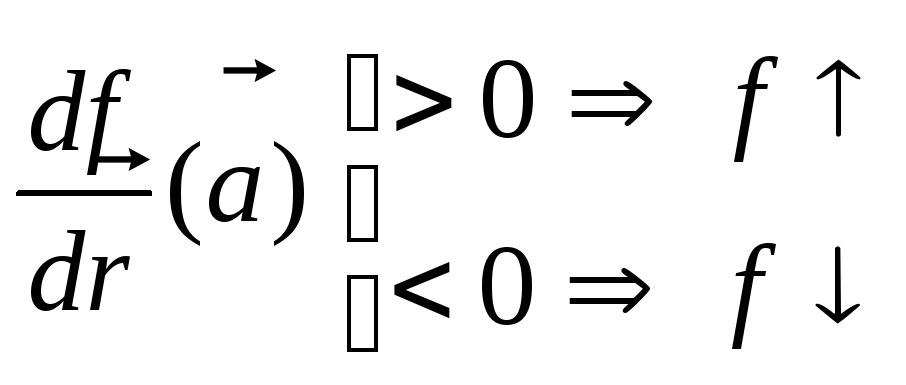
2.
Из свойств скалярного произведения
векторов
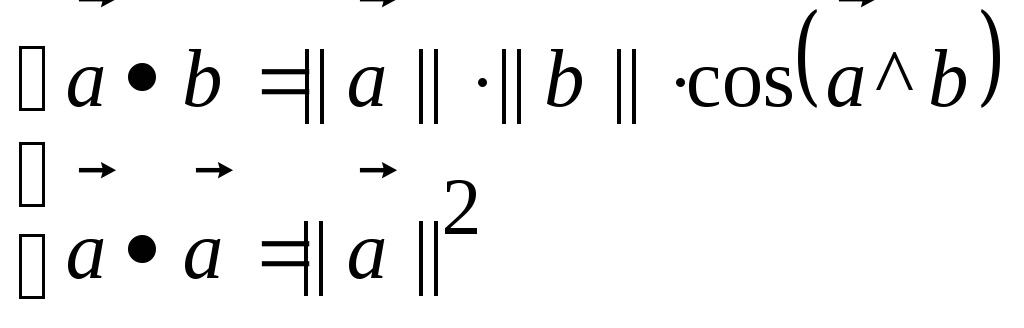 следует, что функция f
с наибольшей
скоростью
Vmax=|grad
f(a)|
возрастает
в
направлении
следует, что функция f
с наибольшей
скоростью
Vmax=|grad
f(a)|
возрастает
в
направлении
![]() и убывает
в направлении
и убывает
в направлении
![]() .
.
Пример. f(x,y)=xexy; a=[1;2]t; r=[1;1]t. Найти в точке a производную функции f по направлению r
gradf(a)=e2[3;1]t;
![]()
ЭКЗ. Найти в точке А(1,2,3) производную функции g(x,y,z)= x2y - xy2 +2xyz2 в направлении радиус-вектора точки А.
§8 Частные производные второго порядка. Матрица Гессе. Формула Тейлора 2 порядка
Для функции ”n”
переменных ![]() ,
непрерывной в точке
,
непрерывной в точке ![]() ,
определены ”n”
(первых)
частных производных функций ”n”
переменных :
,
определены ”n”
(первых)
частных производных функций ”n”
переменных : ![]() .
Если функция
.
Если функция ![]() непрерывна в точке
непрерывна в точке ![]() ,
для нее аналогично определены ”n”
,
для нее аналогично определены ”n”
ее частных производных, которые называют вторыми частными производными функции f. Очевидно, что для функции ”n” переменных определены ”n2” вторых частных производных.
Определение.
Введем следующие определения и обозначения для вторых частных производных.
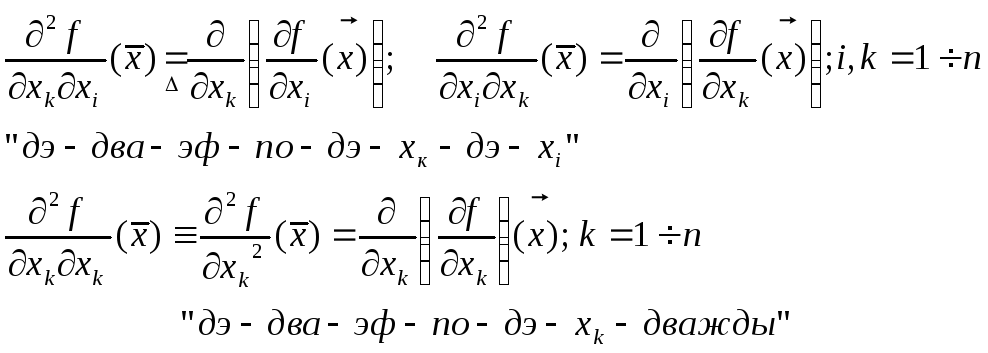
Квадратная матрица, составленная из вторых частных производных, называется
Матрицей Гессе.
Например, для функции
f(x,y)=x2y3
![]()
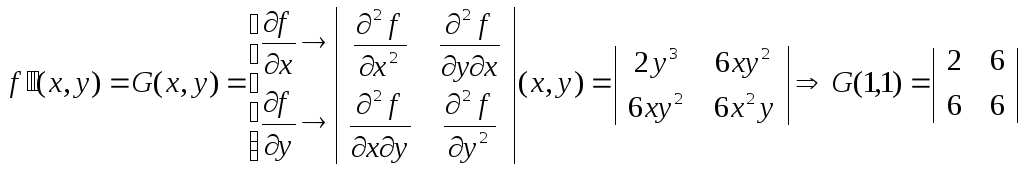
Утверждение.
Если вторые частные
производные функции f
непрерывны в точке
![]() ,
1)
«смешанные»
частные производные не зависят от
порядка дифференцирования
,
1)
«смешанные»
частные производные не зависят от
порядка дифференцирования
![]() и
матрица
Гессе G(
и
матрица
Гессе G(![]() )является
симметричной
;
2)
в
окрестности точки дифференцируемости
имеет место формула
Тейлора второго порядка
)является
симметричной
;
2)
в
окрестности точки дифференцируемости
имеет место формула
Тейлора второго порядка
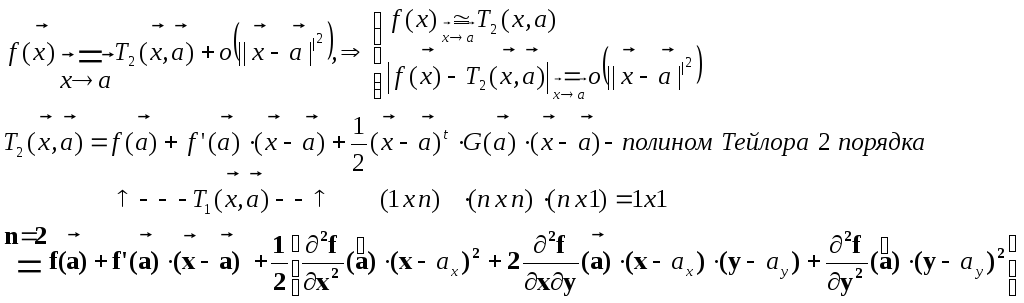
Пример. Сравним значения функции и её полиномов Тейлора 1-го и 2-го порядков в окрестности точки дифференцируемости.
f(x,y)=x2y3; x=(1.1;0.9); a=(1;1)
f(x )=1.12∙0.93=0.88209; T1(x,a)= 1+2∙0.1-3∙0.1 =0.9(0); T2(x,a)= 0.9 + 0.5(2∙0.12-2∙6∙0.1∙0.1+6∙0.12) =0.88(0)
|f(x) – T1(x,a)|≈2∙10-2; |f(x) - T2(x,a)|≈2∙10-3
==========================================================
ЭКЗ: Сравнить для f(x,y)=yx значение 0.982.01 и значения соответствующих полиномов Тейлора 1-го и 2-го порядков.
