
- •Дифференциальное Исчисление Функций Нескольких Переменных [дифнп].
- •§2 Функции Нескольких Переменных (фнп). 4
- •§2 Функции Нескольких Переменных (фнп).
- •§3. Предел и непрерывность фнп.
- •§4.Частные производные фнп. Производная и градиент фнп.
- •§5 Формула и полином Тейлора 1 порядка.
- •§ 7 Производная фнп по направлению. Свойства градиента фнп.
- •§8 Частные производные второго порядка. Матрица Гессе. Формула Тейлора 2 порядка
- •§9 Локальные экстремумы фнп. Необходимый признак л.Э.
- •§10. Достаточное условие локального экстремума фнп.
Дополнительные главы математики. 3 семестр ОФ. 3 ч/нед. Дифф. Зачет. [I] ДИ ФНП – 32 час; СР «ФНП»; ТР 2.5 «ЛЭ f(x,y)»
[II] Функции Бесселя – 11 час. Дифф. зачет
[III] Комбинаторика – 8 час. Дифф. Зачет
Дифференциальное Исчисление Функций Нескольких Переменных [дифнп].
Основная литература.
Бугров Я.Н., Никольский С.М. Высшая математика, т.2: Дифференциальное и интегральное исчисление. Учебник для ВУЗов.-М.: Наука, 2003, 2005, 2007.
Сборник задач по математике для втузов. Учебное пособие для втузов, ч.2/ Под ред. Ефимова А.В. и Поспелова А.С.-М.: Физматлит, 2003.
Боревич Е.З., Жукова Е.Е., Челкак С.И. Дифференциальное исчисление функций многих вещественных переменных. Учебное пособие. – СПбГЭТУ «ЛЭТИ», 2001.
Колбина С.А. и др. Типовые расчеты по дисциплине «Математический анализ»: Учебное пособие. – СПбГЭТУ «ЛЭТИ», 2008.
Дифференциальное Исчисление Функций Нескольких Переменных [ДИФНП]. 1
§2 Функции Нескольких Переменных (фнп). 4
§3. Предел и непрерывность ФНП. 8
§4.Частные производные ФНП. Производная и градиент ФНП. 9
§5 Формула и полином Тейлора 1 порядка. 11
§ 6 Касательная плоскость и нормаль к гладкой поверхности z=f(x,y). 12
§ 7 Производная ФНП по направлению. Свойства градиента ФНП. 13
§8 Частные производные второго порядка. Матрица Гессе. Формула Тейлора 2 порядка 14
§9 Локальные экстремумы ФНП. Необходимый признак Л.Э. 15
§10. Достаточное условие локального экстремума ФНП. 16
Экз. задачи.
1. Изобразить на плоскости Df для функций:
![]()
2. Какие поверхности в R3 задаются уравнениями:
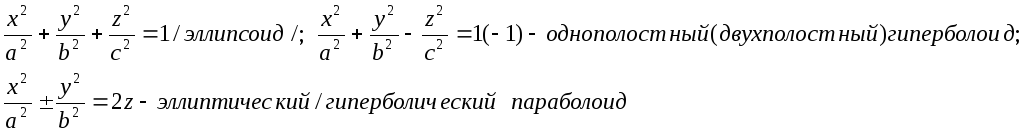
3.
Определить
композиции функций
![]() и
и![]() :
(1)
:
(1)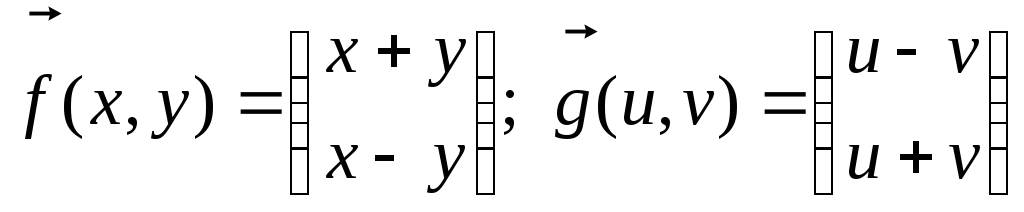 (2)
(2)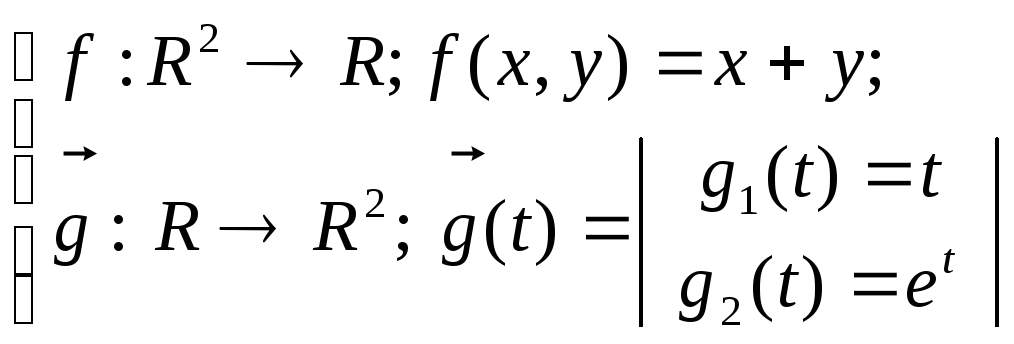
4. Найти
![]()
5) Показать,
что
![]()
6)
Вычислить
приближенное значение
![]() ,
если
f(x,y,z)=x∙y∙ex∙z
,
если
f(x,y,z)=x∙y∙ex∙z
7) Найти в точке А(1,2,3) производную функции g(x,y,z)= x2y - xy2 +2xyz2 в направлении радиус-вектора точки А.
8)
Найти
Л.Э. функции
![]()
§1. Введение. Основные понятия и определения. Из курсов АиГ и МА:
1)
Будем отождествлять: вектор
![]() и
точку
и
точку
![]() в n-мерном координатном
пространстве OX1X2…Xn,
норму вектора
в n-мерном координатном
пространстве OX1X2…Xn,
норму вектора
![]() и рачсстояние между точками
и рачсстояние между точками![]() .
.
2)
Окрестность и Проколотая
Окрестность радиусом r>0
точки
![]()
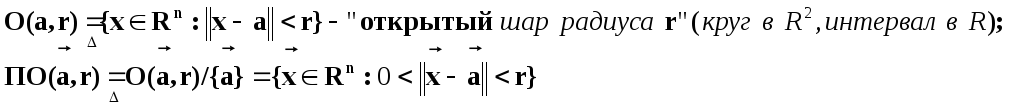
Следствия.
![]()
3) «Предельная
точка множества D![]() »
»
![]()
![]() -
любая
проколотая окрестность точки содержит
точки множества.
SOS:
-
любая
проколотая окрестность точки содержит
точки множества.
SOS:
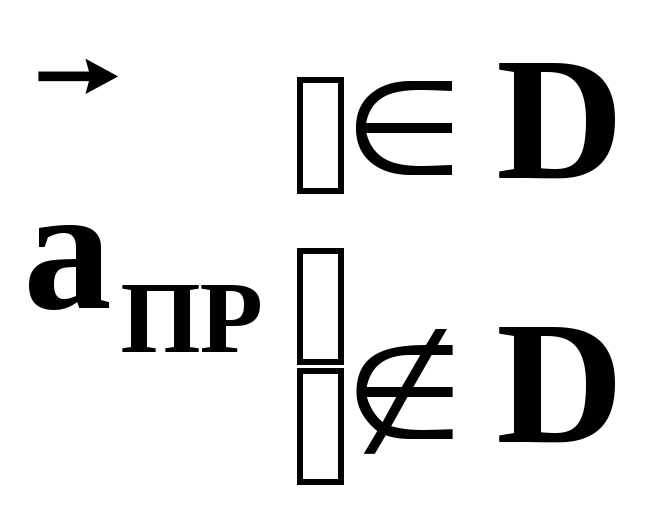
«Изолированная точка
множества D![]() »
»![]()
![]() -
некоторая
проколотая окрестность точки не содержит
точек множества.
-
некоторая
проколотая окрестность точки не содержит
точек множества.
«Внутренняя точка
множества D![]() »
»
![]() -«достаточно
малая» окрестность точки содержит
только точки множества. Любая
внутренняя точка множества является
его предельной точкой.
-«достаточно
малая» окрестность точки содержит
только точки множества. Любая
внутренняя точка множества является
его предельной точкой.
«Граничная
точка множества D![]() »
»
![]()
![]() -
либо
изолированная точка, либо точка, любая
окрестность которой содержит как точки
множества, так и точки, не принадлежащие
множеству.
-
либо
изолированная точка, либо точка, любая
окрестность которой содержит как точки
множества, так и точки, не принадлежащие
множеству.
«Граница
γD
множества D![]() »
»
![]() -
множество граничных точек множества.
-
множество граничных точек множества.
4) Множество D![]() называется
областью,
если все его точки –
внутренние.
Область
называется
областью,
если все его точки –
внутренние.
Область
![]() называется
замкнутой областью.
называется
замкнутой областью.

5) Линии на плоскости.
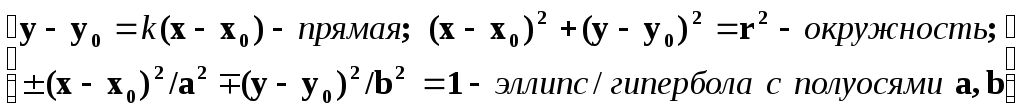
6) Алгоритм «метода интервалов» решения неравенств F(x,y) <(>) 0 для непрерывной функции.
(1) «Выколоть» на плоскости точки и линии, в которых функция не определена.
(2) Решить уравнение f(x,y)=0 и изобразить соответствующие «нулевые решения» - точки и линии «нулевого уровня» функции на плоскости.
(3)Определить «знак» функции в каждой части плоскости, ограниченной смежными «нулевыми линиями»,- вычислив значение функции в какой-нибудь внутренней точке.
(4) «Записать» множество решений неравенства.
Пример. Решить неравенство f(x,y)=|x/y| -1<0.
(1)![]()
“выколоть” на плоскости прямую L1:
y(x)≡0 .
“выколоть” на плоскости прямую L1:
y(x)≡0 .
(2) Уравнение f(x,y)=0|x/y|=1 |x|=|y| L1,2 : y=±x, f(L2,3 )=0
( 3)
3)![]()
A2(1,1/2);
D2
А6(-1,1/2)
А5(-1,-1/2) А3(1,-1/2)
D5 D3
D4
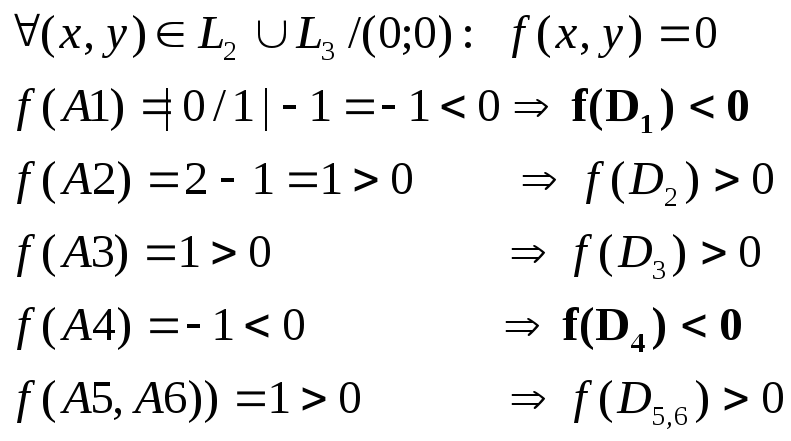 (4)
(4)![]()
