
- •Исследование линейных систем в среде matlab/simulink
- •Утверждено
- •Предисловие
- •Лабораторная работа №1 исследование динамических свойств типовых звеньев сау во временной и частотной областях
- •Основные сведения
- •1.2. Программа работы
- •1.3. Содержание отчета
- •Контрольные вопросы
- •Влияние параметров на качество автоматических систем
- •2.1. Основные сведения
- •2.2. Программа работы
- •2.2.1. Исследование влияния контурного коэффициента усиления системы на ее динамические свойства
- •2.2.2. Исследование влияния относительной инерционности звеньев системы на ее устойчивость
- •2.2.3. Изучение стандартных полиномов и диаграммы Вышнеградского
- •2.3. Содержание отчета
- •2.4. Контрольные вопросы
- •Методы коррекции систем автоматического управления
- •3.1. Основные сведения
- •3.2. Программа работы
- •3.3. Содержание отчета
- •Контрольные вопросы
- •Расчет и анализ систем подчиненного регулирования
- •4.1. Основные сведения
- •4.2. Программа работы
- •4.3. Содержание отчета
- •Контрольные вопросы
- •Синтез и исследование системы с модальным управлением
- •Основные сведения
- •5.2. Программа работы
- •5.3. Содержание отчета
- •Контрольные вопросы
- •Приложение Правила работы с системой Matlab 6.X/Simulink
- •1. Начало работы.
- •2. Работа в среде визуального моделирования Simulink.
- •Тираж 150 экз. Заказ 0.
- •197376, С.-Петербург, ул. Проф. Попова, 5
Контрольные вопросы
Как в зависимости от ПФ объекта следует выбирать тип регулятора и по каким формулам определяют его параметры при настройке на ОМ и СО?
Получить формулы для расчета параметров ПИД-регулятора при настройке контура на ОМ, если ПФ
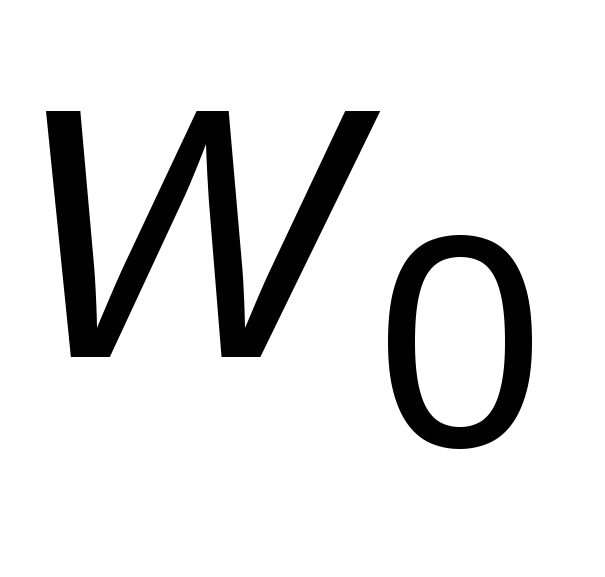 описывает апериодическое звено второго
порядка с постоянными времени
описывает апериодическое звено второго
порядка с постоянными времени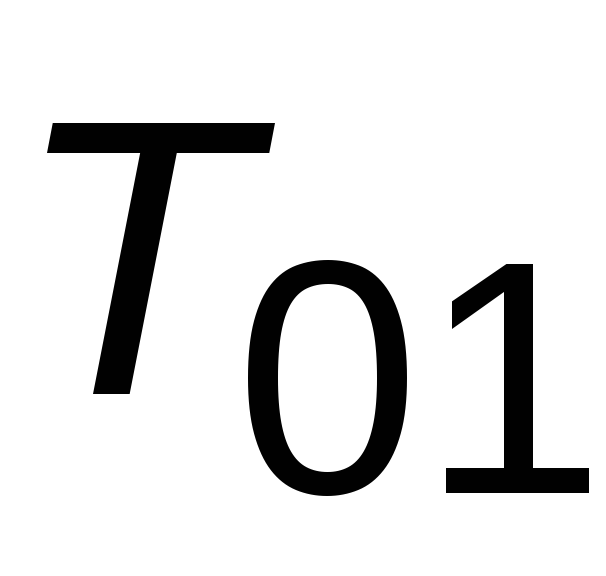 и
и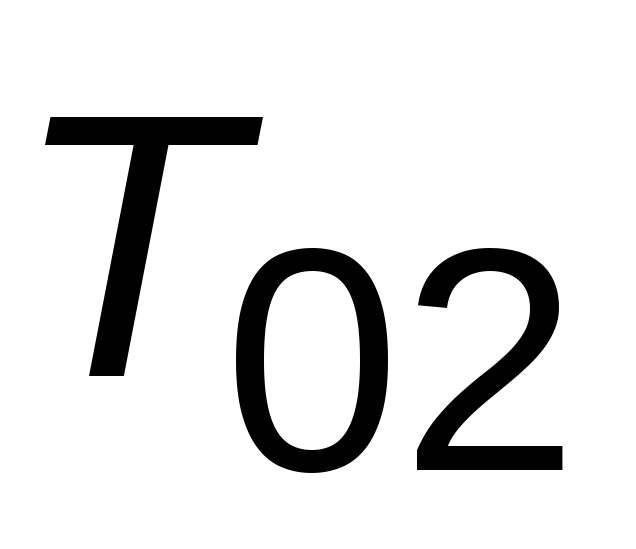 .
.Пояснить, каковы принципы настройки контуров на ОМ и СО (с помощью асимптотических ЛАХ).
Какими значениями показателей качества ПХ и частотных показателей качества характеризуются ОМ и СО?
Почему несколько звеньев с малыми постоянными времени при расчете СПР можно заменять одним звеном с суммарной постоянной времени?
Лабораторная работа № 5
Синтез и исследование системы с модальным управлением
Цель работы – освоение методики синтеза модального регулятора и анализ возможностей модального управления.
Основные сведения
Модальнымназывается управление,
обеспечивающее размещение корней
характеристического полинома (ХП) в
заданных точках комплексной плоскости.
В простейшем случае для исходной системы
(объекта управления) с одним входом,
описываемой уравнением![]() ,
гдеx– n-мер-ный вектор состояния,
аu– скалярное управление, модальный
регулятор (МР), представляющий собой
линейную обратную связь по состоянию,
описывается уравнением
,
гдеx– n-мер-ный вектор состояния,
аu– скалярное управление, модальный
регулятор (МР), представляющий собой
линейную обратную связь по состоянию,
описывается уравнением![]() ,
где
,
где![]() – задающее воздействие;
– задающее воздействие;![]()
![]() – матрица обратной связи;
– матрица обратной связи;![]() – коэффициент, назначением которого
можно обеспечить заданный коэффициент
передачи системы от входаg к заданному
выходуy. Если, например, требуется
синтезировать систему, удовлетворяющую
заданным требованиям к перерегулированию
– коэффициент, назначением которого
можно обеспечить заданный коэффициент
передачи системы от входаg к заданному
выходуy. Если, например, требуется
синтезировать систему, удовлетворяющую
заданным требованиям к перерегулированию![]() и времени регулирования
и времени регулирования![]() ,
то методика синтеза МР должна включать
в себя следующие этапы.
,
то методика синтеза МР должна включать
в себя следующие этапы.
Составить математическое описание объекта управления и записать матрицы АиВ.
Исследовать управляемость пары (А, В). Если матрица (


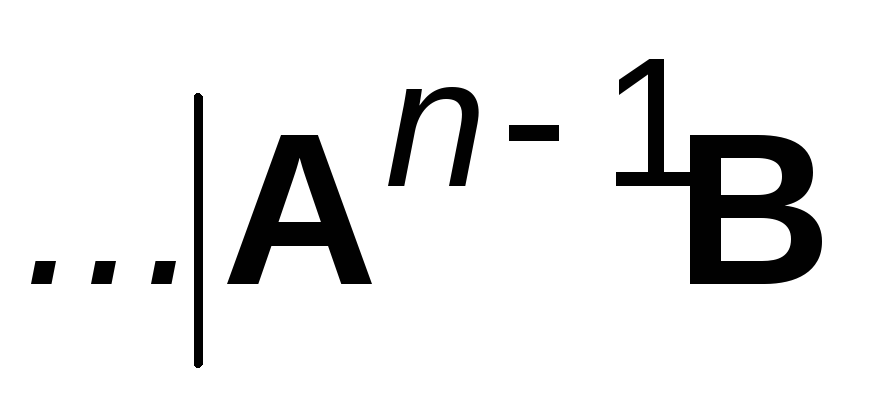 )
имеет полный ранг, то для данного объекта
может быть синтезирован МР.
)
имеет полный ранг, то для данного объекта
может быть синтезирован МР.Записать выражения для матрицы новой системы
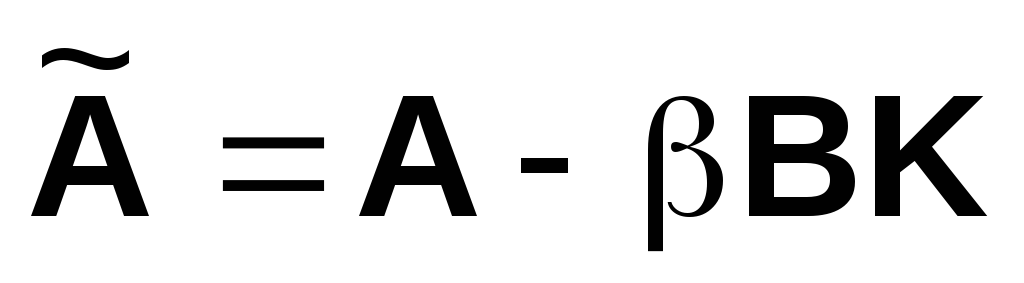 и ее ХП
и ее ХП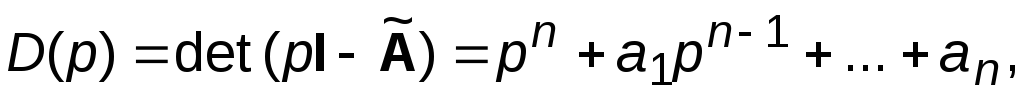 коэффициенты которого представляют
собой композиции параметров объекта
и неизвестных коэффициентов
коэффициенты которого представляют
собой композиции параметров объекта
и неизвестных коэффициентов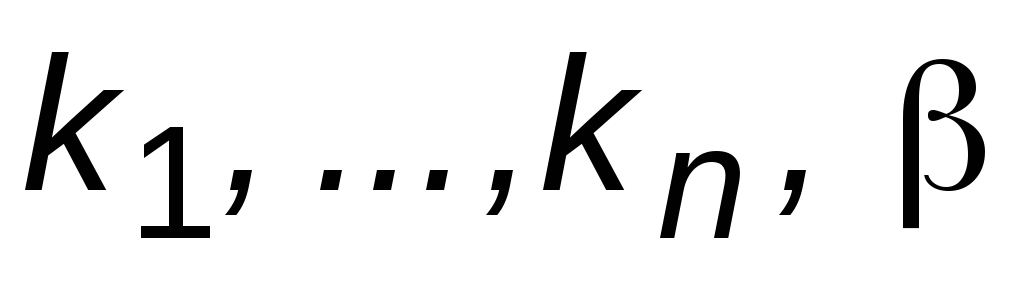 .
.В соответствии с заданным значением
 по справочнику выбрать тип стандартного
желаемого ХП
по справочнику выбрать тип стандартного
желаемого ХП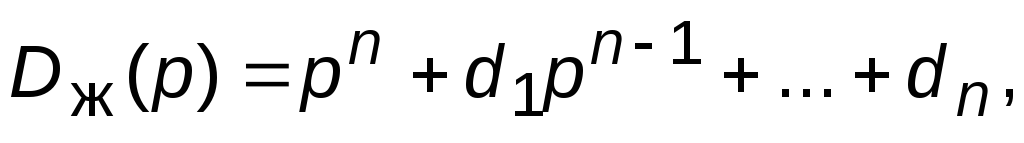 где
где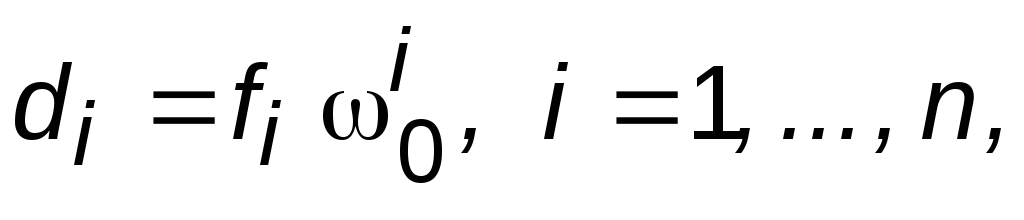 и выписать значения коэффициентов
и выписать значения коэффициентов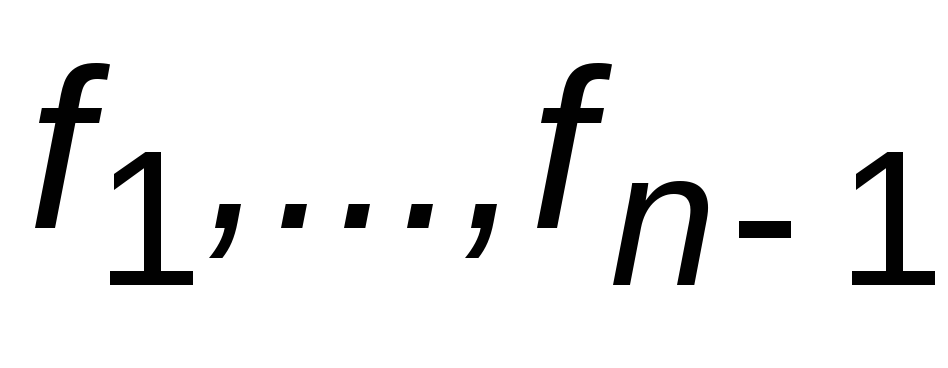 (
(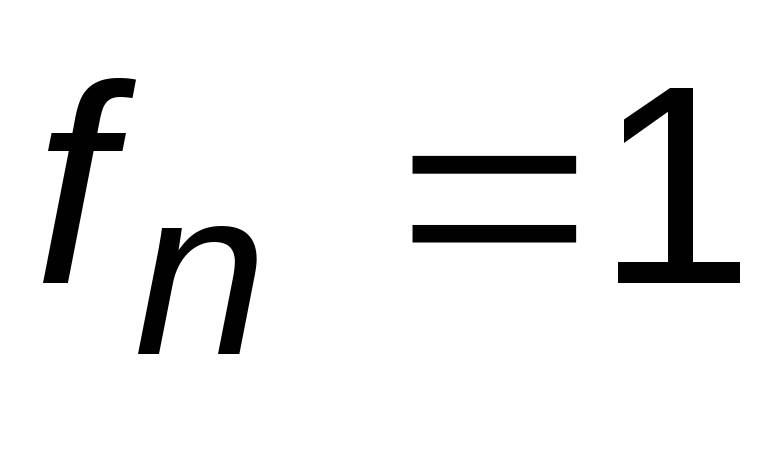 )
и относительного времени регулирования
)
и относительного времени регулирования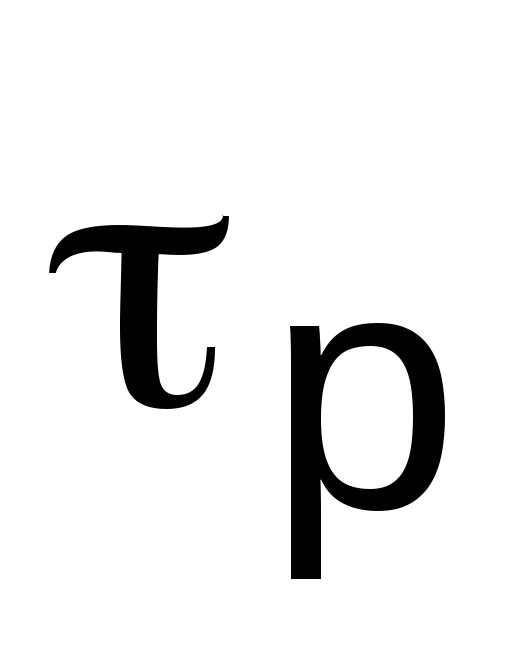 .
.Зная требуемое значение
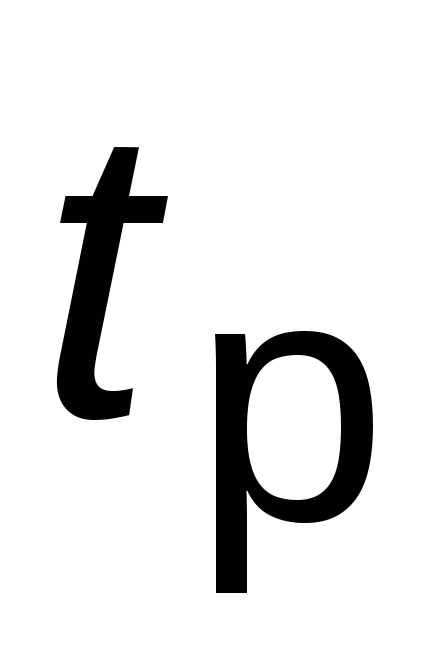 ,
вычислить среднегеометрический корень
полинома как
,
вычислить среднегеометрический корень
полинома как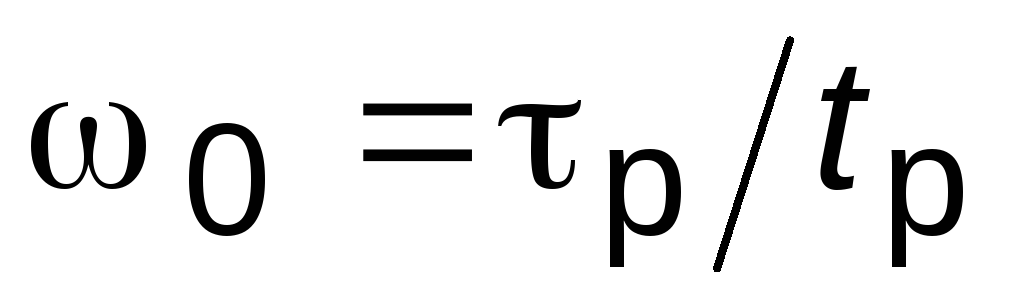 ,
после чего вычислить коэффициенты
,
после чего вычислить коэффициенты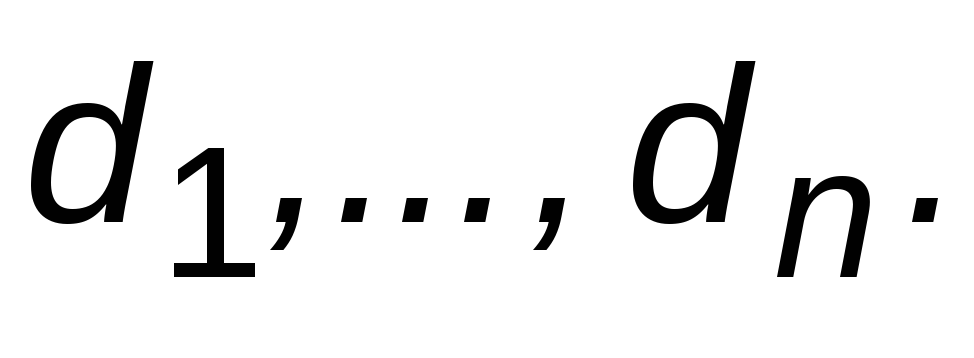
Выразить коэффициент передачи системы (требуемое значение которого известно) через коэффициенты
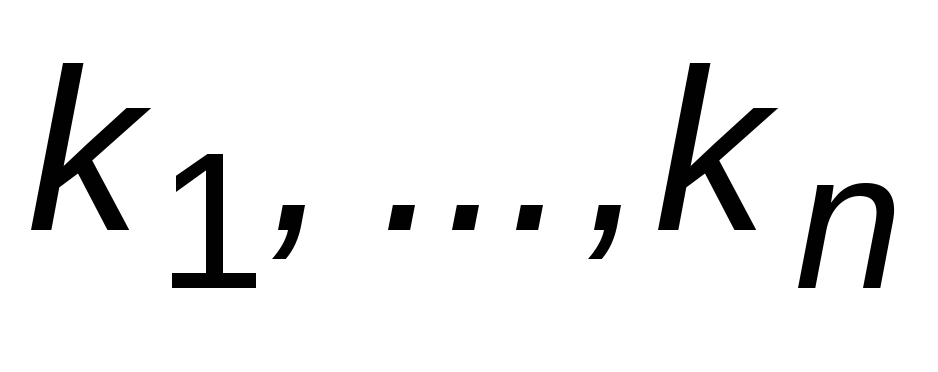 и, возможно,
и, возможно, .
.Приравнивая коэффициенты при одинаковых степенях p желаемого и фактического полиномов (
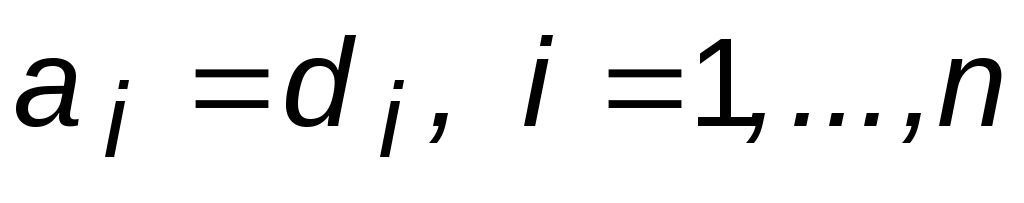 ),
составить системуn линейных
алгебраических уравнений. Дополнив ее
уравнением из предыдущего пункта и
решив, найти элементы
),
составить системуn линейных
алгебраических уравнений. Дополнив ее
уравнением из предыдущего пункта и
решив, найти элементы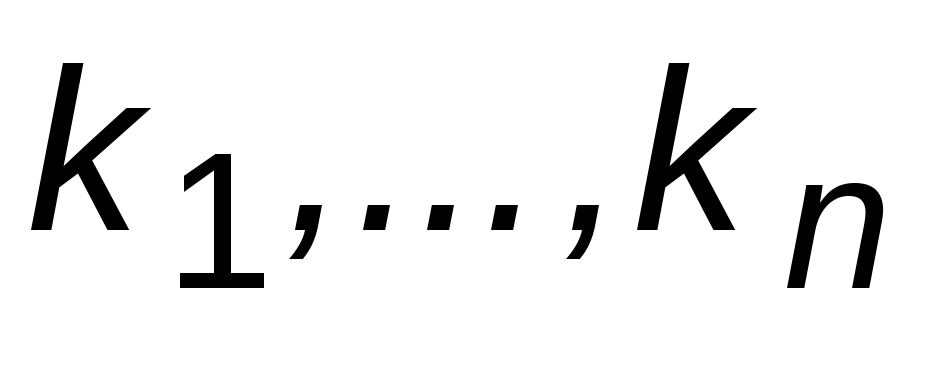 матрицы
матрицы и
коэффициент
и
коэффициент .
.
5.2. Программа работы
Объектом синтеза и анализа является
система регулирования скорости двигателя,
соединенного с механизмом упругой
кинематической связью. Исходная система
и система с МР представлены одной схемой
на рисунке, из которой исходная система
получается при
![]() = 10. На схеме
= 10. На схеме![]() и
и![]() – угловые скорости двигателя и механизма;
– угловые скорости двигателя и механизма;![]() –
задание скорости;
–
задание скорости;![]() – момент сопротивлений;
– момент сопротивлений;![]() – момент сил упругости;
– момент сил упругости;![]() с и
с и![]() с – постоянные времени двигателя
и механизма;
с – постоянные времени двигателя
и механизма;![]() с
и
с
и![]() – постоянная времени жесткости и
коэффициент внутреннего трения;– коэффициент, описывающий предварительный
усилитель и быстродействующий внутренний
контур регулирования тока.
– постоянная времени жесткости и
коэффициент внутреннего трения;– коэффициент, описывающий предварительный
усилитель и быстродействующий внутренний
контур регулирования тока.
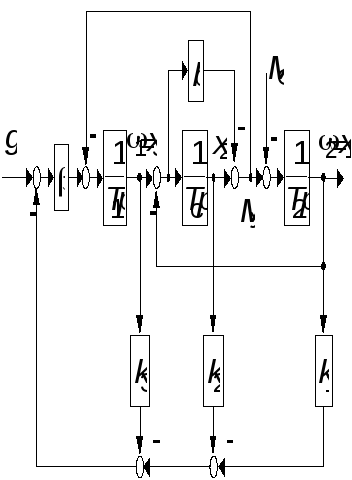
Работа состоит из двух этапов – подготовительного, выполняемого в домашних условиях, и исследовательского, выполняемого в лаборатории.
Задание для домашней подготовки:
определить параметры МР
![]() , использовав
методику из 5.1, для двух типов стандартных
полиномов – Баттерворта и биномиального
(их описания даны в лабораторной работе
№ 2). Значение
, использовав
методику из 5.1, для двух типов стандартных
полиномов – Баттерворта и биномиального
(их описания даны в лабораторной работе
№ 2). Значение![]() взять из вариантов, приведенных ниже:
взять из вариантов, приведенных ниже:
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
5 |
8 |
10 |
12 |
15 |
20 |
25 |
30 |
40 |
50 |
При расчете регулятора учесть, что в
исходной системе коэффициент передачи
равен единице, а в системе с МР равен
![]() ,
в силу чего получаем уравнение связи
,
в силу чего получаем уравнение связи![]() .
Для самопроверки: окончательные выражения
для параметров МР имеют следующий вид:
.
Для самопроверки: окончательные выражения
для параметров МР имеют следующий вид:
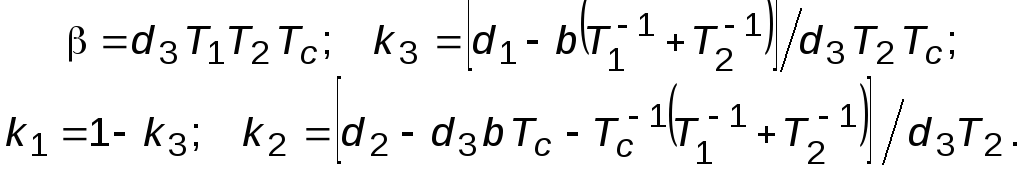
Исследовательская часть состоит из следующих этапов.
Выполнить анализ свойств исходной системы: получить ПХ по задающему воздействию (с копией экрана), считая выходной переменную
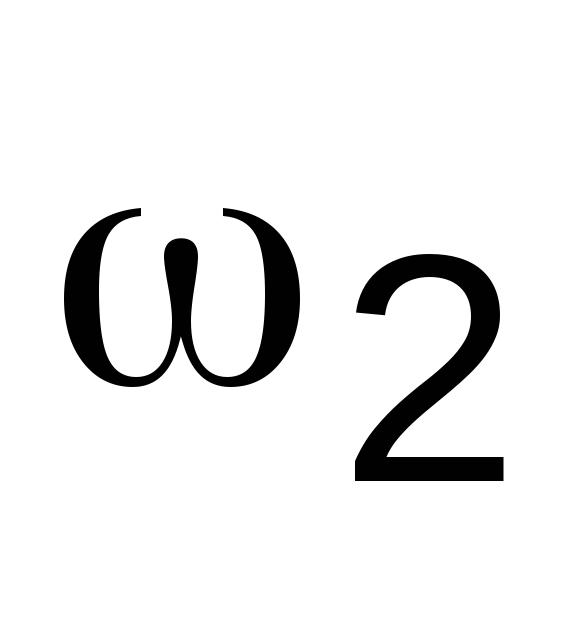 ,
и определить
,
и определить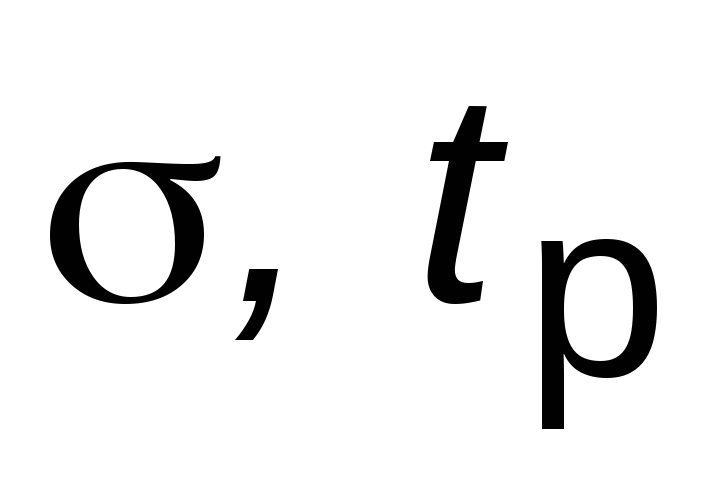 и частоту колебаний; определить
показатель колебательностиМ,
полосу пропускания
и частоту колебаний; определить
показатель колебательностиМ,
полосу пропускания и максимум
и максимум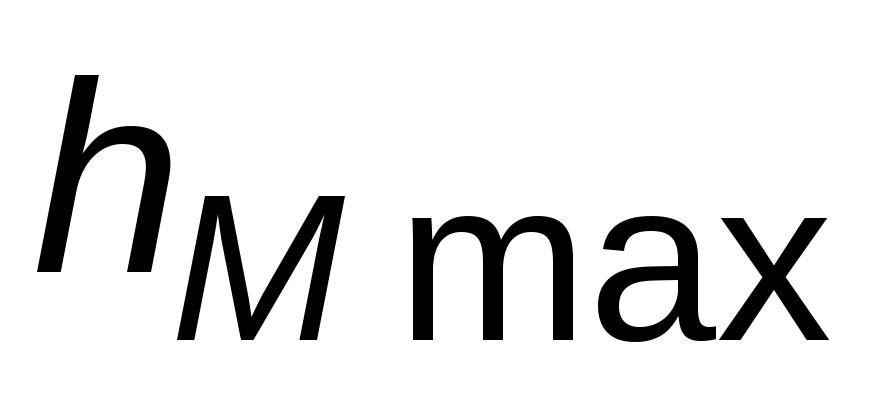 ПХ
по возмущению.
ПХ
по возмущению.Для каждого из двух вариантов назначения ХП выполнить анализ динамических свойств системы с МР, получив ПХ по задающему и возмущающему воздействиям и определив
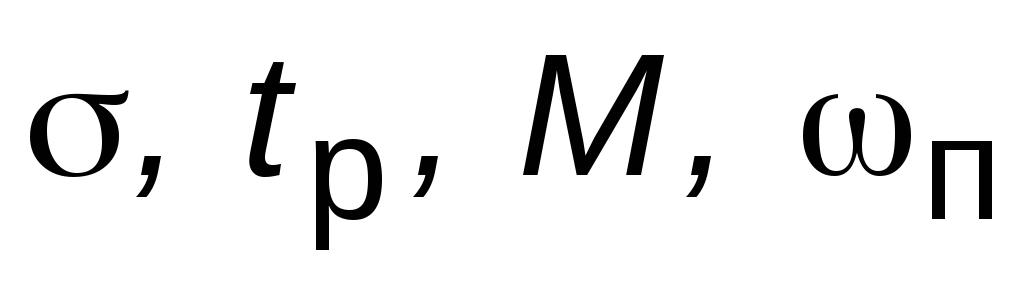 .
Для одной из ПХ сделать копию экрана.
.
Для одной из ПХ сделать копию экрана.
