
- •Список обозначений
- •Введение
- •I. Общие вопросы информационного обмена
- •I.1. Информационные поля и коммуникация
- •I.1.1. Фазы обращения информации
- •I.1.2. Виды информации
- •1.1.3.Структура информации
- •I.2. Количество информации
- •I.2.1.Структурные меры информации
- •1.2.2.Традиционные и нетрадиционные системы счисления
- •1.2.4. Информационные показатели измерений и контроля
- •I.2.5. Семантическая мера информации
- •1.3. Задания для самоконтроля и подготовки
- •2. Представление и отображение информации
- •2.1. Проблема передачи информации оператору
- •2.2. Виды информационных каналов
- •2.2.1. Механические каналы
- •2.2.2. Акустические каналы.
- •2.2.3. Оптические каналы
- •2.2.4. Электрические каналы
- •2.2.5. Радиотехнические каналы
- •2.3. Восприятие визуальной информации оператором
- •2.4. Восприятие аудиоинформации оператором
- •2.4.1. Модели слухового восприятия
- •2.4.2. Механическая модель слухового аппарата человека
- •2.4.3.Восприятие гармонических сигналов («чистых» тонов)
- •2.5. Задания для самоконтроля и подготовки
- •3. Звук. Основы информационного обмена в звуковых полях
- •3.1. Линейные характеристики звукового поля
- •3.1.1. Связь звукового давления с колебательной скоростью
- •3.1.2. Плоская волна
- •3.1.3. Модели волн с неплоским фронтом
- •3.2. Отражение и преломление плоских волн
- •3.2.1. Волновые процессы на плоской границе раздела сред
- •3.2.2. Взаимодействие упругих волн с плоским слоем
- •3.2.3. Волновые процессы на границе раздела движущихся сред
- •3.2.4. Явление полного внутреннего отражения
- •3.2.5. Отражение звука неровной поверхностью
- •3.2.6. Отражение звука искривленной поверхностью. Интеграл Кирхгофа
- •3.3. Эффект Доплера
- •Поскольку , то из (3.61) можно записать:
- •3.4. Задания для самоконтроля и подготовки
- •4. Заключение
- •5. Глоссарий
- •Ответы на тестовые задания и методически рекомендации по их выполнению
- •6. Предметный указатель
- •7. Литература
- •Содержание
2.5. Задания для самоконтроля и подготовки
Задание 2.1. Три
независимых источника работают с
интенсивностями
![]() ,
,![]() и
и![]() ,
соответственно. На сколько
,
соответственно. На сколько![]() «вырастет» интенсивность звука при их
совместной работе по сравнению с самым
«громким» источником?
«вырастет» интенсивность звука при их
совместной работе по сравнению с самым
«громким» источником?
1) на 3
![]() ;
2) на 6
;
2) на 6![]() ;
3) на 2
;
3) на 2![]() ;
4) на 83
;
4) на 83![]() ;
5) данных недостаточно.
;
5) данных недостаточно.
Задание 2.1. Нота «ля» первой октавы имеет частоту 440 Гц. На сколько отличается частота соседней с ней ноты «си»?
1) на 20 Гц; 2) на 26, 4 Гц; 3) на 440 Гц; 4) 1 Гц; 5) данных недостаточно.
Задание 2.3. На сколько будет отличаться фазовый сдвиг звуковых волн, воспринимаемых правым и левым ухом человека при «фронтальном» и «боковом» прослушивании сигнала, с частотой, при которой длина волны равна базовому расстоянию между слуховыми сенсорами взрослого человека?
1) 2π; 2) π; 3) 0; 4) π/2; 5) π/4.
3. Звук. Основы информационного обмена в звуковых полях
В данном разделе…
Основные физические величины звукового процесса
Взаимодействие упругих волн с плоскими границами раздела сред
Отражение звука на шероховатой границе раздела сред
Рассеяние упругих волн объектами произвольной формы
Информационный обмен между подвижными источниками и приемниками звука
3.1. Линейные характеристики звукового поля
3.1.1. Связь звукового давления с колебательной скоростью
Звуковое поле - одна из форм существования материи, проявляемая в виде кинетической и потенциальной энергии, колеблющихся материальных тел - звуковых волн в твердой, жидкой и газообразной средах, обладающих свойствами упругости формы и объекта [6-8]. Частоты звуковых (слышимых) колебаний находятся в полосе частот от 20 до 20000Гц. Инфразвуковые, ультразвуковые и гиперзвуковые колебания органом слуха человека не воспринимаются.
Колеблющееся тело, являющееся источником звука, приводит в движение примыкающие к нему частицы упругой среды, которые, в свою очередь, заставляют колебаться соседние с ним частицы. Процесс распространения колебаний в упругой среде называют волной. Направление распространения звуковых волн называют звуковым лучом, а поверхность, соединяющую все точки с одинаковой фазой колебания частиц - фронтом волны. Фронт волны в каждый момент времени перпендикулярен звуковому лучу.
В отличие от твердых тел, где возможно распространение волн как с продольным, та и с поперечным направлением смещения частиц по отношению к направлению распространения волн, в жидкостях и газах волна распространяется только в направлении колебательного движения самих частиц среды. Такой процесс характерен для продольных волн или волн сжатия, представляющих собой последовательность чередующихся сгущений и разрежений частиц среды.
Расстояние между
двумя соседними
сгущениями (разрежениями) называется
длиной волны .
В чередующихся, например, в воздухе,
слоях сжатия или разряжения среды
происходит изменение давления по
сравнению с атмосферным (статическим)
давлением. Разность между мгновенным
давлением звукового поля в данной точке
![]() и статическим (атмосферным)
и статическим (атмосферным)![]() называют звуковым давлением:
называют звуковым давлением:![]() .
Звуковое давление
.
Звуковое давление![]() -
величина знакопеременная. В моменты
сжатия среды оно положительно:
-
величина знакопеременная. В моменты
сжатия среды оно положительно:![]() >
>![]() ,
а в момент разряжения - отрицательно,
т.е.
,
а в момент разряжения - отрицательно,
т.е.![]() <
<![]() (рис. 3.1).
(рис. 3.1).
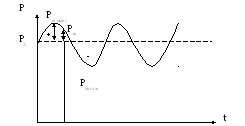
Рис. 3.1
Звуковое давление
в системе СИ измеряется в Паскалях.
Давление в 1 Паскаль (Па) создается при
действии силы в 1 ньютон (Н) на поверхность
площадью 1м2.
Ясно, что 1 Па в 105
раз меньше 1 атмосферы. В акустике
типичные значения давлений при
информационном обмене лежат в пределах
100 Па. Скорость распространения звука
в воздухе сильно зависит от метеорологических
условий и температуры. В последнем
случае с достаточной для практики
точностью можно записать:
![]() ,
гдеТ
– абсолютная температура, а размерность
скорости звука – м/с.
,
гдеТ
– абсолютная температура, а размерность
скорости звука – м/с.
Колебательное
движение частиц среды при распространении
звуковой волны характеризуется также
колебательным смещением (от положения
покоя), которое происходит с определенной
скоростью, именуемой колебательной:
![]() .
Производная по времени от колебательной
скорости образует колебательное
ускорение.
.
Производная по времени от колебательной
скорости образует колебательное
ускорение.
Не следует путать
эту скорость со скоростью распространения
звука -
![]() .
Скорость звука есть величина постоянная
для этой среды, и зависит от внешних
факторов. Колебательная скорость,
обычно, на несколько порядков меньше
.
Скорость звука есть величина постоянная
для этой среды, и зависит от внешних
факторов. Колебательная скорость,
обычно, на несколько порядков меньше![]() ,
и возрастает с увеличением частоты и
амплитуды акустического сигнала.
,
и возрастает с увеличением частоты и
амплитуды акустического сигнала.

Колебательную
скорость считают положительной, если
частицы среды смещаются в направлении
движении волны, и отрицательной, если
эти движения встречные. Если источник
звука совершает колебания по гармоническому
закону с линейной частотой
![]() ,
то за времяT,
в течение которого происходит один
период колебательного процесса, фронт
звуковой волны перемещается на расстоянии,
численно равное длине волны -
,
то за времяT,
в течение которого происходит один
период колебательного процесса, фронт
звуковой волны перемещается на расстоянии,
численно равное длине волны -
![]() .
Очевидно, что одну секунду волна
распространится на расстояния численно
равные
.
Очевидно, что одну секунду волна
распространится на расстояния численно
равные![]() .
.
Выделим в звуковом
поле элементарный объем воздуха,
заключенный между боковыми поверхностями
![]() ,
находящимися на расстоянии
,
находящимися на расстоянии![]() друг от друга перпендикулярными к
направлению звуковых лучей.
друг от друга перпендикулярными к
направлению звуковых лучей.
Очевидно, что масса
воздуха в выделенном объеме равна
![]() ,
где
,
где![]() - плотность среды. Среда в рассматриваемом
объеме находится под действием разности
давлений
- плотность среды. Среда в рассматриваемом
объеме находится под действием разности
давлений![]() и
и![]() .
Следовательно, сила, под действием
которой может происходить движение
этого объема воздуха:
.
Следовательно, сила, под действием
которой может происходить движение
этого объема воздуха:![]() .
.
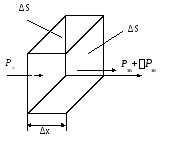
х
Рис.3.2
Если под действием
приложенной силы
![]() элементарный объем воздуха с массой
элементарный объем воздуха с массой![]() приобретает ускорение
приобретает ускорение![]() ,
то по второму закону Ньютона сила
инерции:
,
то по второму закону Ньютона сила
инерции:![]() ,
откуда переходя к производным, устремив
,
откуда переходя к производным, устремив![]() ,
получим:
,
получим:
![]() .
(3.1)
.
(3.1)
Данное уравнение
(3.1) и называют уравнением движения среды
при прохождении звука. При такой записи
учитывается только одномерное движение
по координате
![]() .
При трехмерном движении, получим:
.
При трехмерном движении, получим:
![]() ,
(3.2)
,
(3.2)
где
![]() -
единичные векторы – орты осей декартовой
системы координат. Дополнительной
величиной, характеризующей звуковое
поле, является потенциал. Различают
потенциал скорости и потенциал смещения.
Скалярный потенциал скорости определяется
как:
-
единичные векторы – орты осей декартовой
системы координат. Дополнительной
величиной, характеризующей звуковое
поле, является потенциал. Различают
потенциал скорости и потенциал смещения.
Скалярный потенциал скорости определяется
как:
![]() .
(3.3)
.
(3.3)
Скалярный потенциал скорости связан со звуковым давлением соотношением:
![]() .
(3.4)
.
(3.4)
В теоретической акустике показано, что при учете адиабатического характера звукового процесса для газовой среды уравнение (3.1) может быть преобразовано (с учетом 3.3 и 3.4) в волновое уравнение:
![]() ,
(3.5)
,
(3.5)
где
![]() -
скорость распространения звука в газовой
среде;
-
скорость распространения звука в газовой
среде;![]() -
оператор-лапласиан. Волновое уравнение
может быть записано также для давления
и колебательной скорости звука. Для
гармонических процессов, протекающих
с частотой
-
оператор-лапласиан. Волновое уравнение
может быть записано также для давления
и колебательной скорости звука. Для
гармонических процессов, протекающих
с частотой![]() ,
волновое уравнение (3.5) можно преобразовать
в уравнение Гельмгольца:
,
волновое уравнение (3.5) можно преобразовать
в уравнение Гельмгольца:
![]() ,
(3.6)
,
(3.6)
где
![]() -
волновое число. Общее решение уравнения
Гельмгольца (3.6) в декартовых координатах
(для волнового процесса, распространяющегося
вдоль оси «х»),
имеет вид:
-
волновое число. Общее решение уравнения
Гельмгольца (3.6) в декартовых координатах
(для волнового процесса, распространяющегося
вдоль оси «х»),
имеет вид:
![]() .
(3.7)
.
(3.7)
В уравнении (3.7)
каждое слагаемое соответствует волне,
распространяющейся в «положительном»
или «отрицательном» направлении оси
«х». Выбор знака зависит от выбора знак
во «временном» множителе
![]() .
.
