
ТВ-1-2-3 + ИДЗ-ТВ-1
.doc
ГЛАВА Теория вероятностей.
§1. Случайный эксперимент (СЭ). Математическая модель СЭ.
Эксперимент ≡ исследование ≡ наблюдение ≡ опыт ≡ …
СЭ :1) возможность многократного повторения ; 2) «априорная неоднозначность» результата - - исхода ω конкретного эксперимента из множества W возможных исходов - W = { ω }.
В дальнейшем
- все взаимоисключающие исходы ω СЭ будем называть «элементарными событиями»;
- будем считать, что множество элементарных событий W дискретное - конечное W ={w1,,…, wn } или счетное W ={wi; i=1,2,…. }
Определение 1.1.
(Дискретным) Пространством элементарных событий(ПЭС) называется любое полное множество W ={w} возможных элементарных событий случайного эксперимента.
Построение математической модели СЭ начинается с построения ПЭС.
СЭ1 – «бросание игральной кости»: wi - номер выпавшей грани →ПЭС: W1 = {1,2,3,4,5.6}; W2 ={чет., нечет.}; W3 ={1,не 1} НО : {1,чет}, {1,чет, нечет} – НЕ ПЭС !!
CЭ2
–
«стрельба по мишени до первого поражения».
![]() -
количество израсходованных патронов
→
-
количество израсходованных патронов
→
W = {1,2,3,.... }- счетное бесконечное ПЭС.
Пусть
в СЭ W
={ wi
; i=1,2,...,n} выполнена серия
из m
испытаний,
причем в mi
случаях
![]() зафиксирован исход wi
и
относительная частота исхода
wi
- mi
= mi
/m
:
зафиксирован исход wi
и
относительная частота исхода
wi
- mi
= mi
/m
:
![]()
!!! В ТВ рассматриваются лишь такие СЭ, которые обладают свойством устойчивости относительных частот исходов : при многократном повторении длинных серий случайного эксперимента относительные частоты mi исходов wi, как правило, меняются мало и при неограниченном увеличении длины серии "сходятся, концентрируются, сгущаются" к числу Pi Î[0,1] -
![]()
Определение
2.1.
Если
каждому элементарному событию
![]() поставлено в соответствие число pi=P(wi)
:
piÎ[0,1]
и
поставлено в соответствие число pi=P(wi)
:
piÎ[0,1]
и
![]() ,
,
это
число называется
вероятностью элементарного
события/исхода
wi,
а
а
множество
![]() называется распределением
вероятностей на ПЭС
называется распределением
вероятностей на ПЭС
![]() .
Пару
множеств
.
Пару
множеств
![]() называют
математической
моделью дискретного случайного
эксперимента.
называют
математической
моделью дискретного случайного
эксперимента.

СЭ1:
СЭ2:
§2. Cлучайные события и их вероятности. Алгебра событий.
Теория вероятностей «начинается» с задания (построения) математической модели СЭ и решает задачу нахождения вероятности случайного события в рамках заданной математической модели.
Пусть
задана (выбрана, построена) математическая
модель дискретного СЭ: {W
; PW}.![]()
Определение
1.2. Случайным
Событием
A
на
дискретном
ПЭС W
называется
любое
его
подмножество А={wА}ÌW,
при
этом составляющие случайное
событие
элементарные исходы
wАÎА
называются
благоприятными
для случайного события А:
если
эксперимент закончился одним из
благоприятных исходов wА,
говорят,
что в результате СЭ произошло
случайное
событие
А.
В
частности, событиями на ПЭС W
являются:
-
![]() ;
;
![]() .
.
![]() На
конечном
ПЭС
На
конечном
ПЭС
![]() определено
2n
случайных
событий.
определено
2n
случайных
событий.
Определение
2.2.
(Аксиома аддитивности).
Вероятностью
P(A)
События А![]() называется
число P(A),
равное сумме вероятностей элементарных
событий, благоприятных А:
называется
число P(A),
равное сумме вероятностей элементарных
событий, благоприятных А:
А![]()
Замечание. Поскольку определения 1.2 и 2.2 даны «на языке множеств», дадим вероятностную интерпретацию «алгебры событий» - операций над множествами благоприятных исходов.
Пусть
![]()
1.
Произведением событий А и В
называется
событие С,
содержащее все исходы, благоприятные
для событий А
и
В
одновременно:
![]() , при
этом
, при
этом
События А и В называются несовместными, если они не имеют общих исходов, т.е.
![]() [1]
[1]
События
А и В
называются
независимыми,
если
![]()
2 .
Суммой событий А и В
называется
событие С,
содержащее все исходы
.
Суммой событий А и В
называется
событие С,
содержащее все исходы
![]() ,
благоприятные
для события А
или
события В:
,
благоприятные
для события А
или
события В:
![]()
Теорема
сложения. Вероятность
суммы событий равна сумме вероятностей
этих событий минус вероятность их
произведения:
![]() [2]
[2]
Событие
![]() называется
противоположным
событию
А,
называется
противоположным
событию
А,
если оно состоит из всех исходов, неблагоприятных для А, т.е
.
![]()
 [3]
[3]
ЭКЗ +1. Доказать формулу:
![]() [4]
[4]
Пример.
![]()
«А
- выпала грань с нечетным номером»
![]()
B - "номер грани кратен 3"; Û В={3,6};P(B)=2/6. А+В={1,3,5,6} Þ P(A+B)=4/6=2/3;
A∙B={3}
ÞР(А∙В)=1/6
P(A+B)=P(A)+P(B)-P(AB)=
![]()
Алгоритм решения задачи нахождения вероятности события С в случайном эксперименте :
(I)
построить
(задать, выбрать) математическую модель
СЭ
-
 ,
определить
на
W
случайное
событие
С={wС}ÌW
и
вычислить
«по
определению»
P(С)
=
,
определить
на
W
случайное
событие
С={wС}ÌW
и
вычислить
«по
определению»
P(С)
=
![]()
ИЛИ
(2) определить С и вычислить Р(С), используя алгебру событий и формулы [1-4]:
![]() [1]
[1]
![]() [2]
[2]
 [3]
[3]
![]() [4]
[4]
§3 Классическое распределение вероятностей. Основные формулы комбинаторики.
Рассмотрим дискретный СЭ, все «элементарные исходы» которого равновозможны. Соответствующую мат. модель С. Э. называют "классической".
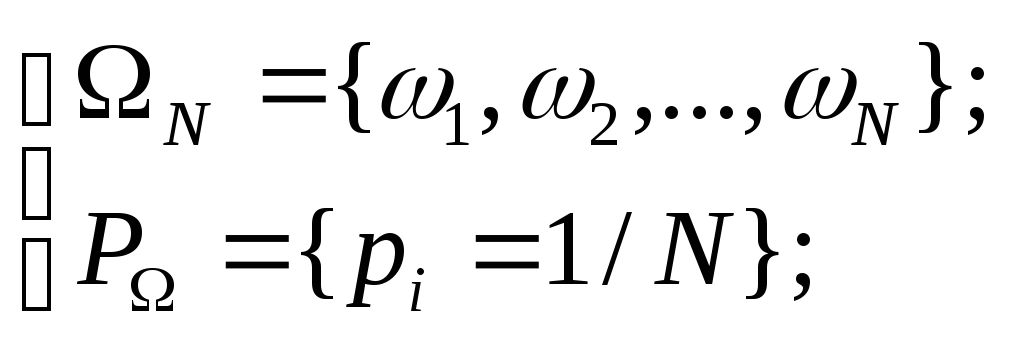
Очевидно,
что в рамках классической модели
вероятность события
![]() равна
отношению числа благоприятных исходов
равна
отношению числа благоприятных исходов
![]() к
размерности П.Э.С. NΏ:
к
размерности П.Э.С. NΏ:
![]()
Пример.
В
урне находятся 29 пронумерованных шаров.
Найти вероятность того, что номер
вынутого НАУГАД шара кратен 3
![]() ---------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------
.
Пусть
![]() -
множество "n"
различных
элементов, из которых составляются
различные
m
–местные комбинации/наборы
K(n,m),
содержащие “m”
элементов:
-
множество "n"
различных
элементов, из которых составляются
различные
m
–местные комбинации/наборы
K(n,m),
содержащие “m”
элементов:

- упорядоченные наборы - последовательности различаются либо порядком, либо составом элементов
n=4,m=3→(b1,b2,b3 ) ¹(b2,b1,b3 )¹ (b4,b1,b3 ),
- неупорядоченные наборы различаются только составом элементов ,включенных в комбинацию:
{b1,b2,b3 } ={b2,b1,b3} ≠ {b4,b1 ,b3}
![]()
.
Основное
правило комбинаторики
:"Если
для «построения комбинации» необходимо
последовательно выполнить «операции»
:
![]() ,
причем
,
причем
![]() Ai
можно выполнить ni
способами
и после этого Ai+1
можно выполнить ni+1
способами, количество таких различных
комбинаций равно
Ai
можно выполнить ni
способами
и после этого Ai+1
можно выполнить ni+1
способами, количество таких различных
комбинаций равно
![]() .
.
Рассмотрим некоторые m-местные комбинации из n различных элементов.
1.
Размещениями из n
по
m
без
повторений
называются
m-местные
последовательности
![]() .
Так как элемент a1
можно выбрать
n1=n
способами,
после
этого
a2-
n2=n-1,
…, am-
nm=n-m+1
способами,
по ОПК количество таких различных
комбинаций равно
.
Так как элемент a1
можно выбрать
n1=n
способами,
после
этого
a2-
n2=n-1,
…, am-
nm=n-m+1
способами,
по ОПК количество таких различных
комбинаций равно
![]() (1)
(1)
2.
Перестановками n
элементов без повторений
называются
n-местные
последовательности
![]() ,различающиеся
порядком элементов, т.е. размещения из
n
по n.
Поэтому
,различающиеся
порядком элементов, т.е. размещения из
n
по n.
Поэтому
NПЕР
=P(n)=![]() =n!
(2)
=n!
(2)
3.
Сочетаниями из n
по
m
без
повторений
называются неупорядоченные
m-местные
комбинации
![]() .Очевидно,
что если в каждом сочетании
выполнить
перестановки его m-элементов,
получим размещения из n
по m.
Следовательно
.Очевидно,
что если в каждом сочетании
выполнить
перестановки его m-элементов,
получим размещения из n
по m.
Следовательно
![]() (3)
(3)
Свойства
сочетаний:
![]()
Утверждение.
n-
элементное
множество
![]() имеет
имеет
![]() подмножеств,
включая пустое множество и Bn,
при этом количество
k-
элементных подмножеств равно
подмножеств,
включая пустое множество и Bn,
при этом количество
k-
элементных подмножеств равно
![]() .
.
Пусть
![]() и
имеется неограниченное количество
«копий» каждого элемента.
и
имеется неограниченное количество
«копий» каждого элемента.
4.
Размещениями из n
по
m
с
повторениями
называются m-местные
последовательности
![]() ,
элементы которых
,
элементы которых
![]() могут
повторяться. Так как каждый элемент
последовательности ai,
i=1,2,…,m
можно выбрать ni=n
способами,
по ОПК количество таких различных
комбинаций равно
могут
повторяться. Так как каждый элемент
последовательности ai,
i=1,2,…,m
можно выбрать ni=n
способами,
по ОПК количество таких различных
комбинаций равно
N = nm (4)
Пример
1. Записать
все различные комбинации 1.- 4. для
![]()
![]()
Пример 2. Сколькими способами можно разместить 5 различных «шаров» по 8 «бездонным» ящикам?
![]()
Сколькими способами можно разместить 5 различных «шаров» по 8 «одноместным» ящикам?
![]()
ИДЗ-ТВ1 ПО ТЕМЕ «Непосредственный подсчет вероятностей. Алгебра событий».
Задание.
0) «Известно ,что:» - используемые определения и формулы.
Задача 1). Выбрать по условиям задачи ПЭС, построить математическую модель СЭ, определить случайное событие и вычислить его вероятность.
Задача 2). Найти вероятность случайного события, используя «алгебру событий».
Результаты – с 3 в.з.ц.
1.[1] Найти вероятность того, что в лотерее «5 из 49» угаданы хотя бы 4 номера.
(1)
Примем
за элементарные исходы ω
случайного эксперимента сочетания
из 49 номеров по
5.
![]()
Математическая
модель случайного эксперимента:

(2)
Случайное событие A={ωA}![]() ,
ωA
– такие
сочетания
из 49 по 5,
в которых угаданы
4(А4)
или 5(А5)
фиксированных чисел, т.е. А
= А4+А5.
Так
как события А4
и А5
несовместные, P(A)=P(A4)+P(A5).
,
ωA
– такие
сочетания
из 49 по 5,
в которых угаданы
4(А4)
или 5(А5)
фиксированных чисел, т.е. А
= А4+А5.
Так
как события А4
и А5
несовместные, P(A)=P(A4)+P(A5).
(3) По основному правилу комбинаторики:
--------------------------------------------------------
2.[1] «9 друзей наугад заказали билеты на поезд из 5 вагонов. Найти вероятность того, что друзья оказались в одном или в двух соседних вагонах».
-
Примем за исходы случайного эксперимента девятиместные комбинации номеров вагонов, доставшихся 1-му, 2-му, …, 9-му другу, - размещения из 5 по 9 с повторениями NΩ= 59
-
Определим случайное событие А как сумму СС: А=А1+А2с (все попали в какой-либо один или в какие-то два соседние вагона). Так как СС А1 и А2с несовместные, Р(А)= Р(А1)+Р(А2с).
-
А1: (выбрать один «общий» вагон) NА1 =5 А2с: (выбрать два соседних вагона из 5) (разместить 9 по 2-м выбранным вагонам,
n2c=4 {{1,2}, {2,3}, {3,4}, {4,5}}
исключая 2 варианта: все в одном или все в другом из двух вагонов !!) n(9,2) = 29-2 NА2с = n(9,2)∙ n2c=4∙(29-2) NА=N(A1)+ N(A2с)
-
Р(А)=
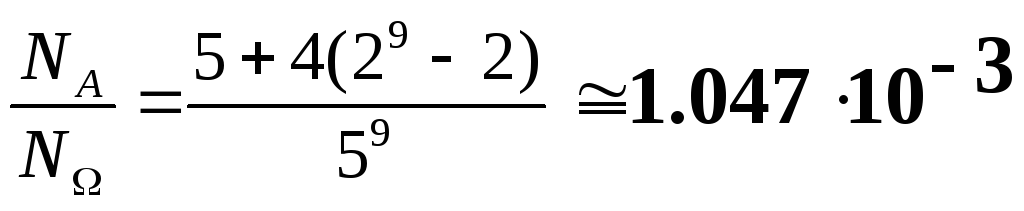
Результат.
А=А1+А2с.
Р(А)=
Р(А1)+Р(А2с);
Р(А)=
![]()
3.[1] « В ящике находятся 20 деталей, 5 из которых – стандартные. Найти вероятность того, что из трех взятых наугад деталей по крайней мере одна окажется стандартной».
(1)
Примем за пространство элементарных
исходов Ω={ω}, ω - сочетания из 20 различных
деталей по 3. Размерность NΩ=![]() .
.
(2) Случайное событие А={ ωA}, ωA – такие сочетания из 20 по 3, в которых из 3 деталей либо одна, либо две, либо три – стандартные
Противоположное
СС
![]() такие
сочетания
из
20 по 3,
в
которых все 3 детали
нестандартные.
такие
сочетания
из
20 по 3,
в
которых все 3 детали
нестандартные.
![]()
Результаты:


4.[2] Найти вероятность того, что студент сдаст хотя бы два экзамена из трёх, если результаты экзаменов независимы и вероятности сдачи 1,2,3-го экзаменов равны: p1=p3=0.9, р2=0.8.
![]()

Результаты:
![]()
=======================================================================
Литература.
1)Даугавет А.И., Постников Е.В., Червинская Н.М. Введение в теорию вероятностей.: Учеб. пособие, СПбГЭТУ «ЛЭТИ» - 2012.
2) Бородин А.Н. Элементарный курс теории вероятностей и математической статистики: Учеб. пособие для вузов. СПб, Лань,2008.
3) Вентцель Е.С., Овчаров А.А. Теория вероятностей и ее инженерные приложения. Учеб. пособие для вузов.- М.: Наука, 2000, 2003
4) Вентцель Е.С., Овчаров А.А. Задачи и упражнения по теории вероятностей: Учеб. пособие для вузов.- М.: Высшая школа, 2002, 2004, 2005. Самостоятельная работа. Зачет.
ИДЗ-1 “Непосредственный подсчет вероятностей. Алгебра событий» ИДЗ-2 «Формула полной вероятности. Формула Байеса. Схема Бернулли» ИДЗ-3 «Дискретная и непрерывная случайная величина».
ИДЗ-4 «Функции случайной величины».

