4. Теорема единственности. Аналитическое продолжение

Аналитические функции, в некоторых отношениях, очень похожи на многочлены.

Теорема.Нули аналитической функции, отличной от тождественного нуля, изолированы, т. е. у каждой точки, где аналитическая функция обращается в ноль, существует окрестность, не содержащая других нулей этой функции.

Доказательство.Пусть функция аналитична в окрестности точкии, тогда найдется достаточно малый круг, в котором функция допускает разложение в ряд Тейлора. Из предположенияследует, что, но поскольку функция не равна нулю тождественно, то существуют ненулевые коэффициенты. Пусть– первый из них, тогда ряд Тейлора этой функции можно представить в виде

Можно подобрать число такое, что в кругевыполнено неравенствои, следовательно, в этом круге функция имеет единственный корень.

Основная теорема алгебры утверждает, что многочлен -й степени имееткорней. Аналитическая функция, как многочлен «бесконечной» степени может иметь бесконечное число корней, например,Но на расположение корней имеется жесткое ограничение: они не могут сгущаться.

Теорема единственности.Если функция является аналитической в областии, то.

Доказательство.В силу непрерывности, и точкаоказывается корнем функции, в любой окрестности которого имеются другие корни. Такое возможно только для.

Рассмотрим теперь свойства аналитических функций, которые не возможны для многочленов.

Определение. Если функция является аналитической в круге круги, то существует числотакое, что разлагается в ряд Тейлора в круге. Если эту процедуру можно продолжать и за конечное число шагов перейти в точку, то говорят, что функция допускает аналитическое продолжение из точкив точку.

Разумеется, такая процедура для многочленов возможна всегда, но для аналитических функций общего вида это не так. Функцию не возможно продолжить из точкив точку. Более того, вполне благополучную в кольцефункциюможно продолжать из точкии вернуться в ту же точку, но при этом окажется, что значение функции будет другим. Процедура аналитического продолжения выводит на многолистные аналитические функции. Это полезные и важные объекты, познакомится с ними можно по книге [3].

Рассмотренные свойства составляют исчерпывающую картину поведения аналитической функции во внутренних точках области аналитичности. Теперь следует обратиться к рассмотрению точек, где аналитичность нарушается.

5. Особые точки. Ряды Лорана

Функция аналитическая в точке обязательно аналитична в некоторой окрестности этой точки, но это не означает, что функцию можно продолжить в любую точку, двигаясь от окрестности к окрестности. Дело в том, что размер окрестности может очень маленьким. Рассмотрим пример того, как может «исчезать» аналитичность: функция сходится при любом, но если положить, то ряд разойдется, поскольку. Поведение аналитической функции при приближении к границе области аналитичности может быть очень сложным, эти вопросы выходят далеко за рамки вводного курса.

Другая причина потери аналитичности связана с невозможностью определить функцию, как однозначную в окрестности точки. Нельзя отказаться от рассмотрения этой ситуации, потому что она возникает при решении такой банальной задачи, как квадратное уравнение. Рассмотрим функцию . Напомним, что можно определить корень двумя способами (две ветви корня)

Вычислим значения в двух близких точках

Если , то оба аргумента стремятся к 1, но значения функций стремятся соответственно к 1 и -1. Такого рода точки называют точками ветвления.

Здесь будет рассмотрен только простейший вариант нарушения аналитичности.

Определение.Точканазывается изолированной особой точкой функции, если существует числотакое, что в «проколотом круге»функция аналитична и однозначна, т.е. любое аналитическое продолжение функции вдоль замкнутой кривой сохраняет значение функции в стартовой точке.

Не приходится ожидать, что в окрестности изолированной особой точки функцию удастся разложить в ряд Тейлора, но представить функцию виде ряда более сложного вида всегда возможно.

Определение.Рядом Лорана называется следующее выражение:

Говорят, что ряд Лорана сходится в кольце , рядсходится при, а рядсходится при.

Примеры.1) Исследуем сходимость ряда Лорана. Перепишем ряды в более привычной форме. Первый ряд сходится при, второй при, т. о. ряд Лорана сходится в кольце.

2) «Похожий» ряд расходится, т. к. рядсходится при, а ряд сходится только при.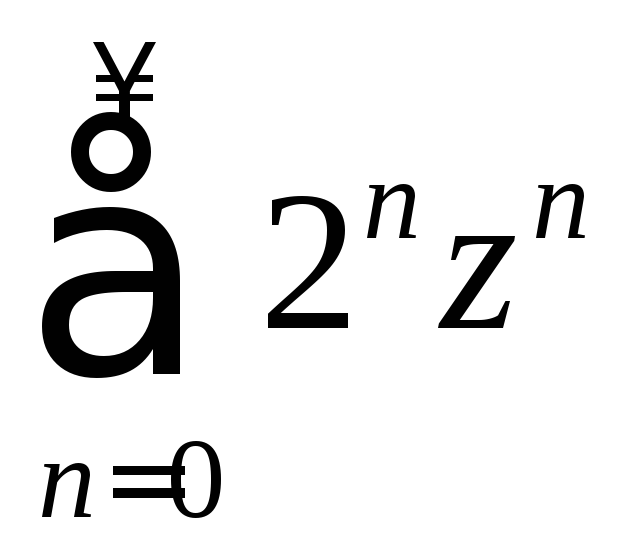

Введенной конструкции достаточно, что бы разложить в ряд любую аналитическую функцию в окрестности изолированной особой точки.

Теорема. (о разложении в ряд Лорана)Если– изолированная особая точка функции , то в проколотой окрестности точкиона допускает разложение в ряд Лорана

План доказательства.Фиксируем точку. Рассмотрим пару окружностей, лежащих внутри кольца и таких, что точкалежит между ними:

.

Соединим окружности отрезком, не проходящим через точку , и сформируем из них положительно ориентированный контур, обходящий точкув положительном направлении и не содержащий внутри себя особых точек функции . Представим с помощью формулы Коши и применим рассуждение, использованное в доказательстве теоремы о разложении в ряд Тейлора. На внешней окружности оно пройдет без изменений (важно, что) и получится часть ряда Лорана с положительными коэффициентами. На внутренней окружности справедливо противоположное неравенство, что изменит ход тождественных преобразований и даст, в результате часть ряда Лорана с отрицательными коэффициентами.

Поведение функции в окрестности изолированной особой точки может быть различным. Эти различия хорошо улавливаются следующим определением.

Определение.Классификация изолированных особых точек.

Пусть -- изолированная особая точка функции.

называют устранимой особой точкой, если функция ограничена в проколотом круге,

называют полюсом, если,

называют существенной особой точкой во всех остальных случаях.

Примеры.

1) для функции , точкаявляется устранимой особой точкой,

2) для функции , точкииявляются полюсами,

3) для функции , точкаявляется существенно особой точкой, действительно,и, следовательно, функция не ограничена,, следовательно, функция не имеет предела в точке.

Проследим, как выглядят ряды Лорана в каждом из этих случаев

1)

2) чтобы получить ряд Лорана в изолированной особой точкедостаточно разложить в ряд второе слагаемое

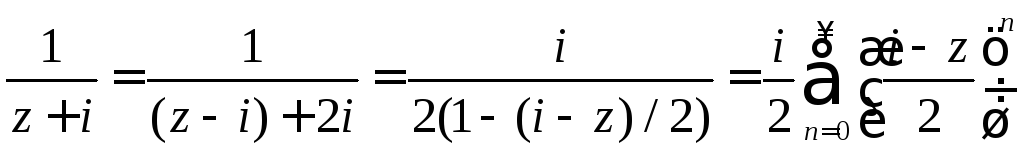
Следовательно

3)

Внешне банальная, классификация особых точек приобретает глубокий смысл благодаря замечательной связи с рядами Лорана.

Теорема (об эквивалентной классификации).Пусть– изолированная особая точка функции,– ее ряд Лорана. Тогда:

1) – устранимая особая точка(ряд Лорана не содержит слагаемых с отрицательными степенями);

2) – полюссуществует числотакое, что(ряд Лорана содержит конечное число слагаемых с отрицательными степенями);

3) – существенно особая точкадля всякого положительного числасуществуеттакое, что(ряд Лорана содержит бесконечное число слагаемых с отрицательными степенями).

Для доказательства теоремы потребуется простая, но полезная оценка:

Неравенство Коши

Если функция аналитична в кругеипри, то

Доказательство неравенства. В теореме о разложении в ряд Лорана доказано, что . В качестве контура интегрирования можно взять окружность, далее простые оценки по модулю завершают доказательство.

Доказательство теоремы об эквивалентной классификации.

1) Из условия равенства нулю коэффициентов с отрицательными номерами следует аналитичность функции в круге , и, следовательно, она ограничена в этом круге, т. е.-- устранимая особая точка.

Покажем, что верно и обратное. Пусть в.

Воспользуемся неравенством Коши при любом. Для отрицательныхполучим, посколькуможет быть сколь угодно малым, то.

2) Предположим, что существует положительное число такое, чтои. Тогда свойства степенных функций, гарантируют, что в достаточно малой окрестности точкисправедлива оценка. Следовательно-- точка полюса.

Проверим обратное утверждение. Если известно, что -- точка полюса, то, причеманалитическая функция и. Можно доказать, что в этих условиях функциятакже является аналитической. Это следует из следующего простого свойства степенных рядов: если степенной рядсходится прии, тои ряд сходится при.

С учетом этого утверждения и очевидно.

3) Достаточно, заметить, что если модуль функции не ограничен и не стремится к бесконечности, то он не может иметь предела. Аналогично доказывается обратное утверждение.