
- •Часть 1
- •Введение
- •1. Особенности машинной арифметики, точность вычислений на эвм (Лабораторная работа №1)
- •2. Изучение понятия Обусловленности вычислительной задачи (Лабораторная работа №2)
- •3. Решение нелинейных уравнений
- •3.1. Общие сведения
- •3.2. Метод бисекции (Лабораторная работа №3)
- •3.3. Метод хорд (Лабораторная работа №4)
- •3.4. Метод Ньютона (Лабораторная работа № 5)
- •3.5. Метод простых итераций (Лабораторная работа №6)
- •3.6. Курсовая работа по дисциплине и варианты заданий
- •4. Численное интегрирование
- •4.1. Составные формулы прямоугольников, трапеций, Симпсона. (Лабораторная работа №6)
- •4.2. Формула Гаусса. (Лабораторная работа №7)
- •Библиографический список
- •1. Особенности машинной арифметики, точность вычислений на эвм 5
4. Численное интегрирование
4.1. Составные формулы прямоугольников, трапеций, Симпсона. (Лабораторная работа №6)
Повышения точности численного интегрирования добиваются путем применения составных формул. Для этого при нахождении определенного интеграла отрезок
 разбивают на четное
разбивают на четное число отрезков длины
число отрезков длины и на каждом из отрезков длины
и на каждом из отрезков длины применяют соответствующую формулу.
Таким образом получают составные
формулы прямоугольников, трапеций и
Симпсона.
применяют соответствующую формулу.
Таким образом получают составные
формулы прямоугольников, трапеций и
Симпсона.На сетке
 ,
, ,
, ,
составные формулы имеют следующий вид:
,
составные формулы имеют следующий вид:формула прямоугольников
 ;
;формула трапеций
 ;
;формула Симпсона
 ,
,где
 -остаточные
члены. При
-остаточные
члены. При
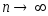 приближенные значения интегралов для
всех трех формул (в предположении
отсутствия
погрешностей
округления) стремятся к точному значению
интеграла [1,7,8].
приближенные значения интегралов для
всех трех формул (в предположении
отсутствия
погрешностей
округления) стремятся к точному значению
интеграла [1,7,8].Для практической оценки погрешности квадратурной можно использовать правило Рунге. Для этого проводят вычисления на сетках с шагом
 и
и ,
получают приближенные значения интеграла
,
получают приближенные значения интеграла и
и и за окончательные значения интеграла
принимают величины:
и за окончательные значения интеграла
принимают величины: -
для формулы прямоугольников;
-
для формулы прямоугольников;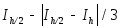 -
для формулы трапеций;
-
для формулы трапеций; -
для формулы Симпсона.
-
для формулы Симпсона.За погрешность приближенного значения интеграла для формул прямоугольников и трапеций тогда принимают величину
 ,
а для формулы Симпсона
,
а для формулы Симпсона .
.В лабораторной работе №6 требуется, используя квадратурные формулы прямоугольников, трапеций и Симпсона, вычислить значения заданного интеграла и, применив правило Рунге, найти наименьшее значение
 (наибольшее значение шага
(наибольшее значение шага ),
при котором каждая из указанных формул
дает приближенное значение интеграла
с погрешностью
),
при котором каждая из указанных формул
дает приближенное значение интеграла
с погрешностью ,
не превышающей заданную.
,
не превышающей заданную.Порядок выполнения лабораторной работы №6.
Составить программы-функции для вычисления интегралов по формулам прямоугольников, трапеций и Симпсона.
Составить программу-функцию для вычисления подынтегральной функции.
Составить головную программу, содержащую оценку по Рунге погрешности каждой из перечисленных выше квадратурных формул, удваивающих
 до тех пор, пока погрешность не станет
меньше
до тех пор, пока погрешность не станет
меньше ,
и осуществляющих печать результатов:
значения интеграла и значения
,
и осуществляющих печать результатов:
значения интеграла и значения для каждой формулы.
для каждой формулы.Провести вычисления по программе, добиваясь, чтобы результат удовлетворял требуемой точности.
Результаты работы оформить в виде краткого отчета, содержащего сравнительную оценку применяемых для вычисления формул.
Варианты заданий приведены в таблице 4.1 (
 =
0.01; 0.001; 0.0001).
=
0.01; 0.001; 0.0001).
4.2. Формула Гаусса. (Лабораторная работа №7)
В квадратурной формуле Гаусса

узлы
 и коэффициенты
и коэффициенты подобраны так, чтобы формула была точна
для всех многочленов степени
подобраны так, чтобы формула была точна
для всех многочленов степени .
Для приближенного вычисления интеграла
по конечному отрезку
.
Для приближенного вычисления интеграла
по конечному отрезку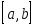 выполняется замена переменной
выполняется замена переменной ;
тогда квадратурная формула Гаусса
принимает вид[2,8,12]
;
тогда квадратурная формула Гаусса
принимает вид[2,8,12]
Таблица 4.1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
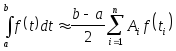 ,
,
где
 ;
; - узлы квадратурной формулы Гаусса;
- узлы квадратурной формулы Гаусса; - гауссовы коэффициенты
- гауссовы коэффициенты .
.Если подынтегральная функция достаточно гладкая, то формула Гаусса обеспечивает очень высокую точность при небольшом числе узлов.
В лабораторной работе №7 требуется, используя квадратурную формулу Гаусса наивысшего порядка точности, вычислить приближенное значение заданного интеграла.
Интеграл предлагается вычислить по квадратурной формуле Гаусса с восемью узлами:
 ,
,
 ;
; ,
, ;
; ,
, ;
; ,
, .
.Порядок выполнения лабораторной работы №7.
Составить программу-функцию для вычисления интеграла по формуле Гаусса.
Составить программу-функцию для вычисления значений подынтегральной функции.
Составить головную программу, содержащую обращение к вычислительным процедурам и осуществляющую печать результатов.
Результаты работы оформить в виде краткого отчета, содержащего характеристику используемого метода вычислений, его точности и полученное значение интеграла.
Варианты заданий к лабораторной работе приведены в таблице 4.2.
