3.2. Метод бисекции (Лабораторная работа №3)

147. Если найден отрезок [a,b], такой, что (a)(b), существует точка c, в которой значение функции равно нулю, т.е. (с)=0, с(a,b). Метод бисекции состоит в построении последовательности вложенных друг в друга отрезков, на концах которых функция имеет разные знаки. Каждый последующий отрезок получается делением пополам предыдущего. Процесс построения последовательности отрезков позволяет найти нуль функции (корень уравнения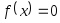с любой заданной точностью.

148. Рассмотрим один шаг итерационного процесса. Пусть на (n-1)-м шаге найден отрезок [a_n-1, b_n-1][a, b], такой, что (a_n-1)(b_n-1). Разделим его пополам точкой (a_n-1 +b_n-1)/2 и вычислим (). Если ()=0, то =( a_n-1+b_n-1)/2- корень уравнения. Если (), то из двух половин отрезка выбирается та, на концах которой функция имеет противоположные знаки, поскольку искомый корень лежит на этой половине, т.е.

149. a_n=a_n-1, b_n= , если (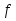)(a_n-1) < 0 ;

150. a_n=, b_n= b_n-1 , если 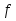(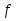)(a_n-1) > 0 .

151. Если требуется найти корень с точностью , то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше 2. Тогда координата середины отрезка есть значение корня с требуемой точностью .

152. Метод бисекции является простым и надежным методом поиска простого корня уравнения (простым называется корень x=c дифференцируемой функции , если (с) и (с)). Этот метод сходится для любых непрерывных функций , в том числе недифференцируемых. Скорость его сходимости невысока. Для достижения точности необходимо совершить Nlog₂(b-a)/ итераций. Это означает, что для получения каждых трех верных десятичных знаков необходимо совершить около 10 итераций.

153. В лабораторной работе №3 предлагается, используя программы - функции BISECT и Round из файла methods.cpp (файл заголовков metods.h, директория LIBR1), найти корень уравнения методом бисекции с заданной точностьюEps, исследовать зависимость числа итераций от точности Eps при изменении Eps от 0.1 до 0.000001, исследовать обусловленность метода (чувствительность к ошибкам в исходных данных).

154. Выполнение работы осуществляется по индивидуальным вариантам заданий (нелинейных уравнений), приведенным в подразделе 3.6. Номер варианта для каждого студента определяется преподавателем.

155. Порядок выполнения работы должен быть следующим:

1. Графически или аналитически отделить корень уравнения (т.е. найти отрезки[Left, Right], на которых функция 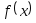удовлетворяет условиям теоремы Коши).

2. Составить подпрограмму вычисления функции .

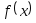3. Составить головную программу, содержащую обращение к подпрограмме f(x), BISECT, Round и индикацию результатов.

4. Провести вычисления по программе. Построить график зависимости числа итераций от Eps.

5. Исследовать чувствительность метода к ошибкам в исходных данных. Ошибки в исходных данных моделировать с использованием программы Round, округляющей значения функции с заданной точностью Delta.

156. Текст программы-функции BISECT, предназначенной для решения уравнения методом бисекции, представлен в подразделе 3.7.