Неорганическая химия / Физическая химия / Еремин В.В., Каргов С.И., Успенская И.А., Кузьменко Н.Е., Лунин В.В. Основы физической химии. В 2-х ч. / Основы физической химии

цис-стильбен транс-стильбен Закон действующих масс записывается следующим образом (индексы, отно-

сящиеся к обратным реакциям, часто записывают с отрицательным знаком):

r = r1 − r−1,

d[A] (21.1)

− dt = k1[A] − k−1[B].

Если начальные концентрации веществ A и B обозначить соответственно a и b и ввести степень превращения x ([A] = a − x, [B] = b + x), то кинетическое уравнение приобретает вид

dx

dt = k1(a − x) − k−1(b + x). (21.2)

Решение этого уравнения удобно записать через степень превращения x∞, соответствующую достижению равновесия:

где значение равновесной степени превращения x∞ определяется условием равенства скоростей прямой и обратной реакций:

Уравнения (21.3) для обратимой реакции первого порядка имеют такой же вид, как и уравнения (18.3), (18.4) для необратимой реакции, с той разницей, что вместо начальной концентрации фигурирует равновесная, а константу скорости необратимой реакции заменяет сумма констант для прямой и обратной реакций.

При t → ∞ наступает равновесие, которое характеризуется константой

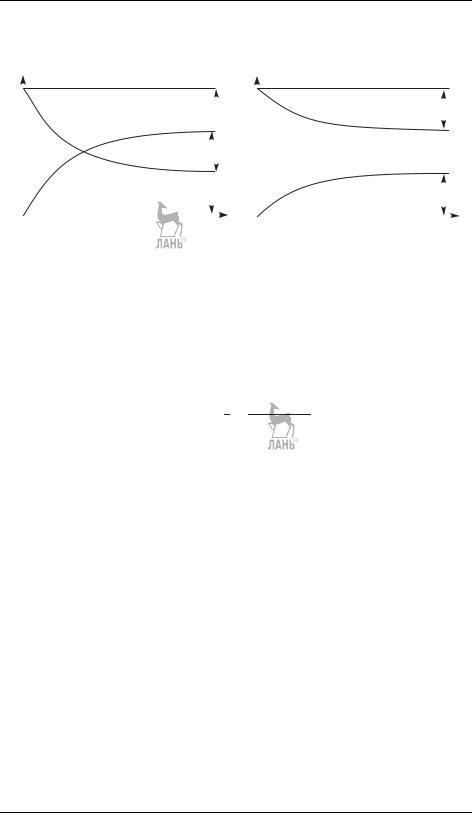
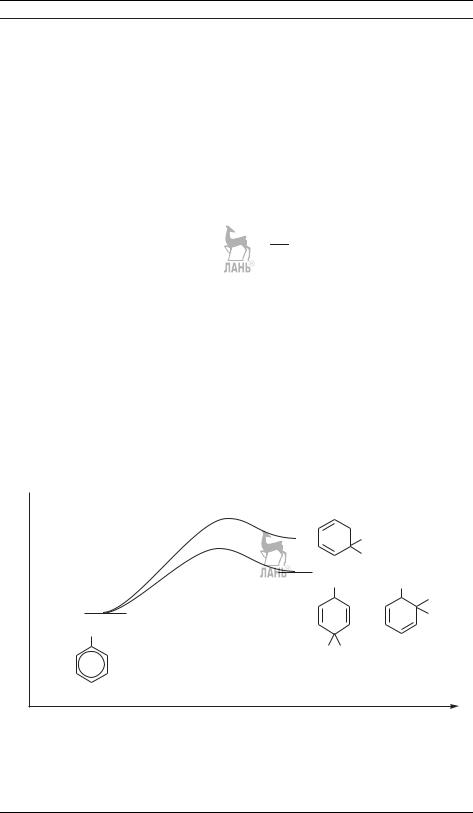
Если сначала в системе присутствовало только вещество A, то решение прямой задачи через концентрации реагирующих веществ имеет вид

[A] = [A]∞ + ([A]0 − [A]∞) exp [−(k1 + k−1)t] ,

(21.6)

[B] = [B]∞ (1 − exp [−(k1 + k−1)t]) .

Концентрация реагента монотонно убывает от начального значения до равновесного, а концентрация продукта монотонно растет от нуля до равновесия.

образуются три различных σ-комплекса, соответствующие орто-, мета- и па- ра-ориентации нитрогруппы.

Рассмотрим простейшую кинетическую схему

k1 B

A

k2

D

Кинетическое уравнение записывается с учетом принципа независимости:

r = r1 + r2,

Решение этого уравнения имеет такой же вид, как и для одной реакции первого порядка:

Запишем выражения для скоростей образования продуктов реакции:

Поделив одно уравнение на другое, находим, что в любой момент времени отношение концентраций продуктов постоянно и определяется константами скорости элементарных стадий:

Данная операция — частный случай довольного общего приема — исключения времени, который используют при построении фазовых портретов сложных реакций (см. § 28).

Конкретные выражения для концентраций продуктов получаются при интегрировании уравнений (21.12), например с начальным условием [B]0 = 0:

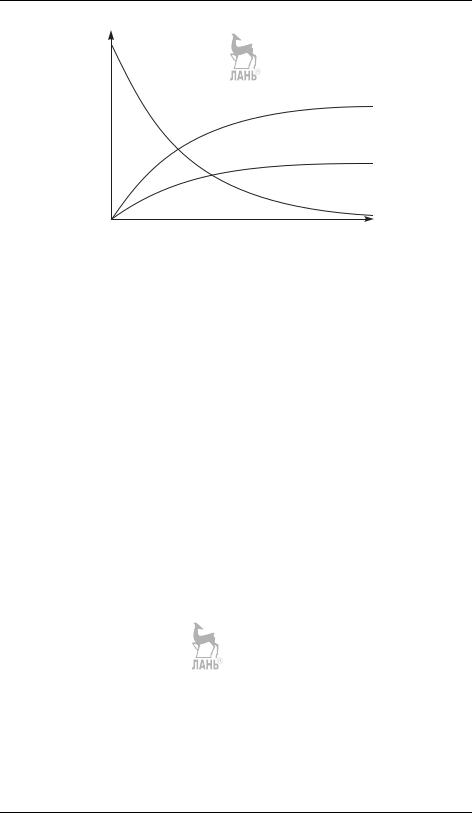
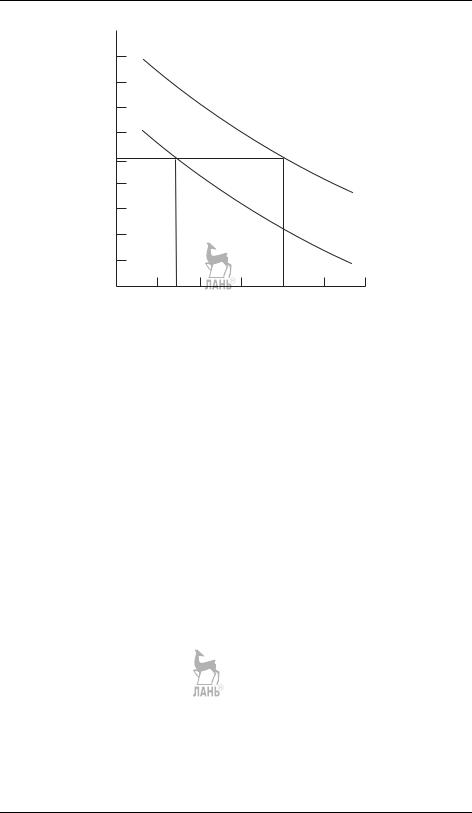
и аналогично для [D]. Кинетические кривые для параллельных реакций первого порядка приведены на рис. 21.3.

Обратная задача решается легко. По любой из трех кинетических кривых находят сумму констант скорости k1 + k2, а по отношению концентраций продуктов в любой момент времени — отношение констант k1/k2.

Если скорости параллельных реакций сильно различаются по порядку величины, то среди них можно выделить лимитирующую стадию, т. е. ту

элементарную реакцию, скорость которой определяет общую скорость процесса.

В параллельных реакциях лимитирующей является самая быстрая стадия. Это видно из выражения (21.13): если r1 r2, то r = r1 + r2 ≈ r1.

a

A → B

A → D

B

c

D

A

t

Рис. 21.3. Зависимости концентраций реагентов и продукта от времени для параллельных реакций первого порядка (k1 > k2)

Термодинамический и кинетический контроль

Интересная картина получается, если объединить два рассмотренных выше типа реакций и рассмотреть конкурирующие обратимые реакции:

A B

A D

Если соотношение конкурирующих продуктов определяется кинетическими параметрами, т. е. константами скорости прямых реакций, то речь идет о кинетическом контроле, если же оно задается термодинамическими параметрами — константами равновесия K1 = k1/k−1 и K2 = k2/k−2, то говорят о термодинамическом контроле процесса. Разумеется, термодинамический контроль может реализоваться только в том случае, когда в обеих реакциях за время опыта достигается равновесие. Если же обе реакции или хотя бы одна из них практически необратимы, возможен только кинетический контроль.

Вучебниках по органической химии обычно отмечают, что решающим фактором, определяющим тот или иной контроль реакции, является температура. Считается, что низкая температура способствует кинетическому контролю, тогда из двух продуктов больше получается того, у которого прямая реакция протекает быстрее. При высокой же температуре преимущественно образуется более устойчивый продукт, обладающий меньшей энергией Гиббса. Хорошим примером служит реакция гидробромирования бутадиена

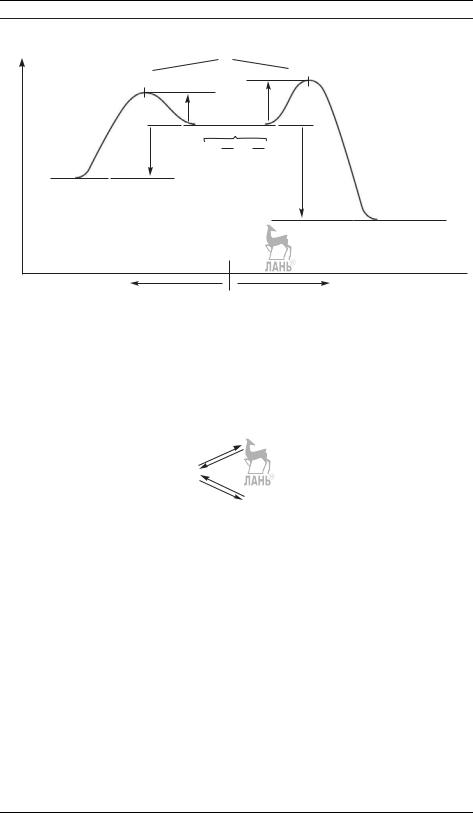
CH2=CH–CH=CH2 + HBr, которая протекает через образование промежуточного карбокатиона и приводит к продукту 1,2- или 1,4-присоединения (рис. 21.4). 1,2-Продукт обладает большей энергией Гиббса, но характеризуется меньшей энергией активации — он образуется при низкой температуре, в условиях кинетического контроля. 1,4-Продукт, напротив, медленнее образуется (большая´ энергия активации), но более устойчив, поэтому его образованию способствуют условия термодинамического контроля, т. е. более высокая температура.

Впринципе, этот подход правильный, он подтвержден многочисленными экспериментальными данными по зависимости выхода конкурирующих органических реакций от температуры. Но мы можем взглянуть на эту ситуацию и с

Рис. 21.4. Энергетические кривые конкурирующих реакций 1,2- и 1,4-присоединения HBr к CH2=CH–CH=CH2

другой точки зрения, кинетической, и доказать, что соотношение термодинамического и кинетического контроля — это вопрос не только температуры, но

ивремени. Будем считать, что в обеих реакциях возможно равновесие.

Вкачестве примера рассмотрим параллельные реакции дегидратации бутанола-2:

практического установления равновесия) реакций через τB и τD.

В начальный период времени, при t τB, τD, когда обратными реакциями можно пренебречь и концентрация продуктов еще мала, соотношение веществ B и D определяется, как и в необратимых реакциях, константами скорости k1 и k2:

Это кинетический контроль. Напротив, в конце процесса, когда в обеих реакциях установилось равновесие, т. е. при t τB, τD, концентрации веществ

t

T

Рис. 21.5. Влияние времени и температуры на термодинамический и кинетический контроль (τ1 и τ2 — времена релаксации, τ1 < τ2)

определяются только константами равновесия:

Таким образом, при любой температуре в начале конкурирующих реакций преобладает кинетический контроль, а в конце — термодинамический. Продолжительность действия того или иного контроля определяется временами релаксации. При низких температурах времена релаксации велики по сравнению со временем эксперимента (практически бесконечны), поэтому все время преобладает кинетический контроль. При высоких температурах равновесие устанавливается быстро, поэтому большую´ часть времени реакции действует термодинамический контроль. Характерное соотношение времени и температуры при выборе между кинетикой и термодинамикой показано на рис. 21.5.

Последовательные реакции

Необратимые последовательные реакции первого порядка — одна из самых широко распространенных моделей при изучении зависящих от времени систем. Рассмотрим простейшую схему, включающую всего две реакции:

k1 k2

A −→ B −→ D.

Решим прямую задачу. Пусть в начальный момент времени есть только вещество A. Применив к этой системе закон действующих масс и принцип незави-

симости химических реакций, получим систему дифференциальных уравнений

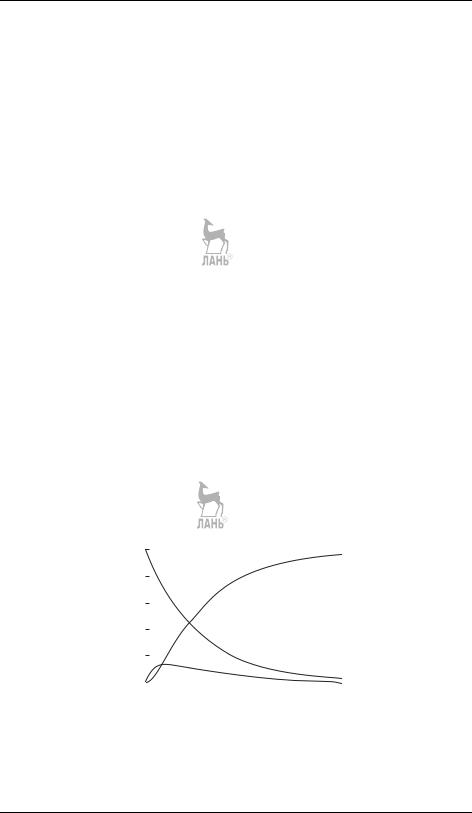
Не решая этой системы, можно сразу сделать некоторые качественные выводы о кинетических кривых. Вещество A распадается по необратимой реакции первого порядка, его концентрация экспоненциально убывает со временем. Концентрация интермедиата B равна нулю в начале и в конце реакции, следовательно, в какой-то промежуточный момент времени она достигает максимального значения (рис. 21.6). В этом момент времени d[B]/dt = 0, поэтому [B]max = (k1/k2)[A]. Значение максимальной концентрации B определяется отношением констант скорости — это может быть использовано при решении обратной задачи. Если k1 k2, то вещество B быстро накапливается и медленно расходуется, его максимальная концентрация почти достигнет исходной концентрации реагента a. Если же k2 k1, то промежуточный продукт не успевает образоваться в заметных количествах, он тут же превращается в продукт D

иего концентрация в любой момент времени мала (рис. 21.7). В этом случае для анализа кинетических уравнений можно использовать приближенный метод квазистационарных концентраций (§ 22).

Скорость роста концентрации D все время положительна: [D] монотонно возрастает от 0 до a. Продифференцируем третье уравнение системы (21.21)

иприравняем производную к нулю:

Вторая производная равна нулю в тот момент, когда концентрация интермедиата B максимальна. Это означает, что кинетическая кривая продукта D имеет S- образную форму с перегибом. До точки перегиба продукт D накапливается

Рис. 21.6. Зависимости концентраций веществ от времени в системе двух последовательных реакций первого порядка при k1 = 3 с−1, k2 = 15 с−1

a

A → B → D

[B]

k1 k2

k2 k1

t

Рис. 21.7. Зависимости концентрации промежуточного продукта от времени в системе двух последовательных реакций при различных соотношениях k1 и k2

с ускорением, а после нее скорость его образования постоянно уменьшается и стремится к нулю.

При малых временах концентрация продукта D настолько мала, что его нельзя обнаружить в системе. Время, в течение которого продукт практически отсутствует в системе, называют индукционным периодом. Его продолжительность зависит от чувствительности метода, применяемого для обнаружения вещества D.

Перейдем к количественному анализу. Точное решение системы (21.21) дает

При γ → 0 [B]max → a, а при γ → ∞ [B]max → 0. Это подтверждает качественные выводы о влиянии отношения констант скорости на максимально

возможную концентрацию интермедиата.

Если промежуточный продукт B неустойчив, т. е. k1 < k2, то через какое-то время слагаемым exp(−k2t) в уравнениях (21.22) можно пренебречь, тогда

т. е. отношение концентраций промежуточного продукта и реагента становится постоянным; такое состояние называют переходным равновесием. Если же

c/a

tg α = k1

α

t

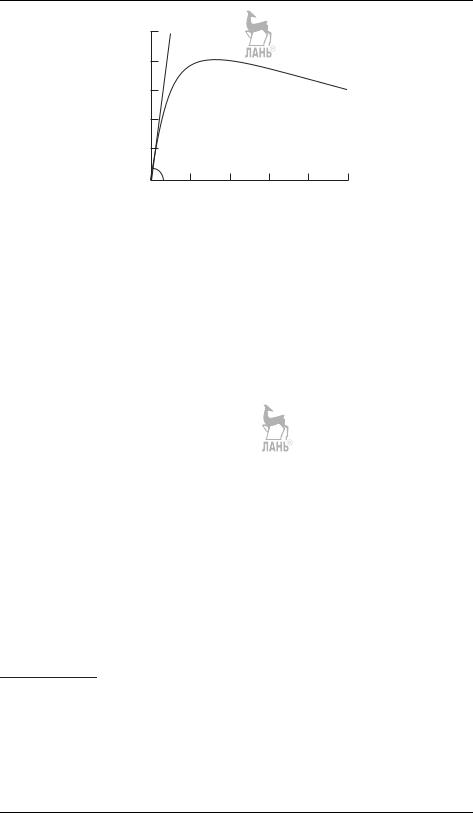
Рис. 21.8. Определение k1 из кинетической кривой (21.25)

первая константа скорости намного меньше второй, т. е. k1 k2, то в формуле (21.24.б) можно пренебречь величиной k1 в знаменателе, 1) что приводит к выражению

Это означает, что отношение концентраций промежуточного соединения и реагента равно отношению их периодов полураспада. Такое состояние называют вековым равновесием. Оно устанавливается при временах, много больших периода полураспада промежуточного соединения, t τ2.

Рассмотрим способы решения обратной задачи. Будем считать, что дана только кинетическая кривая, соответствующая промежуточному веществу B (обозначим его концентрацию c), а начальная концентрация реагента a известна. Необходимо найти константы скорости k1 и k2 по зависимости c(t):

Для определенности будем считать, что k1 > k2, т. е. первая реакция быстрая, а вторая — медленная. 2) При малых временах основное влияние на концентрацию оказывает константа скорости k1, так как вторая реакция еще не успевает

В координатах c/a – t начальные точки кинетической кривой ложатся на прямую, тангенс угла наклона которой равен k1 (рис. 21.8).

При больших временах быстрая реакция заканчивается (соответствующая экспонента e−k1t затухает) и концентрация определяется медленной стадией:

1) Обычно считают, что одним слагаемым можно пренебрегать по сравнению с другим, если они отличаются более чем на два порядка величины, т. е. в нашем случае k1/k2 <

<10−2.

2)Эта ситуация характерна для фармакокинетических моделей, где лекарства быстро всасываются в кровь и медленно превращаются в продукты метаболизма.