Неорганическая химия / Физическая химия / Еремин В.В., Каргов С.И., Успенская И.А., Кузьменко Н.Е., Лунин В.В. Основы физической химии. В 2-х ч. / Основы физической химии

220 Гл. IV. Статистическая термодинамика

дельных частиц:

причем интегрирование проводится по всему объему за вычетом собственного объема молекул: V1 = V − Nb.

Среднее поле рассчитывают, интегрируя потенциал парного взаимодействия (см. рис. 16.2, табл. 16.3) по всей области притяжения и умножая на плотность

От этого выражения берем натуральный логарифм и дифференцируем по объему:

Это и есть уравнение Ван-дер-Ваальса, в котором параметр a связан с амплитудой потенциала притяжения между молекулами, а параметр b характеризует объем, занимаемый одной молекулой.

Статистическая термодинамика адсорбции

Статистическая термодинамика позволяет находить уравнение состояния вещества не только в объеме, но и на поверхности. Рассмотрим адсорбцию идеального газа. Пусть на однородной поверхности находится N адсорбционных центров, из которых N1 заняты молекулами газа. Обозначим внутреннюю сумму по состояниям молекулы газа Qвн. Число распределений молекул газа по адсорбционным центрам равно

N!

N1!(N − N1)! .

Общая сумма по состояниям газа на поверхности равна произведению всех внутренних сумм по состояниям на число распределений (как в модели решеточного газа, но с той разницей, что частицы, фиксированные на поверхности, различимы; см. ч. 2, пример 16-3):

Найдем химический потенциал вещества на поверхности:

Fпов = −kT ln Zпов =

= −kT [N ln N − N1 ln N1 − (N − N1) ln(N − N1) + N1 ln Qвн] ,

где Θ — степень заполнения поверхности молекулами газа

Θ = NN1 .

Пусть в газовой фазе находится N2 молекул. Статистическая сумма газа:

N

Zгаз = [QпостQвн] 2 .

N2!

Найдем химический потенциал вещества в газовой фазе:

Fгаз = −kT ln Z = −kT [N2 ln Qпост + N2 ln Qвн − (N2 ln N2 − N2)] ,

При равновесии потенциалы вещества в газовой фазе и на поверхности равны:

Поступательная сумма прямо пропорциональна объему и, следовательно, обратно пропорциональна давлению, поэтому

где мы обозначили коэффициент пропорциональности KL.

Из соотношений (16.47) и (16.48) следует зависимость степени заполнения

Это изотерма адсорбции Ленгмюра (10.17.а). Из вывода видно, что внутренние степени свободы газа не влияют на уравнение адсорбции.

Мы рассмотрели только идеальные и некоторые простейшие неидеальные системы. На самом деле область применимости статистической термодинамики гораздо шире. Но и приведенных примеров достаточно, чтобы понять, как используя законы больших чисел статистическая теория позволяет связать внутреннее строение вещества с его термодинамическими свойствами и тем самым привести к гораздо более глубокому пониманию и обоснованию классической термодинамики.

Г л а в а V

ХИМИЧЕСКАЯ КИНЕТИКА

§ 17. Основные понятия химической кинетики

С помощью химической термодинамики можно определить направление любого химического процесса и его результат при заданных условиях. Термодинамика, однако, ничего не может сказать о том, осуществим ли практически данный процесс и за какое время он закончится. Например, смесь газообразных водорода и кислорода термодинамически неустойчива и должна самопроизвольно превращаться в воду, однако без внешнего воздействия и в отсутствие катализатора водород с кислородом практически не будут реагировать даже в течение миллионов лет. Время в химию вводит химическая кинетика — наука, предметом изучения которой служат изменяющиеся во времени системы.

Химическая кинетика — раздел физической химии, изучающий скорости и механизмы химических реакций.

Времена протекания химических реакций изменяются в огромном диапазоне — от 10−14 с до миллионов лет. Именно химическая кинетика позволяет определить, как быстро идет конкретная реакция в конкретных условиях и какие надо создать условия, чтобы она пошла быстрее, если реакция полезная, или медленнее, если реакция нежелательна.

Более конкретно, химическая кинетика с помощью своих экспериментальных и теоретических методов решает следующие основные задачи:

•измерение скорости реакции и выявление ее зависимости от условий эксперимента — температуры, концентраций веществ, давления;

•установление механизма химической реакции по экспериментальным данным и определение характеристик элементарных процессов, ее составляющих;

•установление связи между строением вещества и его реакционной способностью; неэмпирический расчет характеристик элементарных процессов.

Главная задача химической кинетики, как и химической термодинамики, —

построение модели химического процесса на основе экспериментальных данных. Однако для этого кинетика пользуется совсем другим языком. Основные различия между химической термодинамикой и кинетикой заключаются

вследующем.

1)В химической термодинамике нет переменной времени, она предсказывает только конечный результат процесса, а химическая кинетика изучает изменяющиеся во времени (динамические) системы.

2)Равновесные свойства определяются состоянием как исходных веществ, так и продуктов реакции. Для термодинамики важны левая и правая части

химического уравнения. Скорость элементарной реакции определяется только состоянием исходных веществ и условиями эксперимента. Для кинетики важна только левая часть уравнения реакции. 1)

3) При термодинамическом описании процесса оперируют активностями веществ, при кинетическом — их концентрациями.

Во многих сложных процессах, включающих обратимые реакции, кинетические и термодинамические характеристики оказываются тесно связанными друг с другом. В дальнейшем, там где это возможно, мы будем постоянно подчеркивать эту связь.

В определение химической кинетики входят два основных понятия — «скорость реакции» и «механизм реакции». Рассмотрим их подробно. Начнем со второго понятия, которое основано на определенной классификации химических реакций.

Химические реакции редко протекают именно так, как их описывает стехиометрическое уравнение, которое отражает лишь суммарный результат реакции и характеризует количественное соотношение между реагентами и продуктами. Почти все реакции включают сложную последовательность отдельных стадий. Как правило, кроме продуктов и реагентов в реакции участвуют также промежуточные вещества (интермедиаты), которые образуются из реагентов. Интермедиаты обычно неустойчивы и, реагируя как между собой, так и с реагентами, достаточно быстро превращаются в другие интермедиаты или в продукты. Так, реакция водорода с кислородом описывается простым суммарным

уравнением

2H2 + O2 = 2H2O,

но включает довольно много отдельных стадий:

H2 → 2H,

H + O2 → OH + O,

H + O2 → HO2,

O + H2 → OH + H,

OH + H2 → H2O + H,

Н + ОН → Н2О,

H + H + M → H2 + M и т. д.

Все эти реакции протекают с разными скоростями и вносят разный вклад в суммарный результат, однако для более полного кинетического описания надо учесть как можно большее число существенных стадий.

Одностадийные реакции, протекающие без образования интермедиатов, называют элементарными. Реакции, включающие две или более элементарных стадий, считают сложными. По стехиометрическому уравнению реакции нельзя определить, является она элементарной или сложной. Для этого требуется тщательный кинетический анализ.

Механизм реакции — это совокупность элементарных реакций, которые реализуют стехиометрическое превращение реагентов в продукты. Многие ре-

1)Исключение составляют автокаталитические реакции, скорость которых зависит

иот концентрации продукта.

акции включают всего 2–3 элементарные стадии, хотя существуют реакции, состоящие из нескольких десятков стадий.

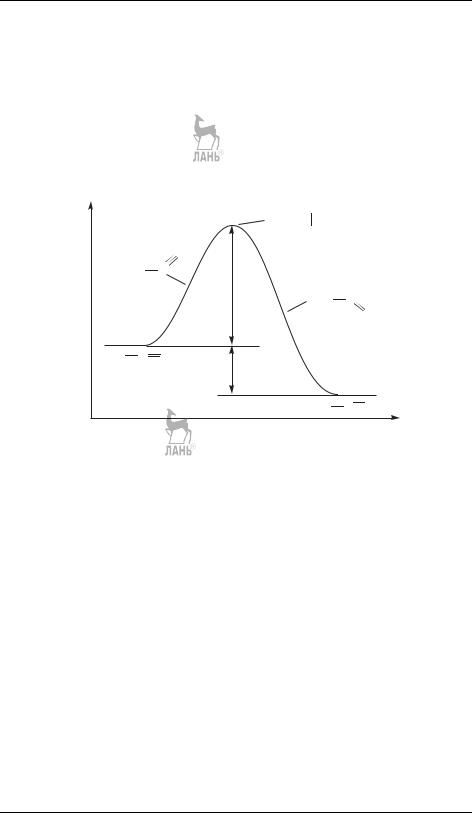
Существует более строгое определение элементарной реакции, основанное на рассмотрении энергетической кривой химической реакции (см. § 25). Химическая реакция начинается с разрыва химических связей в молекулах реагентов, что требует затраты энергии, поэтому между реагентами и продуктами всегда существует энергетический барьер (или несколько барьеров). Конфигурацию ядер вблизи этого барьера называют переходным состоянием между реагентами и продуктами (синонимы — переходный комплекс, активированный комплекс) (рис. 17.1).

Рис. 17.1. Энергетическая кривая реакции изомеризации метилизоцианида. Ea — энергия активации, H — тепловой эффект реакции

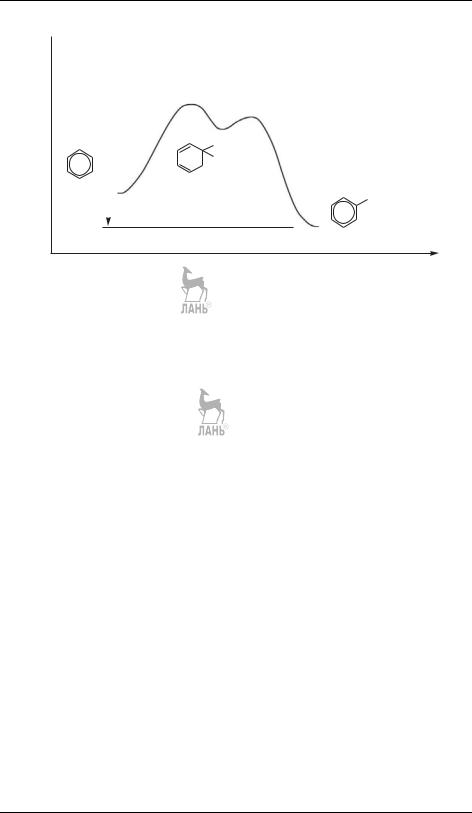
Элементарная реакция — это единичный акт образования и (или) разрыва химической связи, протекающий через образование переходного комплекса. Ей соответствует единственный максимум на энергетической кривой. Сложные реакции имеют несколько максимумов (рис. 17.2).

Число частиц, участвующих в элементарной реакции, называют молекулярностью реакции. Элементарные реакции бывают только трех типов.

1) Мономолекулярные реакции — элементарные реакции распада и изомеризации, в которых участвует только одна молекула:

X + YZ

XYZ → [X- - -Y- - -Z] → XY + Z реагент переходное X + Y + Z

состояние

продукты

Разрыв связей в исходной молекуле происходит под действием света или при нагревании, например:

hν

CH3Br −→ CH3 + Br.

кул (или числа молей n) этого вещества в единицу времени в единице объема:

Знак плюс используют, если скорость определяют по продукту, а минус — если по исходному веществу. Если реакция протекает при постоянном объеме, то скорость по веществу выражают через молярную концентрацию: c = n/V . 1)

Общую скорость реакции можно выразить через скорость по любому веществу, используя стехиометрические коэффициенты, которые связывают между собой количества реагентов и продуктов. Так, для реакции

νiAi → νj Aj

i j

для любых i и j. Стехиометрические соотношения между веществами дают возможность описать протекание реакции с помощью одной-единственной величины — химической переменной ξ (см. § 4), поэтому общую скорость реакции можно выразить через производную этой величины по времени:

Понятие «общая скорость реакции» строго определено только для элементарных процессов. Для сложной реакции, включающей ряд промежуточных стадий и/или побочных процессов, не описываемых стехиометрическим уравнением, значения скорости реакции, определенные по разным веществам, могут не совпадать друг с другом, и тогда понятие «скорость реакции» не имеет четкого смысла, можно говорить только о скорости по конкретному веществу (см. далее).

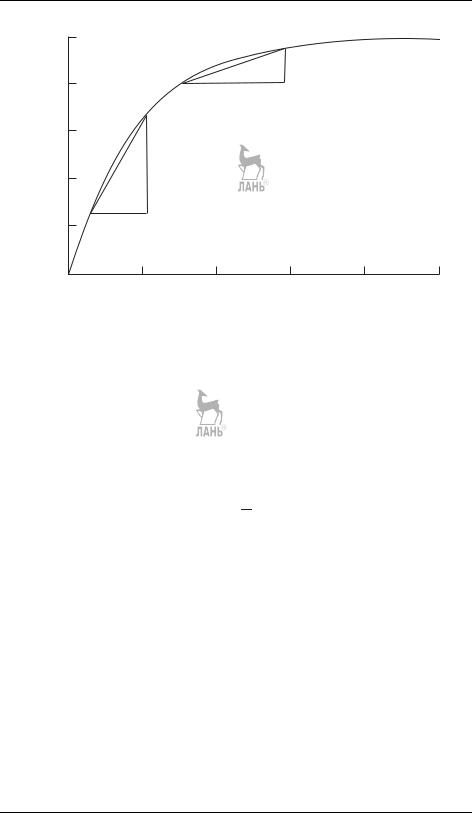
На практике среднюю скорость за время t часто определяют через конечные разности, например (рис. 17.3):

Для реакций, протекающих в газовой фазе, концентрация вещества прямо пропорциональна парциальному давлению, поэтому скорость можно выражать также через давления. Скорость реакции — размерная величина; ее типичные размерности: моль · л−1 · с−1, моль · см−3 · с−1, Па · с−1 и др.

Обратите внимание, что скорость реакции не остается постоянной в течение реакции: обычно она больше всего в начале и близка к нулю в конце реакции, когда реагентов уже почти не осталось.

Многие практически важные химические реакции протекают в промышленных реакторах, работающих в режиме потока газа. В этом случае объем газов не является постоянным и скорость реакции определяется наиболее общим выражением (17.1.а). Рассмотрим некоторые особенности реакций в потоке на примере реакции

1) Во многих учебных изданиях, включая настоящее, молярную концентрацию обозначают также квадратными скобками: cA ≡ [A].

концентрации: объему, давлению, электропроводности, электродному потенциалу, оптической плотности, сигналам ЯМР или ЭПР. Если в реакции участвуют оптически активные вещества, то их концентрацию можно определить по углу оптического вращения. Именно так немецкий химик Л. Вильгельми в 1850 г. впервые в истории химии измерил скорость реакции. Он изучал скорость реакции гидролиза сахарозы и нашел зависимость концентрации сахарозы от времени.

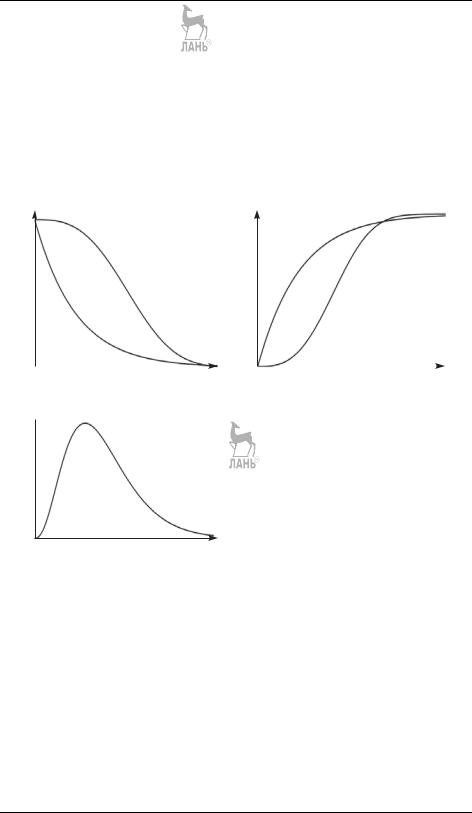
Измеряя зависимость концентрации от времени, c = f(t), получают кинетические кривые. Несмотря на большое разнообразие химических реакций, число принципиально различных кинетических кривых невелико — их основные типы приведены на рис. 17.4.

c

t

в

Рис. 17.4. Типичные кинетические кривые для реагентов (а), продуктов (б), интермедиатов (в)

Кинетические кривые можно рассчитать теоретически, используя законы и принципы химической кинетики. К ним относятся закон действующих масс, принцип независимости химических реакций, принцип лимитирующей стадии, принцип детального равновесия. Рассмотрим подробно первые два из них, а к остальным обратимся позднее, по ходу изложения.

Закон действующих масс

Скорость реакции в общем случае зависит от многих факторов — природы реагирующих веществ, их концентрации, температуры, наличия катализатора.

Зависимость скорости реакции от концентрации описывается основным постулатом химической кинетики — законом действующих масс:

Скорость элементарной реакции пропорциональна произведению текущих концентраций каждого из реагентов в степенях, равных молекулярности по данному веществу.

Для элементарной реакции νiAi → νj Aj

ij

Коэффициент пропорциональности k называют константой скорости реак-

ции. Для элементарных реакций k зависит только от температуры. Показатель

степени νi называют порядком реакции по i-му веществу, а сумму νi — об-

i

щим порядком реакции. Для элементарной реакции порядок по веществу равен стехиометрическому коэффициенту, а общий порядок равен молекулярности.

Формулы вида (17.9.а), выражающие зависимость скорости реакции от концентраций, называют кинетическими уравнениями. Это — точные уравнения, так как для элементарных реакций закон действующих масс выполняется строго. Решая численно или аналитически системы таких уравнений, находят теоретические кинетические кривые — это необходимо для решения обратной кинетической задачи (см. далее).

Закон действующих масс сформулировали в 60-х гг. XIX в. на основании экспериментальных исследований норвежские ученые — математик К. Гульдберг и химик П. Вааге. Они изучали обратимые реакции и, анализируя выражение для константы равновесия, предложили связать скорость прямой и обратной реакций с действующими массами (так в то время называли концентрации) реагирующих веществ. 1)

В зависимости от молекулярности элементарной реакции закон действующих масс может иметь следующий вид:

r= kcX (мономолекулярные реакции);

r= kcXcY или r = kc2X (бимолекулярные реакции);

r= kcXcYcZ или r = kc2XcY, r = kcXc2Y,

r= kc3X (тримолекулярные реакции).

Усложных реакций четко можно определить только скорость реакции по веществу. Для этого используют принцип независимости химических реакций:

Если в системе протекает несколько реакций, то каждая из них подчиняется основному постулату химической кинетики (17.9.а) независимо от других реакций.

При этом константа скорости каждой реакции не зависит от наличия остальных реакций, но текущая концентрация вещества рассчитывается с учетом всех реакций.

1)Интересно, что Гульдберг и Вааге опубликовали свою работу на норвежском языке

иона оставалась незамеченной научным сообществом до тех пор, пока через несколько лет ее не перевели на немецкий язык.