
Лекция Основные виды распределения случайной величины
.pdf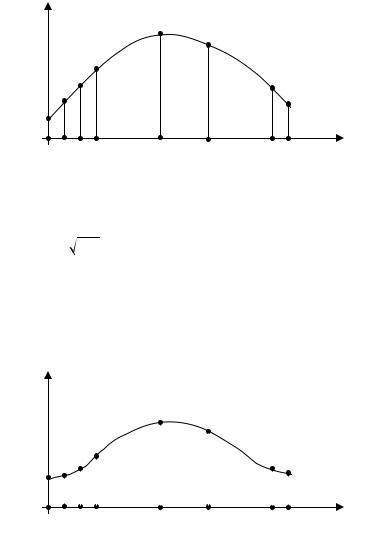
Основные виды распределения случайной величины
Наиболее часто применяемыми на практике являются следующие виды законов распределения: биномиальный, Пуассона (для дискретных случайных величин); равномерный, экспоненциальный, нормальный (для непрерывных случайных величин).
Определение 43. Биномиальным законом распределения называется закон, описывающий распределение вероятностей в схеме повторных независимых испытаний, определяемый формулой Бернулли:
Pn (k ) = Cnk pk qn−k .
P(X)
0 1 2 3 |
… M(X) … k |
… |
n-1 n |
X |
Рис. 3. Многоугольник биноминального распределения |
|
|||
Теорема 19. Для случайной |
величины Х, |
распределенной по |
биномиальному закону, |
|
M ( X ) = np; D( X ) = npq; ( X ) = 
 npq.
npq.
Определение 44. Распределением Пуассона называется закон, описывающий распределение вероятностей маловероятных событий (р мало) среди большого числа испытаний (n велико), причем
n p = = const : P (k ) = k e− .
n |
k ! |
|
P(X)
0 1 2 3 … M(X) … k … n-1 n |
X |
Рис. 4. Многоугольник Пуассоновского распределения
Теорема 20. Для случайной величины Х, распределенной по закону Пуассона, математическое ожидание и дисперсия равны параметру .
Определение 45. Случайная величина Х называется распределенной по равномерному закону, если ее
плотность на отрезке [a; b] постоянна, а вне его равна нулю:
0, |
|
x a, |
||
|
1 |
|
|
|
|
|
|
||
f ( x) = |
|
|
, a x |
b, |
|
− a |
|||
b |
x b. |
|
||
0, |
|
|
||
|
|
|
|
|
- 1 -
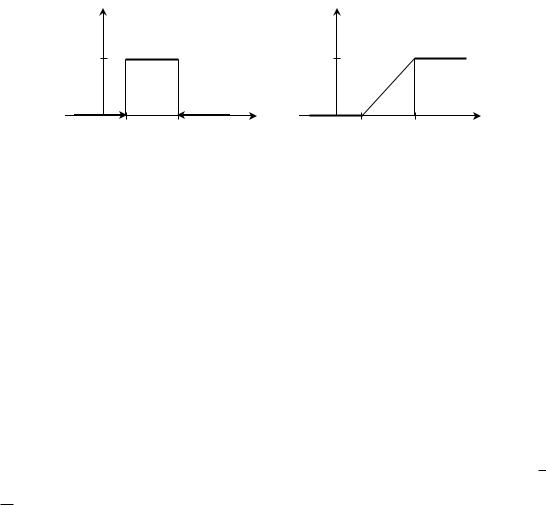
f (x)
1/(b – a)
0 а |
b |
x |
Рис. 5. Плотность равномерного распределения
Найдем F(x) для равномерного распределения:
F(x)
1
0 a |
b |
x |
|
Рис. 6. Функция распределения для равномерного распределения
|
x |
x |
1) |
Пусть x a, тогда F ( x) = |
f ( y)dy = 0dy =0; |
|
− |
− |
2) |
Пусть |
|
x
a x b, тогда F ( x) =
−
3) Пусть
d
f ( y)dy =
−
x |
d |
dy |
|
x − a |
|
|
f ( y)dy + |
f ( y)dy =0 + |
= |
; |
|||
b − a |
b − a |
|||||
− |
− |
|
|
|||
|
|
|
|
x |
|
|
|
a |
b |
x |
x b, тогда F ( x) = |
f ( y)dy = |
f ( y)dy + |
f ( y)dy + f ( y)dy =0 +1 + 0 = 1. |
|||
− |
|
|
|
− |
− |
− |
|
0, |
|
|
x a, |
|
|
|
|
− a |
|
|
|
|
|
x |
|
|
|
||
Следовательно: F ( x) = |
|
|
, |
a x b, |
|
|
|
− a |
|
||||
|
b |
|
x b. |
|
||
|
1, |
|
|
|
||
|
|
|
|
|
|
|
Теорема 21. Для случайной величины Х, распределенной по равномерному закону, M ( X ) = 12 (a + b) и
D( X ) = 121 (b − a )2 .
Определение 46. Случайная величина Х называется распределенной по экспоненциальному закону, если ее плотность вероятности равна
0, |
|
x 0, |
f ( x) = |
− x |
, x 0. |
e |
|
где > 0 – параметр экспоненциального распределения. Найдем F(x) для экспоненциального распределения:
xx
1)Пусть x 0, тогда F ( x) = f ( y)dy = 0dy =0;
|
|
|
− |
|
− |
|
2) Пусть |
|
|
|
|
|
|
x |
|
|
0 |
|
x |
|
x 0, тогда F ( x) = |
f ( y)dy = |
f ( y)dy + |
f ( y)dy = |
|||
− |
|
|
− |
|
− |
|
х |
|
x |
|
|
|
|
|
|
|
|
|
||
= 0 + e− y dy = −e− y |
= 1− e− x . |
|
|
|||
− |
|
0 |
|
|
|
|
|
|
0, |
|
x 0, |
||
Следовательно: F ( x) = |
− e− x , |
|
Это вероятность отказа элемента за время х. |
|||
|
|
1 |
x |
0. |
||
|
|
|
|
|
|
|
- 2 -
|
|
|
|
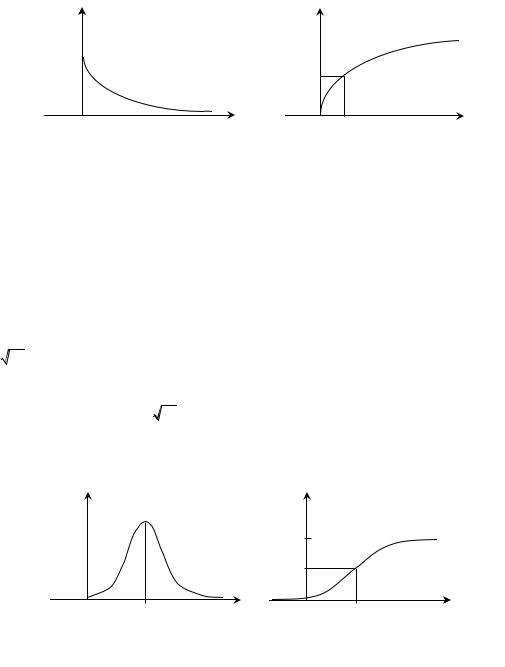
f (x) |
|
|
|
|
F(x) |
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1/2 |
|
|
|
|
x |
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
||||
0 |
Т0 |
||||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
Рис. 7. Плотность |
|
Рис. 8. Функция распределения |
|||||
|
|
|
|
экспоненциального |
|
экспоненциального распределения |
|||||
Замечание: Экспоненциальному закону подчинено время распада атомов различных элементов, а число |
|||||||||||
1/ = T носит название среднего времени распада. |
Кроме этого, число T0 = ln 2 / называют периодом |
||||||||||
полураспада, то есть это время, в течение которого распадается половина имеющегося вещества.
Теорема 22. Для случайной величины Х, распределенной по экспоненциальному закону,
M ( X ) = 1/ , D( X ) = 1/ 2 .
Определение 47. Случайная величина Х называется распределенной по нормальному закону, если ее
плотность вероятности равна
|
|
1 |
|
e− |
( x−a )2 |
|
|
|
f (x) = |
|
|
2 2 , |
где a, 0 – параметры нормального распределения. |
||||
|
|
|
|
|||||
|
|
2 |
||||||
|
|
|
|
|
|
|
||
Функция распределения случайной величины, распределенной по нормальному закону, имеет вид
F(x) = |
x − a |
+ |
1 |
, где 0 |
(x) = |
|
1 |
|||
0 |
|
|
2 |
|
|
|||||
|
|
|||||||||
2 |
||||||||||
|
|
|
|
|
|
|
||||
0 (−х) = −0 (х). (см. Приложение 3).
f (x)
0 M(x)
x |
− |
t2 |
|
|
|
e |
2 dt |
– функция Лапласа, значения которой табулированы, причем |
|||
|
|||||
0 |
|
|
|
|
|
|
|
F(x) |
|
|
1 |
|
|
|
1/2 |
|
|
x |
0 |
M(x) |
x |
|
|
Рис. 9. Плотность нормального |
Рис.10. Функция распределения |
|||||
|
|
|
распределения |
нормального распределения |
||
Теорема 23. Для случайной величины Х, распределенной по нормальному закону, М(Х) = а, D(Х) = 2. |
||||||
Теорема 24. Вероятность того, что нормально распределенная случайная величина попадет в интервал [ ; |
||||||
], равна |
|
|
|
|
|
|
|
− a |
|
− a |
|
||
P( X ) = 0 |
|
|
−0 |
|
. |
|
|
|
|||||
|
|
|
|
|
||
Замечание: Из последней теоремы видно, что P(a − X a + ) = 2 0 ( / ). В частности, если равно |
||||||
трем средним квадратическим отклонениям, то |
P(a −3 X a +3 ) = 2 (3) 0,997. Почти все значения |
|||||
нормальной случайной величины попадают в интервал [a −3 ; a +3 ] почти наверняка. Этот факт называют
«правилом трех сигм».
Пример 39. Все значения равномерно распределенной случайной величины лежат на интервале [1, 9]. Найти вероятность попадания случайной величины в интервал [3, 5].
- 3 -
|
|
|
|
|
|
|
|
|
0, |
x 1, |
Решение. По определению плотности равномерного распределения имеем |
|
1 x 9, тогда |
||||||||
f (x) = 1/ 8, |
||||||||||
|
|
|
|
|
|
|
|
|
|
x 9; |
|
|
|
|
|
|
|
|
|
0, |
|
5 |
dx |
|
5 |
|
3 |
|
1 |
|
|
|
P(3 X 5) = |
|
= |
|
− |
|
= |
|
. |
|
|
8 |
8 |
8 |
4 |
|
|
|||||
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Пример 40. Книга в 1500 страниц имеет 150 опечаток. Найти вероятность того, что на случайно выбранной странице не менее четырех опечаток.
Решение. В данной ситуации случайная величина распределена по закону Пуассона: = 150/1500 = 1/10.
|
|
|
(1/10) |
k |
1 |
|
|
|
|
|
e− |
|
. Искомая вероятность и вероятность найти менее четырех опечаток в сумме дают |
||||
Имеем P (k ) = |
|
10 |
||||||
|
|
|||||||
n |
|
|
k ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
единицу как вероятности противоположных событий. Следовательно, Риск.= 1 – |
(Р1000(0) + Р1000(1) + Р1000(2) + |
|||||||
Р1000(3)) = 1 – (0,904837+ 0,090483 + 0,004524 + 0,000151) 0,000004. |
|
|||||||
Пример 41. |
|
Непрерывная случайная величина распределена по |
экспоненциальному закону |
|||||
0, |
|
|
|
|
x 0, |
|
||
F ( x) = |
−3x |
, |
|
|
x 0. |
|
||
3e |
|
|
|
|
||||
Найти вероятность попадания в интервал [0,5; 0,9].
0,9 |
0,9 |
Решение. P(0,5 X 0, 9) = 3e−3x dx = −e−3x |
= −0, 067206 + 0, 22313 0,155924. |
0,5 |
0,5 |
- 4 -
