5.2 Моделирование процессов функционирования систем массового обслуживания как марковских процессов.

5.2.1 Смо замкнутого типа

Рассмотрим пример процесса, относящегося к схеме гибели и размножения: двое рабочих ремонтируют четыре станка, причем каждый рабочий занят ремонтом одного станка. Аналитическая модель данной системы массового обслуживания была рассмотрена в главе 3, а размеченный граф переходов представлен на рисунке 3.4.

Рассмотрим моделирование системы по принципу .

Система может находиться в пяти различных состояниях и переходы между состояниями происходят при возникновении событий: «в станке возникла неисправность» или «рабочий отремонтировал станок». Обозначения состояний аналогичны обозначениям, введенным в главе 3 при описании схемы гибели и размножения: S0 – все станки в рабочем состоянии, рабочие свободны; S1 – один станок неисправен и один рабочий занят его ремонтом; S2 –два станка неисправны и два рабочих заняты устранением неисправностей; S3 – неисправны три станка, все рабочие заняты и один станок ожидает наладки; S4 – сломаны все станки, все рабочие заняты и два станка ожидают, когда рабочие освободятся и наладят их. Время возникновения неполадок в станке и время, требуемое рабочему для его ремонта случайные величины, значения которых генерируется с помощью случайной величины, распределенной по экспоненциальному закону. Примем, что по умолчанию, все станки исправно функционируют и все рабочие свободны, т.е. система находится в состоянии S0. SF-диаграмма системы представлена на рисунке 5.8.

Рис. 5.8 SF-диаграмма для примера ремонта двумя рабочими четырех станков.

Общая SIMULINK-схема представлена на рисунке 5.9.

Рисунок 5.9 Simulink-схема

Для удобства наблюдения за функционированием системы выведены параметры, характеризующие состояние, в котором система находится в данный момент системного времени: L – число неисправных станков, n – число рабочих, занятых их наладкой. В данном случае в момент окончания функционирования системы сломан один станок и один рабочий занят его ремонтом (значения блока Display).

Процесс функционирования системы можно просмотреть в «смотровом» окне Scope (рис. 5.10).

Рис. 5.10 Процесс функционирования системы

Настройки данной SF-диаграммы выглядят следующим образом:

5.2.2 Смо циклического типа с ветвлением переходов

При реализации СМО с циклическим графом перехода (рис. 3.5), сначала строится общая схема в SIMULINK (рис. 5.12), а затем имитация процесса поломки-ремонта станка легко реализуется при помощи средства визуального моделирования STATEFLOW (рис. 5.11).

По сути рассматривается два основных состояния станка: On – станок исправен и состояние Off – станок сломался и его требуется отремонтировать. Поломка станка – случайный процесс, поэтому переход из состояния On в состояние Off происходит по истечению некоторого интервала времени, значение которого генерируется по экспоненциальному закону в блоке On. В системе различают три вида поломок в станке, в зависимости от трудоемкости процесса ремонта. Для этого в блоке Off введен параметр, который и определяет степень неисправности.

В нашем примере с вероятностью 0.5 неисправность станка незначительна и легко исправляется, с вероятностью 0.3 неисправность средней степени и для ее ремонта требуется больше времени, чем в первом случае, и с вероятность 0.2 станку требуется капитальный ремонт. В зависимости от вида неисправности из состояния Off осуществляется переход в состояния Rem3, Rem2, Rem1, соответственно. Это легко реализуется при помощи случайного параметра p с равномерным распределением на интервале (0, 1). Как только ремонт закончен, т.е. случайное время q отведенное на ремонт прошло, происходит переход в состояние On, т.е. станок опять нормально функционирует. Примем, что по умолчанию, станок находится в состоянии On.

Аналитическая модель данной системы была описана в главе 3. На ее основе строится SF-диаграмма, которая наглядно имитирует работу системы (рис. 5.11).

Рисунок 5.11 SF-диаграмма для примера ремонта станка

В этой задаче также нас интересует состояние станка, в каждый из моментов времени работы систем, а также состояние, в котором система находиться в конечный момент времени. Эту информацию мы можем наблюдать при помощи стандартных блоков SIMULINK (рис. 5.12). В данной реализации процесса, в конечный момент времени станок находится в ремонте, причем неисправность средней степени тяжести (это можно пронаблюдать в окне STATEFLOW, состояние, в котором находится система, выделено жирным – при данном запуске это Rem2 или в окне SIMULINK по значению блока Display – оно равно 2).

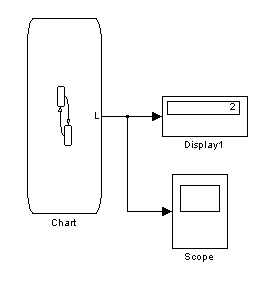
Рисунок 5.12 Simulink-схема для примера ремонта станка

Процесс функционирования системы, по окончанию ее работы, просматривается в блоке Scope (рис. 5.13).

Рис. 5.13 Процесс функционирования системы

Настройки данной SF-диаграммы, выглядят следующим образом (рис. 5.14):

Рисунок 5.14 Настройки диаграммы для примера ремонта станка