
- •Аннотация
- •1.Основные понятия теории моделирования
- •1.2 Определение абстрактной системы по р. Калману
- •Где –упорядоченное по возрастанию множество моментов времени,
- •1.3 Классификация систем по типу поведения
- •1.4 Принципы моделирования
- •2. Основы технологии имитационного моделирования
- •1.2 Аналитическое и имитационное моделирование
- •2.2 Понятие статистического эксперимента
- •2 .3 Область применения имитационных моделей
- •2.4 Управление модельным временем
- •2.5 Оценка качества имитационной модели
- •3. Типовые математические схемы моделей систем
- •3.1.2. Системы разностных уравнений.
- •3.1.3. Примеры систем, описываемых в классе d – схем
- •3.2 Дискретно-детерминированная модель. Конечные автоматы
- •3.3 Дискретно-стохастическая модель. Вероятностный автомат
- •3.4 Марковский процесс с дискретным временем перехода. Уравнения для вероятностей состояний.
- •3.5 Непрерывно-стохастическая модель. Потоки случайных событий.
- •3.6. Марковские процессы с непрерывным временем. Дифференциальные уравнения относительно вероятностей состояний.
- •3.5. Процессы в системах массового обслуживания как непрерывные
- •3.6, Непрерывно-стохастическая модель. Системы массового обслуживания.
- •3.7 Обобщенные модели
- •4. Описание программных средств визуального моделирования системы matlab
- •4.1 Некоторые сведения о пакете matlab
- •4.2 Краткая характеристика расширения matlab – simulink.
- •4.3 Описание программного средства stateflow.
- •5. Разработка моделей средствами simulink-stateflow
- •5.1 Вероятностный автомат
- •5.2 Моделирование процессов функционирования систем массового обслуживания как марковских процессов.
- •5.2.1 Смо замкнутого типа
- •5.2.2 Смо циклического типа с ветвлением переходов
- •5.2.3 Смо смешанного типа
- •5.2.4 Смо смешанного типа с различными характеристиками каналов
- •5.3 Общая схема моделирования смо.
- •Заключение
3.5 Непрерывно-стохастическая модель. Потоки случайных событий.
В
системах, которые могут быть описаны в
классе
![]() -
схем, обычно принимают, что переход из
состояния в состояние совершается
мгновенно, а время перехода связывают
с тем, что происходит некоторое событие,
которое и определяет момент перехода,
а часто и входной сигнал. Последовательность
таких событий, происходящих одно за
другим в случайные, заранее не известные
моменты времени, называют потоком
случайных событий. Этот поток определяет
получаемую последовательность состояний
системы во времени. Если эти состояния
случайны, то говорят, что в физической
системе происходит случайный или
вероятностный процесс с непрерывным
временем и дискретным состоянием.
-
схем, обычно принимают, что переход из
состояния в состояние совершается
мгновенно, а время перехода связывают
с тем, что происходит некоторое событие,
которое и определяет момент перехода,
а часто и входной сигнал. Последовательность
таких событий, происходящих одно за
другим в случайные, заранее не известные
моменты времени, называют потоком
случайных событий. Этот поток определяет
получаемую последовательность состояний
системы во времени. Если эти состояния
случайны, то говорят, что в физической
системе происходит случайный или
вероятностный процесс с непрерывным
временем и дискретным состоянием.
Примерами потоков являются, например, поток обращений к сайту, поток машин на заправку, поток заявок на выполнение тех или иных работ и т.д.
Поток событий называется однородным, если он характеризуется только моментами наступления событий (вызывающие моменты) и задается последовательностью:
![]() (
0 ),
(
0 ),
где
![]() – момент наступленияn-ого
события – неотрицательное вещественное
число.
– момент наступленияn-ого
события – неотрицательное вещественное
число.
Например, если в соответствии с поставленной задачей не требуется различать типы самолетов, приземляющихся в аэропорту, то поток событий приземления можно рассматривать как однородный.
Однородный
поток может так же быть задан в виде
последовательности промежутков между
n-м
и (n-1)-м
событиями
![]() ,
которые однозначно связаны с
последовательностью вызывающих моментов
,
которые однозначно связаны с
последовательностью вызывающих моментов![]()
![]() ;
; ![]() ,
,![]() ,
,![]() .
.
Последовательность![]()
![]() -
последовательность случайных положительных
(неотрицательных) чисел.
-
последовательность случайных положительных
(неотрицательных) чисел.
Потоком
неоднородных
событий
называется последовательность![]() ,
где
,
где![]() - набор признаков события (например, тип
самолета).
- набор признаков события (например, тип
самолета).
Если
интервалы
![]() ;
;![]() независимые случайные числа – поток
событий называютпотоком
с ограниченным последействием, или
потоком Пальма.
независимые случайные числа – поток
событий называютпотоком
с ограниченным последействием, или
потоком Пальма.
Поток
событий называется ординарным,
если вероятность того, что на малый
интервал времени
![]() ,
примыкающий к моментуt,
попадает больше одного события,
пренебрежимо мала по сравнению с
вероятностью того, что на этот же интервал
времени
,
примыкающий к моментуt,
попадает больше одного события,
пренебрежимо мала по сравнению с
вероятностью того, что на этот же интервал
времени![]() попадет не более одного события.
попадет не более одного события.
Пусть
вероятности
![]() ,
,![]() ,
,![]() есть вероятности того, что на интервал
есть вероятности того, что на интервал![]() соответственно событие не попадает,
попадает ровно одно событие и попадает
более одного события. Это вероятности
полной группы несовместных событий.
Тогда для ординарного потока можно
записать:
соответственно событие не попадает,
попадает ровно одно событие и попадает
более одного события. Это вероятности
полной группы несовместных событий.
Тогда для ординарного потока можно
записать:
![]() ;
(0)
;
(0)
![]() ;
(0)
;
(0)
![]() ;
(0)
;
(0)
где![]() -
величина порядка малости, выше
-
величина порядка малости, выше![]() т.е.
т.е.
 .
(0)
.
(0)
Среднее
число событий на интервале
![]() есть:
есть:
![]() ;
(0)
;
(0)
т.е.![]() при малых
при малых![]() численно равно среднему числу событий
на интервале.
численно равно среднему числу событий
на интервале.
Для ординарного потока событий:
![]() ,
( 0 )
,
( 0 )
(если этот предел существует);
![]() называется
интенсивностью (плотностью) потока.
Физически
называется
интенсивностью (плотностью) потока.
Физически
![]() среднее число событий в единицу времени.
Это неотрицательная функция времени,
имеющая размерность
среднее число событий в единицу времени.
Это неотрицательная функция времени,
имеющая размерность![]() .
.
Стационарным
потоком
событий называется поток, для которого
вероятность появления некоторого числа
событий на интервале, длинной
![]() ,
зависит лишь от длинны интервала и не
зависит от того, где на оси времени взят
этот интервал. Для такого потока=const.
(не зависит от времени). Экспериментальной
оценкой плотности потока может служить
отношение
,
зависит лишь от длинны интервала и не
зависит от того, где на оси времени взят
этот интервал. Для такого потока=const.
(не зависит от времени). Экспериментальной
оценкой плотности потока может служить
отношение
![]() ,
,
где
![]() -
число событий,
-
число событий,![]() -
интервал времени.
-
интервал времени.
Если
вероятность наступления
![]() событий в полуинтервале
событий в полуинтервале![]() не зависит от того, сколько событий
наступило в интервале [
не зависит от того, сколько событий
наступило в интервале [![]() ),
то поток называютпотоком
без
последействия
(с отсутствием последействия).
),
то поток называютпотоком
без
последействия
(с отсутствием последействия).
Простейшим потоком называют стационарный, ординарный поток без последействия.
Пуассоновский поток событий - это ординарный поток без последействия.
Если
на числовой оси взять два интервала
длинной
![]() и
и![]() ,
,![]() и
и![]() - числа событий на соответствующих
интервалах, то для потока без последействия
числа
- числа событий на соответствующих
интервалах, то для потока без последействия
числа![]() и
и![]() являются независимыми случайными
числами и
являются независимыми случайными
числами и![]() ;
где
;
где![]() .
Т.е. условная вероятность того, что
.
Т.е. условная вероятность того, что![]() при условии
при условии![]() равна безусловной вероятности того,
что
равна безусловной вероятности того,
что![]() .
.
Пусть
![]() -
вероятность того, что на отрезке длиной
с началом в момент времени
-
вероятность того, что на отрезке длиной
с началом в момент времени
![]() произойдет число событий
произойдет число событий![]() =
=![]() .
Эта вероятность для пуассоновского
потока событий определяется соотношением:
.
Эта вероятность для пуассоновского
потока событий определяется соотношением:
![]() ;
(0)
;
(0)
где a(t,)- среднее число событий на рассматриваемом интервале.
![]() .
(0)
.
(0)
Если пуассоновский поток – стационарный, то
![]() ;
(0)
;
(0)
и на участке длительностью наступит m событий с вероятностью:
![]() ;
(0)
;
(0)
т.е. простейший поток- это стационарный пуассоновский поток.
Найдем
закон распределения интервалов времени
![]() между двумя соседними состояниями.
между двумя соседними состояниями.

Рис. 1
Вероятность того, что на участке t не будет ни одного события:
![]() ;
( 0 )
;
( 0 )
но
![]() .
.
Тогда
функция распределения
![]() интервалов времени
интервалов времени![]() между событиями будет равна:
между событиями будет равна:
![]() ;
(
;
(![]() >0);
( 0)
>0);
( 0)
а плотность распределения имеет вид:
![]() .
( 0 )
.
( 0 )
Таким образом, интервалы времени между событиями в простейшем потоке распределены по закону (14), называемому экспоненциальным или показательным законом плотности распределения вероятностей.
Математическое
ожидание и дисперсия интервалов
![]() определяются соотношениями:
определяются соотношениями:
![]() ;
( 0 )
;
( 0 )
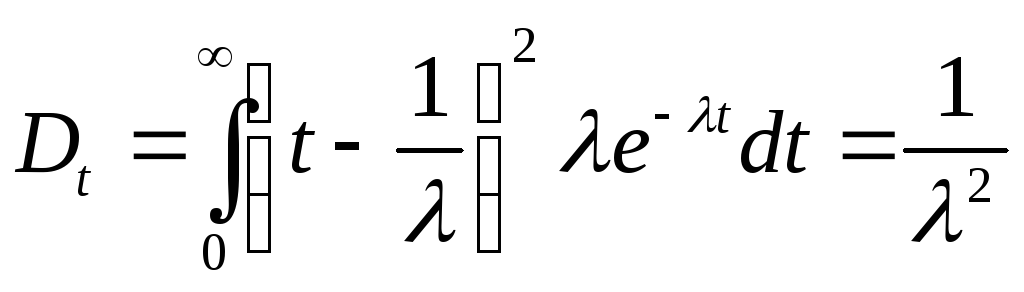 (
0 )
(
0 )
Если
интенсивность высока, то
![]() мало. Вообще говоря, если интервалы
распределены по одному и тому же законуf(z),
поток называют рекуррентным и среднее
значение интервала определяется обычной
формулой математического ожидания:
мало. Вообще говоря, если интервалы
распределены по одному и тому же законуf(z),
поток называют рекуррентным и среднее
значение интервала определяется обычной
формулой математического ожидания:
![]() .
.
![]() ( 0 )
( 0 )
Используются и другие виды потоков, например регулярный поток, т.е. поток, в котором моменты времени появления событий заранее определены, или потоки Эрланга различных порядков, формируемые на основе “просеивания” простейших потоков.
Рис. 2
Так,
поток Эрланга
к - го порядка
![]() – это поток, интервалы между событиями
в котором составляют суммуk+1-ой
независимых случайных величин,
распределенных по показательному
закону. Поток
– это поток, интервалы между событиями
в котором составляют суммуk+1-ой
независимых случайных величин,
распределенных по показательному
закону. Поток
![]() есть простейший поток. Потоки Эрланга
являются стационарными ординарными
потоками с ограниченным последействием.
есть простейший поток. Потоки Эрланга
являются стационарными ординарными
потоками с ограниченным последействием.
Главной характеристикой случайного потока является его интенсивность – своеобразная «скорость» появления событий.
