§ 1.2 Правило рунге.
Правило двойного пересчета. Правило практической оценки погрешности.
Пусть - приближенное значение интеграла, вычисленное по некоторой квадратурной формуле. Для погрешности квадратурной формулы справедливо представление:
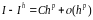(1.7)
Где
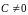и
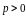- величины, не зависящие от h.Тогда
величина
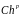называется
главным членом погрешности квадратурной
формулы. Отбросим члены более высокого
порядка малости, и будем считать, что
сделано два вычисления интеграла: с
шагом h
и h/2:
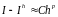
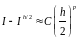
Вычитая из верхнего равенства нижнее, получим приближенное равенство:
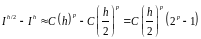
Учитывая приближенное равенство (), можно считать, что выведена формула,
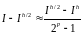(1.8)
называемая правилом Рунге или апостериорной оценкой погрешности.
Уточнение по Рунге
Приближенное равенство (1.6) позволяет получить уточненное значение интеграла:
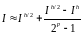(1.9)
Последняя формула называется уточнением по Рунге.
Замечание 1. Заменой h на 2h формула (1.9) приводится к следующему виду:
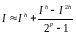
Замечание 2. Выполнение уточнения по Рунге для формулы трапеций приводит к формуле, совпадающей с формулой Симпсона. Действительно,
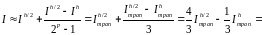
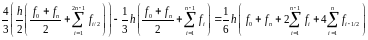
ПРИМЕРЫ.
Вычислить интеграл
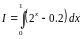по формуле трапеций.
Решение.
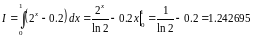
Вычислим значения подинтегральной функции в следующих точках:
f(0)=0.8 f(1/2)=1.414214-0.2=1.214214 f(1)=1.8
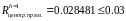
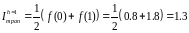
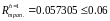
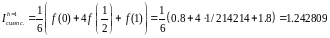
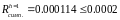
Продемонстрируем работу правила Рунге. Вычислим интеграл по формуле трапеций при уменьшенном вдвое шаге интегрирования.
-
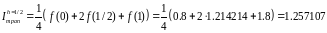
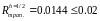погрешность уменьшилась примерно в 3
раза.
Рис.1.2. Схема алгоритма вычисления определенного интеграла
с автоматическим выбором шага интегрирования.
§ 1.3 Квадратурные формулы интерполяционного типа.
Рассмотренные
методы относятся к формулам Ньютона-Котеса.
Обобщим полученные результаты.
Зафиксируем некоторые значения
.
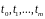
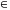
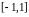Аппроксимируем функцию f(x)
на i-ом
элементарном отрезке
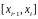интерполяционным многочленом
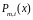с узлами интерполяции
,
.
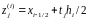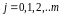Приближенная замена интеграла I
суммой
=
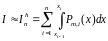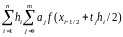(1)
приводит к составной формуле интерполяционного типа. Квадратурные формулы интерполяционного типа, построенные на основе равноотстоящих значений
называются формулами Ньютона-Котеса.
Приведем квадратурные формулы Ньютона-Котеса, отвечающие использованию многочленов степени m=1,2,3:
m=1
формула трапеций
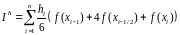m=2
формула Симпсона
, m=3
правило 3/8
Формула 6-го порядка точности:
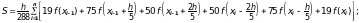
остаточный член
Учебник стр.430