
- •ВВЕДЕНИЕ В
- •1. Основные понятия теории графов
- •Ориентированный
- •Неориентированны
- •неориентированные
- •Основные понятия
- •Пути и циклы в графе
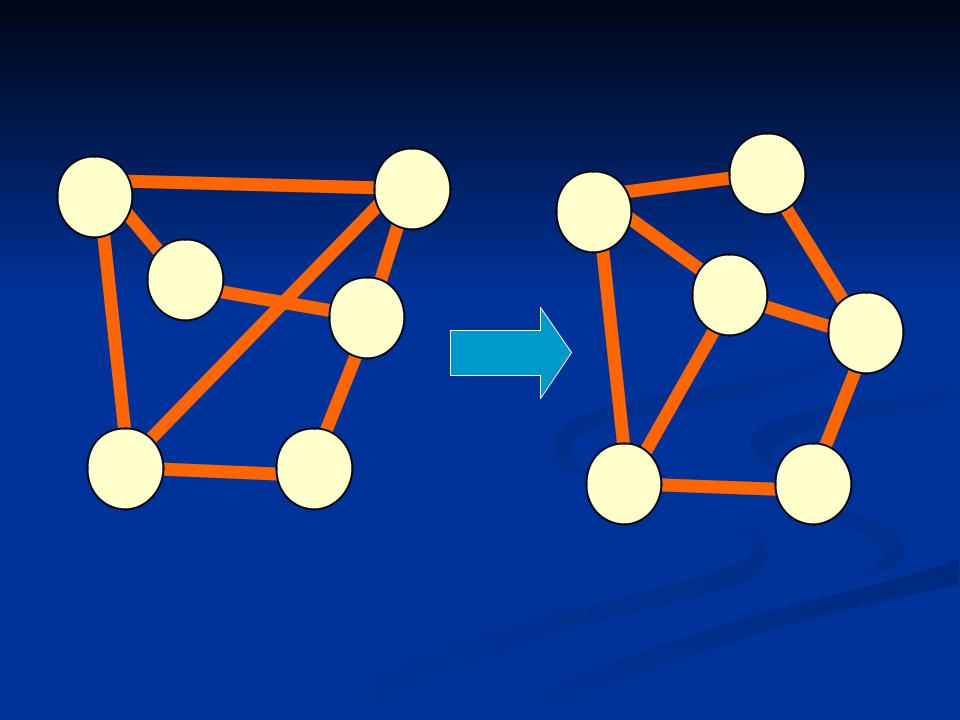
- •Изоморфизм графов
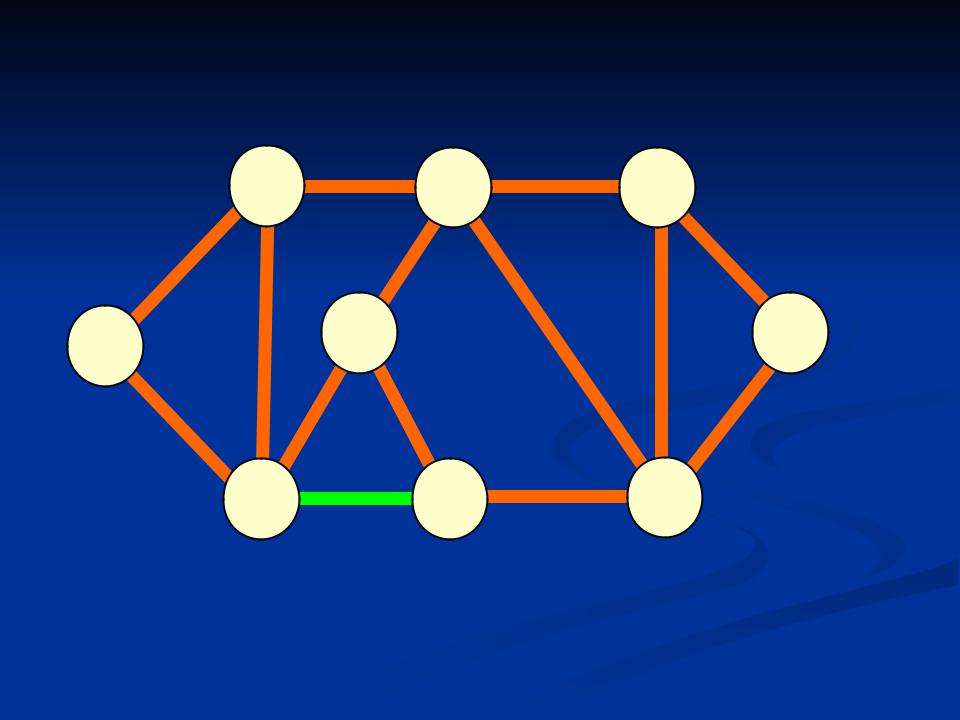
- •Подграфы
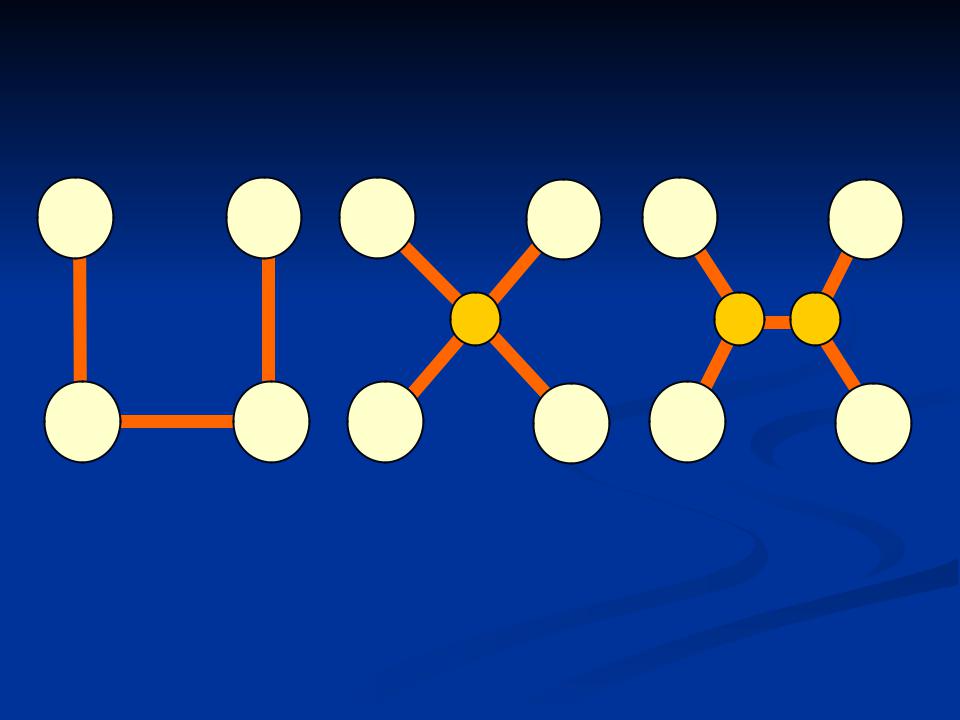
- •Клики в графе
- •Двудольные графы
- •Планарные и плоские
- •2. Алгоритмы на графах
- •Минимальные
- •Отличия теории и
- •Алгоритм Краскала
- •Алгоритм Краскала
- •Алгоритм Краскала
- •Алгоритм Краскала
- •Алгоритм Краскала
- •Алгоритм Краскала
- •Алгоритм Краскала
- •Алгоритм Краскала
- •Алгоритм Краскала
- •Алгоритм Краскала
- •Алгоритм Прима
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •Алгоритм Прима шаг
- •КРАТЧАЙШИЕ ПУТИ В ГРАФЕ
- •Алгоритм Дейкстры
- •Алгоритм Дейкстры
- •Алгоритм Дейкстры
- •Алгоритм Дейкстры
- •Алгоритм Дейкстры
- •Алгоритм Дейкстры
- •Алгоритм Дейкстры
- •Алгоритм Дейкстры
- •Алгоритм Дейкстры
- •Алгоритм А*
- •Оценка длины пути
- •Алгоритм А*
- •Алгоритм А*
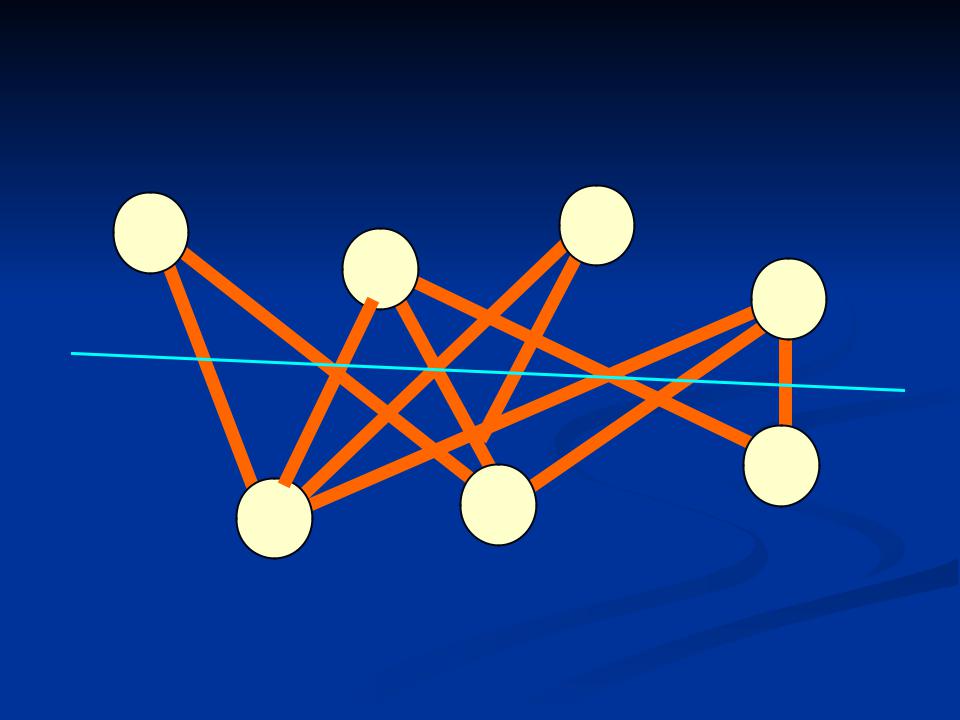
Двудольные графы
A E
D F
G
B C
Планарные и плоские
графы
A E
D
F
B C
Планарный
граф
D
A
E
F
B C
Плоский
граф

2. Алгоритмы на графах
Минимальные
покрывающие деревья
Имеется граф G(V,E)
Каждому ребру (u,v) задан неотрицательный вес w(u,v)
Задача: найти подмножество Т Е, связывающее все вершины, для которого минимален суммарный вес
w(T)= w(u,v)
(u,v)εT
Отличия теории и
практики
A А D A B D A C
B |
C B |
C B |
кратчайшее дерево:
А - без дополнительных вершин
В - с дополнительной
вершиной
С – дерево Штейнера
D
C

Алгоритм Краскала
шаг 0
B |
|
8 |
C |
7 |
D |
|
|
|
|||
4 |
|
|
2 |
4 |
9 |
A 11 |
|
I |
|
14 E |
|
7 |
|
|
|||
|
6 |
|
|
||
8 |
|
|
|
10 |
|
|
|
|
|
||
H |
|
1 |
G |
2 |
F |
|
|
|
|
Суммарная длина деревьев = 0
Алгоритм Краскала
шаг 1
B |
|
8 |
C |
7 |
D |
|
|
|
|||
4 |
|
|
2 |
4 |
9 |
A 11 |
|
I |
|
14 E |
|
7 |
|
|
|||
|
6 |
|
|
||
8 |
|
|
|
10 |
|
|
|
|
|
||
H |
|
1 |
G |
2 |
F |
|
|
|
|
Суммарная длина деревьев = 1
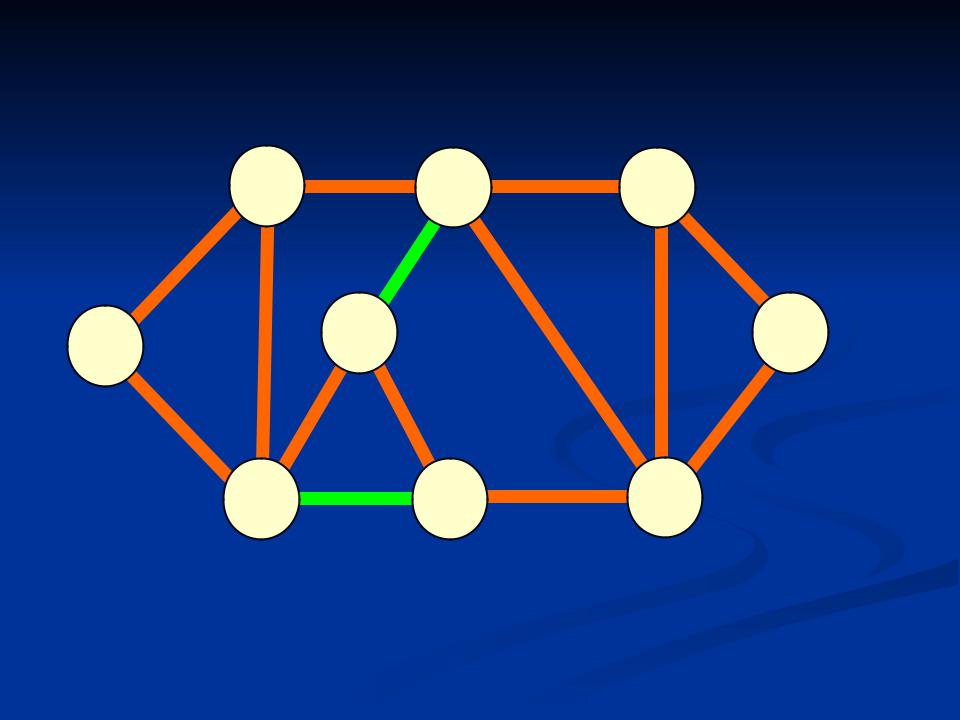
Алгоритм Краскала
шаг 2
B |
|
8 |
C |
7 |
D |
|
|
|
|||
4 |
|
|
2 |
4 |
9 |
A 11 |
|
I |
|
14 E |
|
7 |
|
|
|||
|
6 |
|
|
||
8 |
|
|
|
10 |
|
|
|
|
|
||
H |
|
1 |
G |
2 |
F |
|
|
|
|
Суммарная длина деревьев = 3
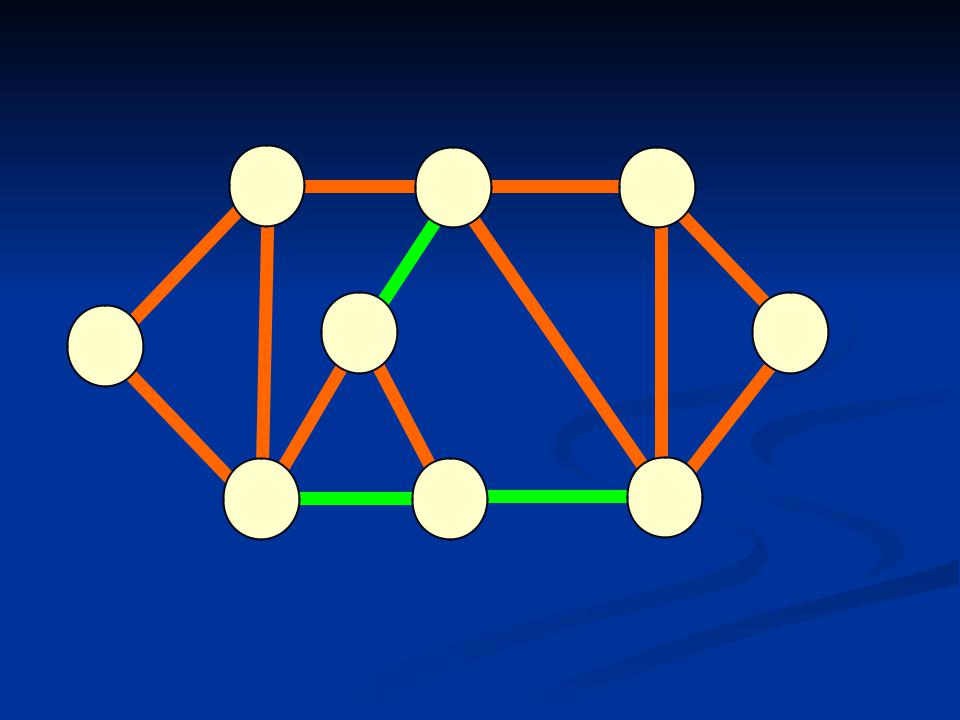
Алгоритм Краскала
шаг 3
B |
|
8 |
C |
7 |
D |
|
|
|
|||
4 |
|
|
2 |
4 |
9 |
A 11 |
|
I |
|
14 E |
|
7 |
|
|
|||
|
6 |
|
|
||
8 |
|
|
|
10 |
|
|
|
|
|
||
H |
|
1 |
G |
2 |
F |
|
|
|
|
Суммарная длина деревьев = 5

Алгоритм Краскала
шаг 4
B |
|
8 |
C |
7 |
D |
|
|
|
|||
4 |
|
|
2 |
4 |
9 |
A 11 |
|
I |
|
14 E |
|
7 |
|
|
|||
|
6 |
|
|
||
8 |
|
|
|
10 |
|
|
|
|
|
||
H |
|
1 |
G |
2 |
F |
|
|
|
|
Суммарная длина деревьев = 9
