Десятичные сумматоры
Для
построения многоразрядных двоичных
сумматоров, как было показано выше,
необходимы одноразрядные двоичные
сумматоры строятся с использованием
одноразрядных десятичных сумматоров.
Последние выполняют операцию суммирования
.десятичных цифр
,
и
переноса
,
поступающих в разряд, и формируют на
выходах десятичную цифру суммы
и
перенос
для
передачи в следующий десятичный разряд.
При использовании десятичной системы счисления цифры разрядов десятичного числа представляются в некоторой двоичной форме (см. § 3.2). В связи с этим одна из особенностей одноразрядных десятичных сумматоров связана с тем, что суммируемые Десятичные цифры и представляются многоразрядными двоичными числами (переносы независимо от используемой системы счисления могут иметь лишь значения 0 либо 1). Рассмотрим построение одноразрядного сумматора десятичных цифр, представляемых в коде 8421.
Сумматор для кода 8421.
В работе сумматора этого типа имеются особенности в формировании переноса и суммы, отличающие его от работы двоичного сумматора.
Правила
сложения в десятичной системе счисления
с использованием кода
8421 рассмотрены
в § 3.3. Построенная в соответствии с
этими правилами схема одноразрядного
десятичного сумматора (рис. 9.67) включает
в себя четырехразрядный двоичный
сумматор(1),
схему формирования переноса
в
следующий десятичный разряд (2) и схему
коррекции суммы (3). Последняя представляет
собой трехразрядный сумматор, в котором
при
производится
прибавление единицы в разрядах
нескорректированной суммы с весовыми
коэффициентами 2 и 4.
Операция суммирования в случае, когда слагаемые (одно либо оба) имеют отрицательные значения, может производиться с представлением таких слагаемых в обратном коде.
Схема формирования обратного кода.
В десятичной системе счисления обратный код образуется путем преобразования каждой цифры числа в дополнение до 9. В табл. 9.35 приведены для десятичных цифр 0, 1,…, 9 прямые коды и соответствующие им обратные.
рис 9.67
Из
сопоставления приведенных в таблице
значений
и
соответствующих им
нетрудно
заключить, что
.
Таблица 9.35 |
||||||||
Десятичная ячейка |
Прямой код 8421 |
Обратный код |
||||||
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
3 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
5 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
6 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
7 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
8 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
9 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
Логические
выражения для
и
можно
получить из карт Вейча (табл. 9.36):
;
.
На рис. 3,68 приведена схема, формирующая обратный код по полученным выше логическим выражениям,
Таблица 9.36 |
|
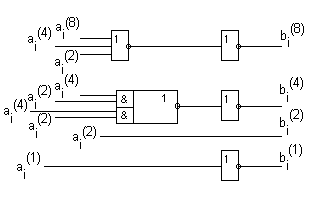
рис 9.68
рис 9.69